Бета-розподіл
Бе́та-розпо́діл в теорії імовірностей та статистиці — двопараметрична сім'я абсолютно неперервних розподілів.
| Бета-розподіл | |
|---|---|
|
Функція ймовірностей  | |
|
Функція розподілу ймовірностей 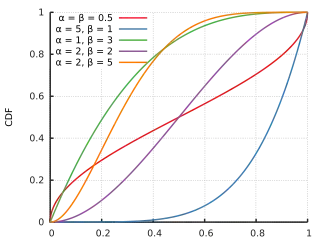 | |
| Параметри |
|
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Мода | для |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Твірна функція моментів (mgf) | |
| Характеристична функція | |
Означення
Нехай розподіл випадкової величини задаєтся густиною ймовірності , що має вигляд:
- ,
де
- довільні фіксовані параметри, і
- — бета-функція.
Тоді випадкова величина має бета-розподіл. Пишуть: .
Форма графіка
Форма графіка густини ймовірності бета-розподілу залежить від вибору параметрів і .
- — графік опуклий і прямує до нескінченності на границях (червона крива);
- чи — графік строго спадний (синя крива)
- — графік строго опуклий;
- — графік є прямою лінїєю;
- — графік строго ввігнутий;
- графік збігається з графіком густини стандартного неперервного рівномірного розподілу;
- або — графік строго зростаючий (зелена крива);
- — графік строго опуклий;
- — графік є прямою линією;
- — графік строго ввігнутий;
- — график унімодальний (пурпурова та чорна криві)
У випадку, коли , густина ймовірності симетична відносно (червона та пурпурова криві), то
- .
Моменти
Математичне сподівання та дисперсія випадкової величини , що має бета-розподіл, мають такий вигляд:
- ,
- .
Зв'язок з іншими розподілами
Стандартний неперервний рівномірний розподіл є окремим випадком бета-розподілу:
— незалежні гамма-розподілені випадкові величини, причому , а , то
Апріорний розподіл Голдейна
Розподіл B(0,0) запропонував Джон Бердон Сандерсон Голдейн,[1] який зауважив що апріорна ймовірність що представляє повну непевність повинна бути пропорційною до p−1(1−p)−1. Функцію p−1(1−p)−1 можна розглядати як границю бета розподілу в якому обидва параметри наближаються до нуля, α, β → 0. Таким чином, p−1(1−p)−1 розділена на бета-функцію наближається до двоточкового розподілу Бернуллі в якому вся густина розподілу сконцентрована на кінцях, в 0 і 1, у вигляді дельта-функції Дірака, і нульова між ними. Це приклад розподілу ймовірностей для підкидання монети, якщо одна сторона - нуль, а інша - 1.
Примітки
- Haldane, J.B.S. (1932). A note on inverse probability. Mathematical Proceedings of the Cambridge Philosophical Society 28: 55–61. doi:10.1017/s0305004100010495.