Виділення квадрату
В елементарній алгебрі виділення квадрату — це методика перетворення квадратного тричлена
до вигляду
де h і k — це деякі значення.
Виділення квадрату використовується при
- розв'язуванні квадратних рівнянь,
- при виведенні формули розв'язків квадратного рівняння,
- побудові графіків квадратичних функцій,
- оцінці інтегралів, наприклад, гаусових інтегралів з лінійною функцією в експоненті,
- пошуку перетворення Лапласа.
В математиці виділення квадрату часто використовується в різних обчисленнях із застосуванням квадратних тричленів.
Огляд
Уявлення
Формула з елементарної алгебри для обчислення квадрата двочлена:
Наприклад:
У будь-якому повному квадраті, коефіцієнт біля х у два рази перевищує число p, а вільний член дорівнює p2.
Простий приклад
Розглянемо наступний квадратний поліном:
Він не є повним квадратом, оскільки 28 не квадрат числа 5:
Однак, можна цей тричлен представити у вигляді суми повного квадрату і числа:
Це і називається виділенням повного квадрату.
Основний опис
Розглянемо довільний квадратний тричлен з коефіцієнтом при старшому члені 1 (нормований тричлен):
а також квадрат двочлена
Ці тричлени відрізняються тільки на сталу величину — в них різні вільні члени. Таким чином, ми можемо написати
де . Така операція називається виділенням квадрату. Наприклад:
Узагальнення основного опису
Розглянемо квадратний тричлен вигляду
Винесемо коефіцієнт при старшому члені за дужки, отримаємо випадок, описаний вище.
Приклад:
Це дозволяє нам представити довільний квадратний тричлен у формі
Скалярний вигляд
Для виділення повного квадрату можна використовувати формули. Для загального випадку:[1]
Зокрема, коли а = 1:
Матричний вигляд
Матричний вигляд дуже схожий:
де має бути симетричною.
Якщо не симетрична, формули і мають такий вигляд:
- .
Графічне представлення
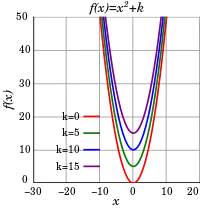
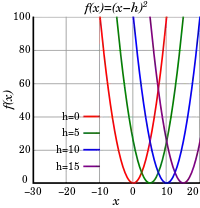
В аналітичній геометрії, графік будь-якої квадратичної функції є парабола в ху-площині. Враховуючи вигляд квадратного тричлена
числа h та k можуть бути інтерпретовані як декартові координати вершини параболи. Тобто, h — це х-координата осі симетрії (наприклад, вісь симетрії має рівняння х = h), і k — це мінімальне значення (або максимальне значення, Якщо а < 0) квадратичної функції.
Один зі способів переконатися у цьому — зверніть увагу, що графік функції ƒ(х) = х2 є парабола з вершиною в початку координат (0, 0). Таким чином, графік функції ƒ(x − h) = (x − h)2 є парабола зміщена вправо на h з вершиною в (h, 0), як показано у верхній частині малюнка. На відміну від попереднього графіка функції, ƒ(х) + k = x2 + k — це парабола зміщена вгору на k з вершиною в (0, k), як показано в центрі малюнка. Поєднання горизонтального і вертикального зміщень дає ƒ(x − h) + k = (x − h)2 + k, при якому парабола зсувається вправо на h і вгору на k з вершиною в (h, k), як показано на нижньому малюнку.
Розв'язування квадратних рівнянь
Виділення квадрату може бути використане для розв'язання будь-якого квадратного рівняння. Наприклад:
Виділимо повний квадрат:
Звідси маємо, що:
Тому
і тому
Це може бути застосовано до будь-якого квадратного рівняння. Коли коефіцієнт при х2 відмінний від 1, першим кроком є поділ на рівняння на цей коефіцієнт.
Ірраціональні і комплексні корені
На відміну від методів, пов'язаних з розкладанням рівняння на множники, яке є надійним, тільки якщо корені раціональні, виділенням квадрату знайдемо корені квадратного рівняння навіть якщо ці корені є ірраціональними або комплексними. Наприклад, розглянемо рівняння
Виділення квадрата дає
отже
Потім
Лаконічніше:
Отже,
Рівнянь з комплексними коренями можуть бути розв'язані таким же чином. Наприклад:
Загальний вигляд
Для незведених квадратних рівнянь першим кроком до їх розв'язання є розділити на коефіцієнт при х2. Наприклад:
Застосування
Інтегрування
Виділення квадрату може бути використане для обчислення інтегралів виду
з використанням основних інтегралів
Наприклад, розглянемо інтеграл
Виділення квадрата в знаменнику дає:
Це може бути обчислено з допомогою підстановки у = х + 3, яка дає
Комплексні числа
Розглянемо вираз
де z і b є комплексними числами, z* і b* є комплексно спряжені до z, та b, відповідно, а c — це дійсне число. Використовуючи властивість |у|2 = уу* , ми можемо переписати вираз як
що має дійсне значення. Це відбувається тому, що
Розглянемо інший приклад, вираз
де a, b, c, x і y — дійсні числа, причому а > 0 і b > 0, може бути виражена як квадрат абсолютного значення комплексного числа. Визначимо
Тоді
отже,
Ідемпотентна матриця
Матриця М є ідемпотентною, якщо М 2 = М. Ідемпотентні матриці узагальнюють ідемпотентні властивості 0 і 1. Виділення квадрату в рівнянні
показує, що деякими ідемпотентними 2 × 2 матрицями параметризують коло в (А, B)-площині.
Матриця буде ідемпотентом за умови що, при виділенні квадрату стає
В (А, B)-площині — це рівняння кола з центром у точці (1/2, 0) і радіусом 1/2.
Геометрична інтерпретація
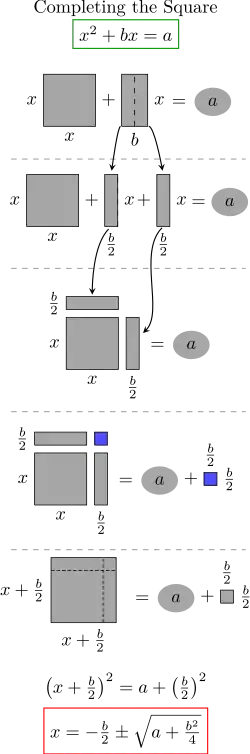
Розглянемо виділення квадрату для рівняння
Оскільки х2 являє собою площу квадрата зі стороною довжини х і bx являє собою площу прямокутника зі сторонами b і x, процес виділення квадрата можна розглядати як візуальні маніпуляції прямокутників.
Прості спроби об'єднати квадрат х2 і прямокутник bx у великий квадрат не дають результату. Доданок (b/2)2 потрібно додати до кожної сторони рівняння — це саме та ділянка, якої не вистачає до повного квадрату, звідки походить термін «виділити квадрат».
Використання у техніці
Зазвичай повний квадрат складається з трьох складових, додамо v 2 до
щоб отримати квадрат. Є також випадки, в яких можна додати середній член тричлена, або 2uv або −2uv, щоб
стало повним квадратом.
Приклад: сума числа і оберненого до нього числа
Написавши
ми бачимо, що сума числа х і оберненого до нього числа завжди більше або дорівнює 2. Квадрат виразу завжди більше або дорівнює нулю, коли х дорівнює 1.
Приклад: розкладання многочлена 4-го степеня
Розглянемо проблему розкладання на множники многочлена
Запишемо його у вигляді
тому середній член 2(х2)(18) = 36х2. Таким чином, ми отримуємо
Примітки
- Narasimhan, Revathi (2008). Precalculus: Building Concepts and Connections. Cengage Learning. с. 133–134. ISBN 0-618-41301-4.
Джерела
- Алгебра 1, Гленко, ISBN 0-07-825083-8, стор 539—544
- Алгебра 2, Саксон, ISBN 0-939798-62-X, стор 214—214, 241—242, 256—257, 398—401