Гіперпрямокутник

n-гіперпрямокутник [1] — це узагальнення прямокутника на вищі розмірності і формально визначається як прямий добуток проміжків.

Гіперпрямокутник
n-прямокутник

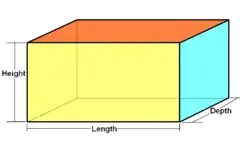Прямокутний паралелепіпед є 3-прямокутником
ТипПризма
Фасет2n
Вершин2n
Символ Шлефлі{} × {} … × {}
Діаграма Коксетера — Динкіна …
Група симетрії[2n-1], порядок 2n
Двоїстий
багатогранник		Прямокутний n-ромб
Властивостіопуклий, зоноедр, ізогональний

Типи

Тривимірний гіперпрямокутник називається також прямокутною призмою або прямокутним паралелепіпедом.

Особливий випадок n-прямокутника, в якому всі ребра мають однакову довжину, є n-кубом [1] .

За аналогією термін «гіперпрямокутник» застосовують до прямого добутку ортогональних інтервалів іншого виду, таких як діапазони ключів у базі даних або діапазони цілих чисел, а не дійсних чисел[2] .

Двоїстий багатогранник
n-ромб

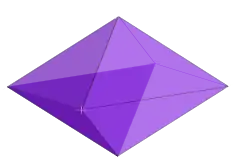Приклад: 3-ромб
Фасет2n
Вершин2n
Символ Шлефлі{} + {} + … + {}
Діаграма Коксетера — Динкіна …
Група симетрії[2n-1], порядок 2n
Двоїстий
багатогранник		n-прямоугольник
Свойстваопуклий, ізогональний

Двоїстий багатогранник n-прямокутника називають n-ортоплексом або n-ромбом. Багатогранник будується за 2n точками в центрах прямокутних фасет прямокутника.

Символ Шлефлі n-ромба подається сумою n ортогональних відрізків: {} + {} + … + {}.

1-ромб — це відрізок. 2-ромб — це ромб.

n Приклад
1
{}
2
{ } + { }
3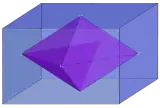
Ромбічний 3-ортоплекс всередині 3-прямокутника
{ } + { } + { }

Див. також

Примітки
  1. Coxeter, 1973, с. 122–123.
  2. W. Rectangular par

Література
  • Coxeter H. S. M.D. Regular Polytopes. — 3rd. — New York : Dover, 1973. — ISBN 0-486-61480-8.
  • Yi Zhang, Kamesh Munagala, Jun Yang. Storing matrices on disk: Theory and practice revisited // Proc. VLDB. — 2011. — Т. 4, вип. 11 (21 лютого). — С. 1075–1086.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.