Гіпотеза Тепліца

Гіпотеза Тепліца також відома як гіпотеза про вписанний квадрат — невирішена проблема геометрії. Формулювання гіпотези:

На усякій простій замкнутій плоскій жордановій кривій можна відшукати чотири точки, які будуть вершинами квадрату.
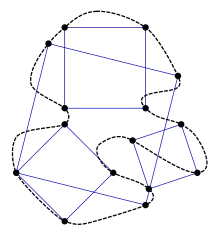
Пунктирна крива проходить через вершини кількох квадратів

Гіпотеза Тепліца вірна для опуклих або кусково-гладких кривих та в деяких інших спеціальних випадках. Проблема була сформульована Отто Тепліцем в 1911 році[1]. Ранні позитивні результати були отримані Арнольдом Емчем[2] і Левом Шнірельманом[3]. Станом на 2015 рік гіпотеза в загальному випадку залишається не вирішеною[4].

Формулювання проблеми

Многокутник P вписаний в криву Жордана C, якщо всі вершини P належать C. Проблема вписаного квадрата полягає в наступному:

Чи можна на кожній кривій Жордана відшукати вписаний квадрат?

При цьому обмежень на послідовність, в якій будуть вершини квадрата на кривій, не накладається.

Приклади

Для деяких кривих, наприклад, для кола та квадрата, можна вказати нескінченно багато вписаних квадратів. В тупокутний трикутник можна вписати рівно один квадрат; в прямокутний — рівно два, а в гострокутний — рівно три[5].

Вирішені випадки

Спокусливо спробувати розв'язати проблему вписаного квадрата, довівши, що спеціальний клас кривих завжди містить вписаний квадрат, а потім наблизитись до довільної кривої послідовністю таких кривих та зробити висновок, що для цієї кривої існує вписаний квадрат, як межа квадратів, вписаних в криві послідовності. Одна з проблем такого підходу полягає в тому, що межею послідовність квадратів може бути єдина точка, а не квадрат. Тим не менш, відомо багато класів кривих для яких існує вписаний квадрат[4].

Кусково-аналітичні криві

Емч (1916) показав, що кусково аналітичні криві завжди містить вписаний квадрат[2]. Зокрема, це вірно для багатокутників. Доведення Емча криві які проходять через середини січних відрізків кривої, які паралельні заданій лінії. Він показує, що, коли ці криві перетинаються з кривими, що породжені таким самим чином для ортогональної лінії, то буде непарне число перетинів. Таким чином, завжди існує принаймні один перетин, який є центром a ромбу вписаного в задану криву. При неперервному обертанні двох перпендикулярних ліній від нуля до прямого кута, і застосовуючи теорему про проміжне значення, Емч показує, що принаймні один з цих ромбів є квадрат[4].

Локально монотонні криві

Вальтер Стромквіст довів, що в кожну локально монотонну просту пласку криву можна вписати квадрат[6]. Доведення для локально монотонних кривих C наступне: для будь-якої точки p, що лежить на C, існує такий окіл U(p), що жодна хорда C в цьому околі не є паралельною заданому напрямку n(p) (напрямку осі ординат). До локально монотонних кривих належать всі опуклі криві і всі кусково-задані безперервно диференційовані криві без точок повернення.

Криві без спеціальних трапецій

Навіть за більш слабкої умови ніж локальна монотонність, для ε > 0, крива не має вписаних спеціальних трапецій розміру ε. Спеціальна трапеція — рівнобічна трапеція з трьома однаковими сторонами, кожна довше ніж четверта сторона, вписується в криву з порядком вершин відповідним до годинникового впорядкування самої кривої. Якщо немає таких трапецій (або навіть парної кількості їх), то для загальних кривих може бути доведено, що криві, які володіють цією властивістю завжди містять вписаний квадрат[4].

Криві в кільцях

Якщо жорданова крива вписана в кільце зовнішній радіус якого не більше ніж в разів внутрішнього радіусу, і розташована таким чином, що вона відокремлює внутрішнє коло кільця від зовнішнього кола, то крива містить вписаний квадрат. У цьому випадку, великі вписані квадрати, які містять центр кільця, топологічно відділені від менших вписаних квадратів, які не містять центр. Межа послідовності великих квадратів знову буде великим квадратом, можливо навіть виродиться в точку, тим самим метод збіжної послідовності може бути застосований в цьому випадку[4].

Симетричні криві

Позитивна відповідь також відома для центрально-симетричних кривих[7].

Варіанти та узагальнення

Відомо, що для будь-якого заданого трикутника T і жорданової кривої C існує трикутник, подібний T і вписаний в C[8][9]. Більш того, множина вершин таких трикутників є щільною в C[10]. Зокрема, завжди існує вписаний рівносторонній трикутник. Також в будь-яку жорданову криву можна вписати прямокутник.

У деяких узагальненнях проблеми вписаного квадрата розглядаються вписані в криві багатокутники. Існують також узагальнення для багатовимірних евклідових просторів. Так, Стромквіст довів, що в будь-яку неперервну замкнену криву , що задовольняє «умові A», можна вписати чотирикутник з рівними сторонами та рівними діагоналями; «Умова A» полягає в тому, що ніякі дві хорди C у відповідному околі будь-якої точки не повинні бути перпендикулярними[6]. Цей клас кривих включає всі криві C2. Нільсен і Райт довели, що будь-який симетричний континуум містить вписані прямокутники[7]. Генріх Гуггенхаймер довів, що будь-яка гіперповерхня, C3-дифеоморфна гіперсфері Sn−1, містить 2n вершин правильного евклідового гіперкубу[11].

Примітки
  1. Toeplitz, O.: Ueber einige aufgaben der analysis situs Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn, 94 (1911), p. 197.
  2. Emch, Arnold (1916). On some properties of the medians of closed continuous curves formed by analytic arcs. American Journal of Mathematics 38 (1): 6–18. MR 1506274. doi:10.2307/2370541.
  3. Лев Шнирельман. . — Т. 10.
  4. Matschke, Benjamin (2014). A survey on the square peg problem. Notices of the American Mathematical Society 61 (4): 346–253. doi:10.1090/noti1100..
  5. Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71 (4), 1998, 278–284.
  6. Stromquist, Walter (1989). Inscribed squares and square-like quadrilaterals in closed curves. Mathematika 36 (2): 187–197. MR 1045781. doi:10.1112/S0025579300013061.
  7. Нільсен, Mark J.; Wright, S. E. (1995). Rectangles inscribed in symmetric continua. Geometriae Dedicata 56 (3): 285–297. MR 1340790. doi:10.1007/BF01263570.
  8. Meyerson, Mark D. (1980). Equilateral triangles and continuous curves. Fundamenta Mathematicae 110 (1): 1–9. MR 600575..
  9. Kronheimer, E. H.; Kronheimer, P. B. (1981). The tripos problem. Journal of the London Mathematical Society. Second Series 24 (1): 182–192. MR 623685. doi:10.1112/jlms/s2-24.1.182.
  10. Нільсен, Mark J. (1992). Triangles inscribed in simple closed curves. Geometriae Dedicata 43 (3): 291–297. MR 1181760. doi:10.1007/BF00151519.
  11. Guggenheimer, H. (1965). Finite sets on curves and surfaces. Israel Journal of Mathematics 3: 104–112. MR 0188898. doi:10.1007/BF02760036.

Додаткова література
  • Victor Klee and Stan Wagon, Old and New Unsolved Problems in Plane Geometry and Number Theory, The Dolciani Mathematical Expositions, Number 11, Mathematical Association of America, 1991

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.