Мережа радіальних базисних функцій
Мережа радіально базисних функцій у математичному моделюванні — це штучна нейронна мережа, яка використовує радіальні базисні функції у якості функції активації. Виходом мережі є лінійна комбінація радіальних базисних функцій входу та параметрів нейрона. Мережі радіальних базисних функцій мають багато застосувань, зокрема, такі як апроксимацію функції, прогнозування часових рядів, задачі класифікації та керування системою. Вони були вперше сформульовані у статті 1988 року Брумхедом і Лоу, обидва дослідники з Royal Signals and Radar Establishment.[1][2][3]
Архітектура мережі
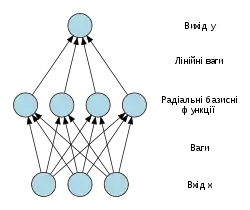
Мережі радіально базисних функцій (RBF) зазвичай мають три шари: вхідний шар, прихований шар з нелінійною RBF функцією активації та лінійний вихідний рівень. Вхід можна моделювати як вектор дійсних чисел . Вихід мережі тоді, є скалярною функцією вхідного вектора, , і має вигляд
де — кількість нейронів у прихованому шарі, є центральним вектором для нейрона , та — це вага нейрона в лінійному виході нейронів. Функції, які залежать лише від відстані від центру вектора, є радіально симетричними щодо цього вектора, отже, називаються радіальною базисною функцією. У базовій формі всі входи пов'язані з кожним прихованим нейроном. За норму, як правило, обирається Евклідова відстань (хоча відстань Махаланобіса, загалом, більш пасує), та радіальна базисна функція зазвичай вважається розподілом Ґауса
- .
Гаусові базисні функції близькі до центрального вектора в тому сенсі, що
тобто зміна параметрів одного нейрона має лише невеликий ефект для вхідних значень, що знаходяться далеко від центру цього нейрона.
Завдяки гнучким умовам на форму функції активації, RBF мережі є універсальними апроксиматорами на компактному просторі . Це означає, що мережа RBF з достатньою кількістю прихованих нейронів може апроксимувати будь-яку неперервну функцію на замкненій обмеженій множині з довільною точністю.
Параметри , , та визначаються так, щоб оптимізують відповідність між і даними.
Нормалізація
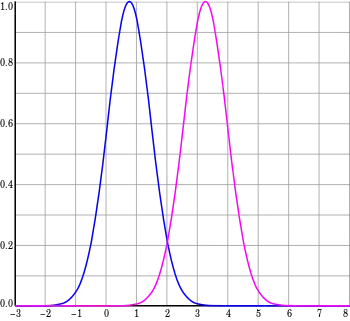
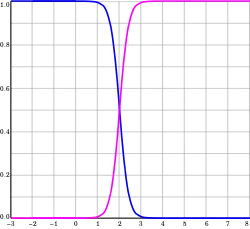
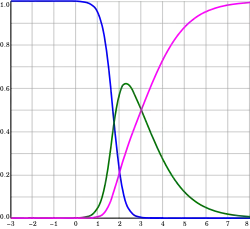
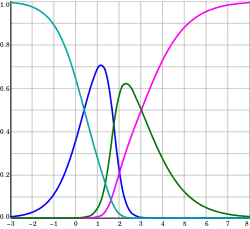
Нормалізована архітектура
Окрім вищезгаданої ненормалізованої архітектури, мережі RBF можуть бути нормалізовані. У цьому випадку є відображення
де
відома як «нормована радіально-базисна функція».
Теоретична мотивація для нормалізації
Існує теоретичне обґрунтування цієї архітектури у випадку стохастичного потоку даних. Припустимо, що апроксимація стохастичного ядра для спільної щільності ймовірностей
де ваги та є зразками даних, і нам потрібно, щоб ядра нормалізувались
і
- .
Щільність ймовірностей у вхідному та вихідному просторах є
і
Очікування у введеного на вхід
де
умовна ймовірність y при заданому . Умовна ймовірність пов'язана з ймовірністю теоремою Баєса.
який дає
- .
Це стає
коли виконується інтегрування.
Локальні лінійні моделі
Іноді зручно розширювати архітектуру, щоб включити локальні лінійні моделі. У цьому випадку архітектури зводяться до першого порядку,
і
в ненормалізованих та нормалізованих випадках, відповідно. Тут визначаються ваги . Можливі також вирази більш високого порядку від лінійних термів. Цей результат можна записати як
де
і
в ненормалізованому випадку і
в нормалізованому. Тут є дельто-функцією Кронекера і визначається як
- .
Навчання
Мережі RBF, як правило, тренуються з пар вхідних і цільових значень , , за двохетапним алгоритмом. На першому етапі обирається центр вектору RBF функції у прихованому шарі. Цей етап виконується кількома способами; центри можуть бути випадково відібрані з деякого набору прикладів, або їх можна визначити за допомогою кластеризації методом к–середніх. Зауважте, що цей крок не контролюється. Другий крок просто відповідає лінійній моделі з коефіцієнтами до виходів прихованого шару з відношенням до деякої цільової функції. Загальна цільова функція, принаймні для регресії/оцінки функції, є функцією найменших квадратів:
де
- .
Ми маємо явне включення залежності від ваг. Мінімізація цільової функції найменших квадратів за оптимального вибору ваг оптимізує точність підгонки.
Є випадки, коли потрібно оптимізувати багато цілей, таких як гладкість, а також точність. У цьому випадку корисно оптимізувати регуляризовану цільову функцію, таку як
де
і
де оптимізація S максимізує гладкість та відома, як регуляризація.
Третій, не обов'язковий етап зворотного поширення помилки, може бути виконаний для точного настроювання всіх параметрів мережі RBF.[3]
Інтерполяція
RBF мережі можуть бути використані для інтерполяції функції коли значення цих функцій відомі на кінцевому числі точок: . Взяття відомих точок щоб бути центрами радіальних базисних функцій і оцінювати значення основних функцій в тих самих точках ваги можуть бути знайдені з рівняння
Може бути доведено, що інтерполяція матриці у вищенаведеному рівнянні є несингулярною, якщо точки відрізняються, а отже ваги можуть бути знайдені за допомогою простої лінійної алгебри:
Апроксимація функції
Якщо мета полягає не в тому, щоб виконувати жорстку інтерполяцію, а натомість більш загальну апроксимацію функції або класифікацію, оптимізація дещо складніша, оскільки для центрів немає очевидного вибору. Тренування, як правило, виконуються в два етапи, спочатку фіксуючи ширину та центри, а потім ваги. Це можна виправдати, розглядаючи різну природу нелінійних прихованих нейронів у порівнянні з лінійним вихідним нейроном.
Підготовка центрів базисних функцій
Центри базисних функцій можуть бути випадково відібрані серед вхідних екземплярів або отримані в рамках ортогонального алгоритму навчання найменшої квадрату або знайдені за допомогою кластерізації зразків та вибору кластеризації як центрів.
Ширина RBF, як правило, закріплена за тим самим значенням, яке пропорційно максимальній відстані між вибраними центрами.
Псевдообернене рішення для лінійної ваги
Після того, як центри зафіксовані, ваги, що мінімізують похибку на виході, обчислюються за допомогою лінійного псевдооберненого рішення:
- ,
де записи G є значеннями радіальних базисних функцій, оцінених в точках : .
Існування цього лінійного рішення означає, що на відміну від багатошарових персептронних (MLP) мереж, RBF мережі мають унікальний локальний мінімум (коли центри фіксуються).
Метод градієнтного спуску навчання лінійних ваг
Інший можливий алгоритм тренування — градієнтний спуск.Під час тренування градієнтного спуску ваги коригуються на кожному кроці, рухаючи їх у напрямку, протилежному градієнту об'єктивної функції (таким чином, можна знайти мінімум об'єктивної функції),
де це «навчальний параметр».
Для випадку тренування лінійних ваг, , алгоритм стає
в ненормалізованому випадку і
в нормалізованому.
Для локальної лінійної архітектури навчання градієнт-спуском є
Тренування оператора проектування лінійних ваг
Для випадку тренування лінійних ваг, та , алгоритм стає
в ненормалізованому випадку і
в нормалізованому і
в локально-лінійному випадку.
Для однієї базової функції тренування оператора проекції зводиться до метода Ньютона.
Приклади
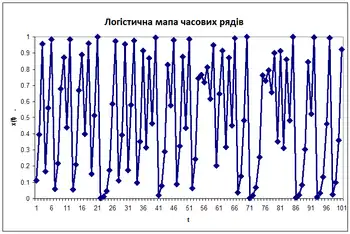
Логістична карта
Основні властивості радіально-базисних функцій можна проілюструвати простим математичним відображенням, логістичне відображення, яке відображає інтервал одиниці на себе. Він може бути використаний для створення зручного прототипу потоку даних. Логістичне відображення може бути використане для вивчення апроксимації функції, прогнозування часових рядів і теорії керування. Відображення походить з поля популяційна динаміка і стало прототипом для хаосу часових рядів. Відображення в повністю хаотичному режимі дається
- ,
де t — індикатор часу. Значення х у момент t+1 є параболічною параболічною функцією х від часу t. Це рівняння представляє основну геометрію хаосу часових рядів, що породжуються логістичною картою.
Покоління часових рядів з цього рівняння є оберненою задачею; ідентифікація основної динаміки або фундаментального рівняння логістичної карти з примірників часових рядів. Мета — знайти оцінку
для f.
Апроксимація функції
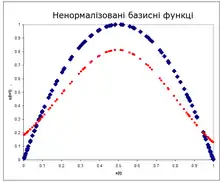
Ненормовані радіально базисні функції
Архітектурою є
де
- .
Примітки
- Broomhead, D. S.; Lowe, David (1988). Radial basis functions, multi-variable functional interpolation and adaptive networks (4148).
- Broomhead, D. S.; Lowe, David (1988). Multivariable functional interpolation and adaptive networks. Complex Systems 2: 321–355.
- Schwenker, Friedhelm; Kestler, Hans A.; Palm, Günther (2001). Three learning phases for radial-basis-function networks. Neural Networks 14: 439–458. doi:10.1016/s0893-6080(01)00027-2.