Розділення секрету

Через дві точки можна провести необмежену кількість поліномів ступеня 2. Щоб вибрати з них єдиний — потрібна третя точка

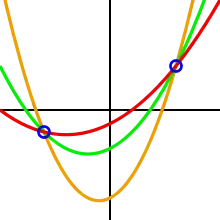
Ідея схеми полягає в тому, що двох точок достатньо для задання прямої, трьох крапок — для завдання параболи, чотирьох точок — для кубічної параболи, і так далі. Щоб задати многочлен ступеня ${\displaystyle k}$ потрібно ${\displaystyle k+1}$ точок.

Для того, щоб після поділу секрет могли відновити тільки ${\displaystyle k}$ учасників, його «ховають» у формулу многочлена ступеня ${\displaystyle (k-1)}$ над кінцевим полем ${\displaystyle G}$. Для однозначного відновлення цього многочлена необхідно знати його значення ${\displaystyle k}$ точках, причому, використовуючи меншу кількість точок, однозначно відновити початковий многочлен не вийде. Кількість різних точок многочлена не обмежена (на практиці воно обмежується розміром числового поля ${\displaystyle G}$, в якому ведуться розрахунки).

Коротко даний алгоритм можна описати наступним чином. Нехай дано кінцеве поле ${\displaystyle G}$. Зафіксуємо ${\displaystyle n}$ різних ненульових несекретних елементів даного поля. Кожен з цих елементів приписується певному члену групи. Далі вибирається довільний набір з ${\displaystyle t}$ елементів поля ${\displaystyle G}$, з яких складається многочлен ${\displaystyle f(x)}$ над полем ${\displaystyle G}$ ступеня ${\displaystyle t-1,1<t\leq n}$. Після отримання многочлена вираховуємо його значення в несекретних точках і повідомляємо отримані результати відповідним членам групи[1].

Щоб відновити секрет можна скористатися інтерполяційної формули, наприклад формулою Лагранжа.

Важливою перевагою схеми Шаміра є те, що вона легко масштабована[6]. Щоб збільшити число користувачів в групі, необхідно лише додати відповідне число несекретних елементів до вже існуючих, при цьому має виконуватися умова ${\displaystyle r_{i}\neq r_{j}}$ при ${\displaystyle i\neq j}$. У той же час, компрометація однієї частини секрету переводить схему з ${\displaystyle (n,t)}$ -порогової в ${\displaystyle (n-1,t-1)}$-порогову.

Дві непаралельні прямі на площині перетинаються в одній точці. Будь-які дві некомпланарні площини перетинаються по одній прямій, а три некомпланарні площини в просторі теж перетинаються в одній точці. Взагалі n n-мірних гіперплощин завжди перетинаються в одній точці. Одна з координат цієї точки буде секретом. Якщо закодувати секрет як декілька координат точки, то вже по одній частці секрету (однієї гіперплощини) можна буде отримати якусь інформацію про секреті, тобто про взаємозалежності координат точки перетину.

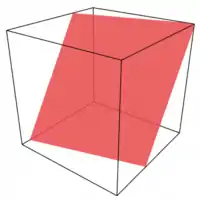
Схема Блеклі у трьох вимірах: кожна частка секрету — це площина, а секрет — це одна з координат точки перетину площин. Двох площин недостатньо для визначення точки перетину.

З допомогою схеми Блеклі[5] можна створити (t, n)-схему розподілу секрету для будь-яких t і n: для цього треба покласти розмірність простору дорівнює t, і кожному з n гравців дати одну гіперплощина, що проходить через секретну точку. Тоді будь — t з n гіперплощин будуть однозначно перетинатися в секретній точці.

Схема Блеклі менш ефективна, ніж схема Шаміра: у схемі Шаміра кожна частка такого ж розміру, як і секрет, а в схемі Блеклі кожна частка в t разів більше. Існують поліпшення схеми Блеклі, що дозволяють підвищити її ефективність.

У 1983 році Моріс Миньотт, Асмут і Блум запропонували дві схеми поділу секрету, засновані на китайській теоремі про залишки. Для деякого числа (у схемі Міньотта це сам секрет, у схемі Асмута — Блума — деяке похідне число) обчислюються залишки від ділення на послідовність чисел, які роздаються сторонам. Завдяки обмеженням на послідовність чисел, відновити секрет може тільки певне число сторін[8][9].

Нехай кількість користувачів в групі дорівнює ${\displaystyle n}$. У схемі Міньотта вибирається деяка множина попарно взаємно простих чисел ${\displaystyle \{m_{1},m_{2},...,m_{n}\}}$ таких, що добуток ${\displaystyle k-1}$менше, ніж добуток ${\displaystyle k}$ найменших з цих чтсел. Нехай ці добутки рівні ${\displaystyle M}$${\displaystyle N}$, відповідно. Число ${\displaystyle k}$ називається порогом для схеми, що конструюється по множині${\displaystyle \{m_{1},m_{2},...,m_{n}\}}$. В якості секрету обирається число ${\displaystyle S}$ таке, для якого виконується співвідношення ${\displaystyle M<S<N}$. Частини секрету розподіляються між учасниками групи наступним чином: кожному учаснику видається пара чисел ${\displaystyle (r_{i},m_{i})}$, де ${\displaystyle r_{i}\equiv S{\pmod {m_{i}}}}$.

Щоб відновити секрет, необхідно об'єднати ${\displaystyle t\geq k}$ фрагментів. В цьому випадку отримаємо систему порівнянь виду ${\displaystyle x\equiv r_{i}{\pmod {m_{i}}}}$, множину рішень якої можна знайти, використовуючи китайську теорему про залишки. Секретне число ${\displaystyle S}$${\displaystyle S<m_{1}\cdot m_{2}\cdot ...\cdot m_{t}}$. Також не складно показати, що якщо число фрагментів менше ${\displaystyle k}$, то, для того щоб знайти секрет ${\displaystyle S}$, необхідно перебрати близько ${\displaystyle {\frac {N}{M}}}$ цілих чисел. При правильному виборі чисел ${\displaystyle m_{i}}$ такий перебір практично неможливо реалізувати. Наприклад, якщо розрядність ${\displaystyle m_{i}}$ буде від 129 до 130 біт, а ${\displaystyle k<15}$, то відношення ${\displaystyle {\frac {N}{M}}}$ буде мати порядок ${\displaystyle 2^{100}}$[10].

Схема Асмута — Блума є доопрацьованою схемою Міньотта. На відміну від схеми Міньотта, її можна побудувати в такому вигляді, щоб вона була досконалою[11].

У 1983 році Карнін, Грін і Хеллман запропонували свою схему розподілу секрету, яка ґрунтувалася на неможливості вирішити систему з ${\displaystyle m}$ невідомими, маючи менше ${\displaystyle m}$ рівнянь[12].

У рамках даної схеми вибираються ${\displaystyle n+1}$ ${\displaystyle m}$-мірних векторів ${\displaystyle V_{0},V_{1},...,V_{n}}$ так, щоб будь-яка матриця розміром ${\displaystyle m\times m}$, складена з цих векторів, мала ранг${\displaystyle m}$. Нехай вектор ${\displaystyle U}$ має розмірність ${\displaystyle m}$.

Секретом в схемі є матричний добуток ${\displaystyle U^{T}\cdot V_{0}}$. Частками секрету є добуток ${\displaystyle U^{T}\cdot V_{i},1\leq i\leq n}$.

Маючи будь-які ${\displaystyle m}$ часток, можна скласти систему лінійних рівнянь розмірності ${\displaystyle m\times m}$, невідомими якої є коефіцієнти ${\displaystyle U}$. Розв'язавши дану систему, можна знайти ${\displaystyle U}$, а маючи ${\displaystyle U}$ можна знайти секрет. При цьому система рівнянь не має рішення в разі, якщо часток менше, ніж ${\displaystyle m}$[13].

Існуює кілька способів порушити протокол роботи порогової схеми:

• власник однієї з часток може перешкодити відновленню загального секрету, віддавши в потрібний момент невірну (випадкову) частку[14];
• зловмисник, не маючи частки, може бути присутнім при відновленні секрету. Дочекавшись оголошення потрібного числа часток, він швидко відновлює секрет самостійно і породжує ще одну частку, після чого пред'являє її іншим учасникам. В результаті він отримує доступ до секрету і залишається не пійманим[15].

Також існують інші можливості порушення роботи, не пов'язані з особливостями реалізації схеми:

• зловмисник може зімітувати ситуацію, при якій необхідно розкриття секрету, тим самим вивідавши частки учасників[15].