Розподіл Лапласа
В теорії імовірності і статистиці Розподіл Лапласа належить до сім'ї неперервних розподілів. Названо на честь французького математика П'єра-Симона Лапласа. Інколи вживають назву подвійний експоненційний розподіл, маючи на увазі, що графік щільності розподілу Лапласа виглядає як симетрично продовжена (на від'ємній півосі) щільність експоненційного розподілу.
| Розподіл Лапласа | |
|---|---|
 | |
|
Функція розподілу ймовірностей 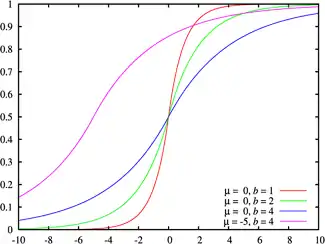 | |
| Параметри |
параметр локалізації (дійсний) параметр масштабу (дійсний) |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | Дивіться текст |
| Середнє | |
| Медіана | |
| Мода | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Ентропія | |
| Твірна функція моментів (mgf) | для |
| Характеристична функція | |
Різниця значень двох незалежних однаково розподілених експоненційних випадкових величин розподілена за розподілом Лапласа, також Броунівський рух в експоненційно розподіленій точці часу розподілений за Лапласом.
Характеристики
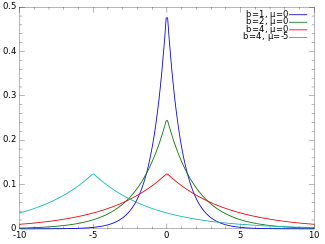
Щільність розподілу
Випадкова величина розподілена з розподілом Лапласа, X~Lap(μ,b), має щільність:
де, μ — параметр локалізації і b > 0 параметр масштабу. Якщо μ = 0 і b = 1, додатня частина розподілу є точно половина експоненційного розподілу.
Щільність розподілу Лапласа нагадує щільність нормального розподілу, з тією відмінністю, що вираз щільності нормального розподілу містить квадрат різниці значення і математичного сподівання (μ), а у виразі для щільності Лапласового розподілу модуль цієї різниці. Як наслідок Лапласів розподіл має товстіші хвости в порівнянні з нормальним розподілом.
Функція розподілу
Функцію розподілу легко отримати проінтегрувавши щільність і використовуючи симетричність щільності відносно параметра μ. Функція розподілу має вигляд:
Обернене до функції розполу записується:
Математичне сподівання і дисперсія
В показнику експоненти щільності маємо модуль різниці, тому інтервал необхідно розбити на і (функція щільності симетрична відносно цих інтервалів). Інтеграли беруться частинами, при підстановці нескінченостей () розглядаємо границі вигляду .
Моменти
Застосовуючи формулу інтегрування частинами декілька раз, отримуємо:
Після підстановок границь інтегрування:
Оскільки перший інтеграл залежить від парності k розглядаються двавипадки: k — парне і k — непарне:
Або, в загальному вигляді:
, де — ціла частина x.
Генерація випадкових величин розподілених за Лапласом
Нехай маємо випадкову величину U рівномірно розподілену на інтервалі (-1/2, 1/2], тоді випадкова величина
розподілена за розподілом Лапласа з параметрами μ and b. Це видно якщо розглянути функцію обернену до функції розподілу, яка наведена вище.
Випадкову величину ~ можна також згенерувати як різницю двох н.о.р. випадкових величин. Або ще випадкову величину ~ можна згенерувати як логарифм частки двох н.о.р. рівномірно розподілених випадкових величин.