Світ тісний (граф)
Граф «Світ тісний» (маленький світ) — різновид графа, який має таку властивість: якщо взяти дві довільні вершини a і b, то вони з великою ймовірністю не є суміжними, проте одна досяжна з іншої за допомогою невеликої кількості переходів через інші вершини. А саме, граф «Світ тісний» визначається як мережа, в якій типова відстань L між двома довільно обраними вершинами (кількість кроків, необхідних, щоб досягти одну з іншої) зростає пропорційно логарифму від числа вершин N в мережі, таким чином[1]:
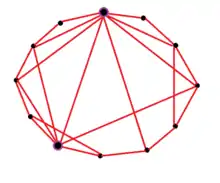
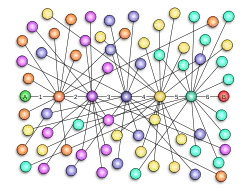
У контексті соціальної мережі це призводить до феномену «Світ тісний», тобто незнайомих людей пов'язує невелика кількість проміжних знайомих. Багато реально існуючих графів добре моделюються через графи «Світ тісний». Соціальна мережа, зв'язаність мережі Інтернет, вікі-сайти, такі, як Вікіпедія, і генні мережі виявляють властивості графа «Світ тісний». Дункан Воттс і Стівен Строгац в 1998 році ідентифікували певну категорію графів «Світ тісний» як клас випадкових графів. Вони відзначили, що такі графи можуть бути класифіковані відповідно з двома незалежними структурними особливостями, а саме коефіцієнт кластеризації та відстань від однієї вершини до іншої в середньому (також відоме як довжина найкоротшого шляху в середньому). Цілком випадкові графи, побудовані відповідно з моделлю Ердеша — Реньї, мають малу довжину найкоротшого шляху в середньому (вона росте як логарифм від кількості вершин у графі) і маленький коефіцієнт кластеризації. Воттс і Строгац з'ясували, що більшість реально існуючих мереж мають малу довжину найкоротшого шляху в середньому, але коефіцієнт кластеризації в них істотно вище, ніж очікується при випадковому виборі. Після цього Ватц і Строгац запропонували нову модель графа, в даний час звану Модель Воттса — Строгаца, для якої характерні (i) мала довжина найкоротшого шляху в середньому, і (ii) великий коефіцієнт кластеризації. Перетин в моделі Воттса і Строгаца між «великим світом» (таким, як ґратчастий граф) і маленьким світом було вперше описане Бартелмі і Амарал в 1999[2]. Після цієї роботи сталась велика кількість досліджень[3][4][5].
Властивості графа «Світ тісний»
Графи «Світ тісний» мають тенденцію містити в собі кліки і майже-кліки, під якими розуміють підмережі, які мають зв'язки майже між усіма вершинами в них. Це випливає з визначення такої властивості графа, як високий коефіцієнт кластеризації. По-друге, більшість пар вершин будуть з'єднані хоча б одним коротким шляхом. Більш строго: відстань від однієї вершини до іншої в середньому (також відоме як довжина найкоротшого шляху в середньому) відносно мало. Довжина найкоротшого шляху в середньому вираховується за такою формулою[6]:
- — відстань від вершини до вершини
- — кількість вершин у графі
Деякі інші особливості, які будуть описані далі, часто присутні в графах «Світ тісний». Зазвичай в таких графах є достаток хабів — вершин, у яких велика ступінь вершини. Ці хаби грають роль загального з'єднання, є сполучною ланкою в найкоротшому шляху між іншими ребрами. За аналогією, граф «Світ тісний» авіарейсів має малу довжину найкоротшого шляху в середньому (тобто між будь-якими двома містами у світі буде потрібно, ймовірно, не більше трьох перельотів) через те, що більшість авіарейсів проходять через вузлові аеропорти.
Для аналізу цієї властивості (а саме, наявності хабів) враховують частку вершин в мережі, які мають специфічне кількість вхідних з'єднань (ступінь розподілу мережі). Мережі з великою кількістю хабів, ніж очікується, будуть мати велику частку вершин з високим ступенем, отже, ступінь розподілу буде збільшуватися до високих значень. У розмовній мові це називається «розподіл важкого хвоста». Наявність у мережі високого ступеня розподілу, відповідної критерієм узгодженості з степеневим законом розподілу, є ознакою того, що мережа є графом «Світ тісний». Мережі зі степеневим законом розподілу також відомі як «безмасштабні мережі». Графи дуже різною топології класифікуються як графи «Світ тісний» до тих пір, поки виконуються зазначені вище дві умови (висока ступінь розподілу та відповідність степеневому закону).
Належність до класу графів «Світ тісний» оцінюється порівнянням кластеризації та довжини шляхів даної мережі з відповідними параметрами еквівалентної випадкової мережі з такою ж мірою розподілу[7]. Інший метод оцінювання приналежності мережі до класу графів «Світ тісний» використовує початкове визначення графа «Світ тісний», порівнюючи ступінь кластеризації даної мережі зі ступенем кластеризації еквівалентного графа-решітки і довжину середнього шляху з довжиною середнього шляху в довільному графі[8]. Міра приналежності графа до класу «Світ тісний» () визначається, як
- — довжина найкоротшого шляху в середньому в розглянутому графі
- — ступінь кластеризації розглянутого графа
- — довжина найкоротшого шляху в середньому у випадковому графі
- — ступінь кластеризації графа-решітки
Р. Коуен і Шломо Хавлін [9][10] показали аналітично, що безмасштабні мережі — ультра-малі світи. У цьому випадку, завдяки хабам, найкоротші шляхи стають істотно коротше і масштабуються, як
Приклади графів «Світ тісний»
Властивості графа «світ тісний» були виявлені в багатьох об'єктах реального світу, включаючи карти доріг, харчові ланцюжки, електричні мережі, мережі протікання метаболізму (metabolite processing networks), нейронні мережі, мережі виборців, граф телефонних дзвінків та мережі соціального впливу. Білок-білкові взаємодії мають таку властивість графа «Світ тісний», як відповідність степеневому закону розподілу[11]. Аналогічно, властивостями графа «Світ тісний» володіє регуляція транскрипції, в якій вершинам відповідають гени, причому вони пов'язані, якщо один ген має вгору або вниз регулювальний генетичний вплив на інший[12].
Приклади мереж, які не є графами «Світ тісний»
Малоймовірно, що мережі мають властивості графа «Світ тісний», якщо зв'язки між вершинами виникають головним чином через просторової або тимчасової близькості, тому що в такому випадку може не бути короткого шляху між двома «далекими» вершинами. Скрутність фізичним простором або часом, як у системі метро або в дорожніх мережах, як правило, перешкоджає формуванню особливо довгих зв'язків, які сприяють формуванню хабів.
У теорії шести рукостискань розглядаються люди, що живуть в один час. Якщо розглядати всіх людей, коли-небудь жили на Землі, то теорія шести рукостискань перестане працювати. Наприклад, кількість ступенів поділу між Альбертом Ейнштейном і Олександром Македонським більше 30, і ця мережа не має властивостей графа «Світ тісний». Аналогічні властивості є у мережі «піти до школи з»: якщо одна людина навчається в певному коледжі через 10 років після іншого, то малоймовірно, що вони познайомилися в цьому коледжі.
Точно так само, кількість станцій, через які повідомлення повинно пройти, не завжди було маленьким. У ті дні, коли пошта доставлялася з рук в руки або кінної поштою, кількість разів, яке лист передається з рук в руки між відправником та одержувачем було набагато більше, ніж сьогодні. Кількість разів, яке повідомлення передається з рук в руки між відправником та одержувачем в роки візуального телеграфу (близько 1800—1850) було визначено вимогою, що дві станції з'єднані лінією візуального контакту.
Неявні припущення, якщо не перевірені, можуть стати причиною необ'єктивності в літературі про графах на користь помилкової ідентифікації графів «Світ тісний» (наприклад картотека, що виникла через необ'єктивності публікації).
Надійність мережі
Деякими дослідниками (наприклад, Barabási) було висловлено припущення, що поширеність графів «Світ тісний» в біологічних системах може відображати еволюційна перевага такої топології. Приводом до такого припущення стала гіпотеза, що графи «Світ тісний» стійкіші при різних зовнішніх впливах в порівнянні з іншими топологіями мережі. Якби ця гіпотеза була вірна, то це забезпечило б перевагу біологічним системам, які є суб'єктами мутацій і вірусних інфекцій[13].
У графах «Світ тісний» зі степеневим законом розподілу ступенів вершин видалення випадкової вершини рідко служить причиною істотного збільшення найкоротшого шляху в середньому (або істотного зменшення коефіцієнта кластеризації). Це випливає з того факту, що більшість найкоротших шляхів проходять через хаби, і якщо периферична вершина видаляється, малоймовірно, що вона втрутиться в проходження між іншими периферійними вершинами. Оскільки частка периферійних вершин у графі «Світ тісний» істотно вище, ніж частка хабів, ймовірність видалення важливої вершини вкрай мала[14]. Наприклад, якщо маленький аеропорт в Петрозаводську перестане працювати, то це не збільшить середню кількість польотів, які потрібні пасажирам, щоб дістатися до точки призначення. Проте, якщо випадкове видалення потрапляє в хаб, довжина найкоротшого шляху в середньому може вирости досить істотно. Це можна побачити щорічно, коли північний аеропорт в США, такий, як Чиказький аеропорт О'Хара заносить снігом, і багато людей змушені летіти з пересадками і добиратися до пункту призначення обхідними шляхами.
На відміну від графа «Світ тісний», у випадковій мережі, в якій всі вершини мають приблизно однакову кількість з'єднань, видалення випадкової вершини збільшує довжину найкоротшого шляху в середньому незначно, але однаково для будь-якої віддаленої вершини. У цьому сенсі випадкові мережі уразливі до випадкових збурень в той час як графи «Світ тісний» стійкі[15]. Однак графи «Світ тісний» уразливі до спрямованих атак на хаби в той час як у випадкових мережах не можна вибрати цілі, знищення яких призведе до катастрофічних наслідків[16][17].
Відповідно, віруси еволюціонували таким чином, щоб взаємодіяти з протеїнами — хабами, такими як p53, тим самим вносячи суттєві зміни в поведінку клітин, сприятливі для відтворення вірусів[18].
Конструювання графів «Світ тісний»
Основний механізм конструювання графів «Світ тісний» — Модель Ватца — Строгаца.
Побудова графів «Світ тісний» з тимчасовим запізненням[19], дозволяє створювати не тільки фрактали, а й хаос при правильних умовах[20] або перехід до хаосу в динамічних мережах[21]. При розв'язанні задачі про ступінь діаметра конструюється граф, в якому кількість сусідів кожної вершини обмежена, в той час як відстань між будь-якою парою вершин (діаметр мережі) мінімізується. Конструювання таких графів «Світ тісний» здійснюється в рамках зусиль знаходження графів порядку, близького до межі Мура.
Інший шлях конструювання графів «Світ тісний» з нуля показаний у Бармпутіса і Мюррея[22], де будується мережа з дуже маленьким середньою відстанню і дуже великий середньої кластеризацією. Швидкий алгоритм константної складності даний разом з вимірами надійності отриманих графів. Залежно від галузі, можна почати з одного такого «ultra small — world» графа, і потім заново включити деякі ребра, або використовувати деякі маленькі такі мережі як підграф більшого графа.
Див. також: агрегація обмежена дифузією, утворення шаблонів
Застосування і додатки
Граф «Світ тісний» використовують для моделювання в різних галузях.
Додатки в соціології
Одна з переваг графів «Світ тісний» для громадського руху полягає в їх захищеності від фільтрувальних апаратів, що використовують сильно пов'язані вершини. Інша перевага — краща ефективність у передачі інформації при збереженні кількості посилань, необхідних для підключення до мережі на мінімальному рівні[23].
Модель графа «Світ тісний» безпосередньо застосовна до теорії споріднених груп, представленої в соціологічних аргументах Вільямом Фіннеганом. Спорідненні групи — це суспільні рухи, які є маленькими і напівзалежними, але ставлять перед собою значні мети і завдання. Незважаючи на те, що окремі учасники відносно незалежні і самостійні, декілька учасників, що володіють високим ступенем зв'язності, відповідають хабам в графі «Світ тісний» — є вершинами, що зв'язують різні групи. Така модель графа «Світ тісний» довела надзвичайно ефективну тактику організації протесту проти дій поліції[24]. Клей Ширки стверджує, що чим більше соціальна мережа ґрунтується на малих мережах, утворюючи граф «Світ тісний», тим більше цінні вершини високого ступеня зв'язності в цій мережі[23]. Те ж саме може бути сказано і про модель споріднених груп, де кілька людей в кожній групі з'єднані з зовнішніми групами, яким дозволена значно більша ступінь мобілізації та адаптації. Практичний приклад цього — граф «Світ тісний» через споріднені групи, які Вільям Фіннеган намітив в загальних рисах в протестах 1999 року в Сіетлі.
Додаток до наук про Землю
Багато мереж, що вивчаються в геології і геофізиці, за характеристиками схожі на граф «Світ тісний». Мережі, визначені в системі тріщин і пористих субстанцій, демонструють ці характеристики[25]. Сейсмічні мережі регіону Південної Каліфорнії можуть бути графами «Світ тісний»[26]. Наведені вище приклади зустрічаються на самих різних просторових масштабах, демонструючи масштабну інваріантність феномена в науках про Землю.
Додатки до обчислень
Графи «Світ тісний» були використані для оцінки можливості використання інформації, що зберігається у великих базах даних. Міра оцінки називається «Small World Data Transformation Measure»[27][28]. Чим більше зв'язки бази даних схожі на граф «Світ тісний» — тим більш імовірно що користувач буде в змозі витягти інформацію в майбутньому. Ця зручність зазвичай досягається за рахунок кількості інформації, що може зберігатися в тому ж сховищі.
P2P-мережа Freenet утворює граф «Світ тісний»[29], надаючи можливість зберігання і знаходження інформації таким чином, щоб ефективно масштабуватися при зростанні мережі.
Графи «Світ тісний» в нейронних мережах головного мозку
Анатомічні з'єднання в мозку[30] та мережі синхронізації коркових нейронів[31] представляють собою приклади графів «Світ тісний».
Граф «Світ тісний» з нейронів може проявляти властивості робочої пам'яті. Комп'ютерна модель, розроблена Соллі та ін.[32][33], має два стабільних стани; це властивість називається бістабільністю і вважається важливим у зберіганні пам'яті. Активуючий імпульс генерується самопідтримується петлями комунікаційної активності серед нейронів. Другий імпульс закінчує цю активність. Пульси перемикають систему між стабільними станами: потік (запис «пам'яті») і стан спокою (зберігання пам'яті).
На більш загальному рівні багато великих нейронні мережі головного мозку, такі як зорова система і стовбур головного мозку, виявляють властивості графа «Світ тісний»[34].
Граф «Світ тісний» в обчислювальній лінгвістиці і в завданнях з обробки тексту
Про історію та розвиток мов відомо мало. При тому, що мова — одне з найбільших досягнень людської еволюції! У всіх мов є спільні ознаки: наприклад, синтаксичні та семантичні категорії. Для більшості мов характерний закон Ципфа. Для вивчення різних властивостей мов використовуються мережі слів (тобто мережі, в яких вершинам відповідають слова, а ребрам — будь-які зв'язки між словами). Також вони можуть бути використані для обґрунтування різних гіпотез про розвиток мов. Наприклад, виходячи з подібності мов робиться висновок про наявність у них спільного предка. Однак подібність може бути викликане впливом мов один на одного і запозиченням слів[35].
У семантичній мережі англійської мови WordNet полісемія має величезний вплив на організацію семантичного графа. Через неї семантичний граф є графом «Світ тісний»[36]. Вершинами з високим ступенем (хабами), є вершини, що представляють абстрактні поняття, такі як лінія, голова, або коло[37].
Одне із завдань обробки природної мови — завдання ідентифікації авторства тексту. Один з методів — знаходження авторського інваріанта. Спочатку текст обробляється з нього віддаляються шумові слова (прийменники, сполучники тощо). Потім будується мережа, в якій вершини відповідають словам, а ребра проводяться між вершинами, які відповідають словам, які в тексті розташовані поруч. Встановлено, що отриманий граф є графом «Світ тісний»[38]. Якщо порахувати у мережі, побудованої за літературним твором, деякі параметри (наприклад, середню ступінь вершини, коефіцієнт кластеризації, кореляцію ступеня вершин), то можна помітити, що в творах одного автора ці параметри змінюються у відносно невеликому діапазоні, в той час як у різних авторів ці параметри відрізняються набагато сильніше[39].
Якщо представити статті Вікіпедії як вершини, а посилання між сторінками уявити ребрами між відповідними вершинами, то виходить граф, що володіє властивостями графа «Світ тісний». Причинами цього є вже згадувана належність до класу графів «Світ тісний» семантичної мережі слів, а так само наявність у Вікіпедії списків і категорій, що виконують роль хабів. Високий ступінь зв'язності Вікіпедії додатково підтримується проєктом «Зв'язність»[40]. На цій властивості Вікіпедії заснована гра, мета якої — за 5 кроків дістатися від випадкової статті до заданої.
Граф «Світ тісний» з розподілом довжини посилань
Модель графа «Світ тісний» включає рівномірний розподіл довжин посилань, що підкоряється степеневому закону розподілу, середня відстань між двома вершинами змінюється залежно від сили розподілу[41].
Децентралізований алгоритм пошуку
Якщо в експерименті Стенлі Мілґрема досліднику потрібно знайти саме найкоротший шлях, то йому треба відправити листи всім своїм знайомим і змусити їх зробити те ж саме. Такий «флуд» у мережі досягне мети так швидко, як тільки можливо, але така масова розсилка практично неможлива. Інший варіант експерименту — відправляти лист тільки одній людині за раз. У результаті проведення експерименту Світ тісний було скроєно разючу алгоритмічне відкриття: в графі «Світ тісний» людям, які не знають всю структуру графа, а мають тільки локальну інформацію (про своїх знайомих), вдається колективно знайти відносно короткий шлях до мети (наявність відносно короткого шляху є відомим властивістю графів типу «Світ тісний»)[42].
Виникає питання: чому соціальна мережа структурована таким чином, що такий децентралізований алгоритм пошуку дає оптимальні результати? Подібні децентралізовані алгоритми пошуку працюють також у Всесвітній павутині, в нейронних мережах і в безлічі інших областей. Отже, розуміння алгоритмів роботи децентралізованих пошукових алгоритмів забезпечить їх широке застосування[43].
Для подальших міркувань необхідно сформулювати більш суворе визначення децентралізованого алгоритму пошуку. Алгоритм рекурсивний: ми стоїмо в вершині , нам потрібно досягти вершини , ми знаємо лише сусідів вершини , серед них потрібно вибрати вершину і запустити алгоритм від неї. Децентралізований алгоритм оцінюється часом доставки — очікуваним кількістю кроків, необхідних для досягнення мети, при цьому граф «Світ тісний», стартова і цільова вершини генеруються випадковим чином. Мета досліджень — знайти полілогаріфмічні щодо алгоритми децентралізованого пошуку. Ці дослідження проводив Джон Клейнберг у роботі «Комплексні мережі та децентралізовані алгоритми пошуку».
Див. також
- [[:w::en:Erdős–Rényi model|Erdős-Rényi (ER) model]]
- [[:w::en:Watts and Strogatz Model|Watts and Strogatz Model]]
- [[:w::en:Barabási–Albert model|Barabási–Albert model]]
- Число Ердеша
- Безмасштабна мережа
- Світ тісний
- Складні мережі
- Соціальна мережа
- Число Данбара
Примітки
- Collective dynamics of small-world networks.
- Barthelmy and Amaral.
- Barrat and Weigt.
- Dorogovtsev and Mendes.
- Barmpoutis and Murray.
- Complex networks Structure and dynamics, с. 8.
- Humphries.
- Telesford, Joyce, Hayasaka, Burdette, Laurienti.
- Cohen and Havlin and ben-Avraham.
- Scale-free networks are ultrasmall.
- Proteins, с. 292–299.
- Gene network, с. 280-4.
- Che, Ali, Reynolds, 2010.
- Handbook on Biological Networks, 2010, с. 23.
- patent.
- Lamanna, Longo, 2007, с. 90.
- Designing Robust Road Networks, 2010, с. 13.
- Protein Interaction, 2006, с. 17.
- Fractals with time-delay, с. 215—219.
- Chaos in small-world networks.
- Transition to chaos.
- BarmpoutisMurray2010.
- Shirky.
- Finnegan.
- Yang.
- Jimenez, Tiampo, Posadas.
- Information Theory & Business Intelligence Strategy.
- Hillard.
- Sandberg.
- Sporns.
- Yu.
- Cohen.
- Solla.
- Humphries, с. 367-375.
- Sole.
- WordNet, с. 1.
- WordNet.
- Antiqueira, с. 4.
- Antiqueira.
- Masucci.
- Dimension of spatially embedded networks.
- Kleinberg, 2006, с. 5.
- Kleinberg, 2006, с. 6.
Джерела
- Jin Chen. Systematic Assessment of Protein Interaction Data using Graph Topology Approaches. — 2006.[недоступне посилання з травня 2019]
- Maaike Snelder. Designing Robust Road Networks A general design method applied to the Netherlands. — ISBN 978-90-5584-135-6. Архівовано 27 травня 2014 у Wayback Machine.
- Stefano Boccaletti, Vito Latora, Yamir Moreno. Handbook on Biological Networks. — ISBN 978-981-283-979-7.
- F. Lamanna and G. Longo. Connectivity and stability of the air network in the Southeastern Europe: A Small World approach // JOURNAL OF TRANSPORT AND SHIPPING. — 2007. — № 4. — ISSN 1109–9437.
- Robert Hillard (2010). Information-Driven Business. Wiley. ISBN 978-0-470-62577-4.
- Клей Ширки (2008). Here Comes Everybody. Penguin Group. с. 327. ISBN 978-1-59420-153-0.
- M. D. Humphries, K. Gurney and T. J. Prescott, Phil. Trans (2007). Is there a brainstem substrate for action selection?. R. Soc. B. doi:10.1098/rstb.2007.2057.
- K.E. Joyce, S. Hayasaka, J.H. Burdette, P.J. Laurienti (2011). The ubiquity of small-world networks Q.K. Telesford,. Brain Connect: 367–75. doi:10.1089/brain.2011.0038.
- Finnegan, William (2003). Affinity Groups and the Movement Against Corporate Globalization (англ.) 1. Wiley-Blackwell. с. 210–218. ISBN 978-0631221968. Проігноровано невідомий параметр
|издание=(довідка); Проігноровано невідомий параметр|автор издания=(довідка) - X. S. Yang (2001). Small-world networks in geophysics. Geophys. Res. Lett., 28(13): 2549—2552.
- A. Jimenez, K. F. Tiampo, A. M. Posadas (2008). Small-world in a seismic network: the California case. Nonlin. Processes Geophys., 15: 389—395.
- Jon Kleinberg. Complex networks and decentralized search algorithms. — 2006.[недоступне посилання з травня 2019]
- Xiangdong Che, M. Ali, R.G. Reynolds. Robust evolution optimization at the edge of chaos: Commercialization of culture algorithms. — 2010. — ISBN 978-1-4244-6909-3.
- Sporns, Olaf; Tononi G, Edelman GM (2004.). Organization, development and function of complex brain networks. Trends Cogn Sci. 8 (9): 418–425. PMID 15350243. doi:10.1016/j.tics.2004.07.008.
- Yu, Shan; D. Huang, W. Singer and D. Nikolić (2008). A Small World of Neuronal Synchrony. Cerebral Cortex 18 (12): 2891–2901. PMC 2583154. PMID 18400792. doi:10.1093/cercor/bhn047.
- M.Barthelemy, L.Amaral (1999). Small-world networks: Evidence for a crossover picture. Phys. Rev. Lett. 82 (15): 3180. Bibcode:1999PhRvL..82.3180B. arXiv:cond-mat/9903108. doi:10.1103/PhysRevLett.82.3180.
- R.Cohen, S.Havlin, and D.ben-Avraham (2002). Structural properties of scale free networks. Handbook of graphs and networks (Wiley-VCH, 2002) (Chap. 4).
- R. Cohen, S.Havlin (2003). Scale-free networks are ultrasmall. Phys. Rev. Lett. 90 (5): 058701. Bibcode:2003PhRvL..90e8701C. PMID 12633404. arXiv:cond-mat/0205476. doi:10.1103/PhysRevLett.90.058701.
- P.Bork, LJ Jensen, C. von Mering, A.Ramani, I.Lee, EM.Marcotte (2004). Protein interaction networks from yeast to human (PDF). Current Opinion in Structural Biology 14 (3): 292–299. PMID 15193308. doi:10.1016/j.sbi.2004.05.003.
- V.Van Noort, B.Snel, MA.Huynen (Mar 2004). The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model. EMBO Rep. 5 (3): 280–284. PMC 1299002. PMID 14968131. doi:10.1038/sj.embor.7400090.
- X. S. Yang (2002). Fractals in small-world networks with time-delay. Chaos, Solitons & Fractals 13: 215—219.
- X. S. Yang (2001). Chaos in small-world networks. Phys. Rev. E 63, 046206.
- W. Yuan, X. S. Luo, P. Jiang, B. Wang, J. Fang. Transition to chaos in small-world dynamical network. Архів оригіналу за 3 січня 2014. Процитовано 28 травня 2014.
- D.Barmpoutis and R.M. Murray (2010). Networks with the Smallest Average Distance and the Largest Average Clustering. Проігноровано невідомий параметр
|class=(довідка); Проігноровано невідомий параметр|eprint=(довідка)
- D. Li, K. Kosmidis, A. Bunde, S. Havlin (2011). Dimension of spatially embedded networks. Nature Physics. Bibcode:2011NatPh...7..481D. doi:10.1038/nphys1932.
