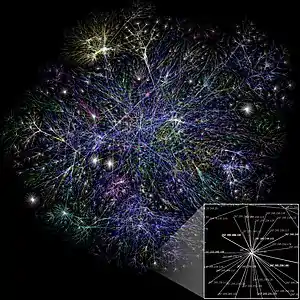
Безмасштабна мережа
Безмасшта́бна мере́жа (англ. scale-free network) — це мережа, розподіл степенів якої підкоряється степеневому законові, хоча б асимптотично. Тобто, відношення вершин (вузлів) графу мережі, що мають k зв'язків (граней), до числа усіх вершин для великих значень k визначається як
| Наука про мережі | ||||
|---|---|---|---|---|
|
||||
| Види мереж | ||||
|
||||
| Графи | ||||
|
||||
| ||||
|
||||
| Моделі | ||||
|
||||
| ||||
|
||||
де — це стала, значення якої знаходиться зазвичай у межах 2 < < 3, однак інколи значення може бути поза цими межами.
Безмасштабні мережі мають важливе значення, оскільки багато мереж, що було досліджено емпірично, є безмасштабними і включають всесвітню павутину (інтернет), мережі цитування та деякі соціальні мережі.
Основні моменти
- Безмасштабні мережі підкоряються степеневому законові розподілу степенів їхніх вузлів, як і багато реальних мереж.
- Механізм переважного приєднання було запропоновано як механізм для пояснення степенового закону розподілу степенів вершин графу безмасштабної мережі.
Історія
У дослідженні мереж цитування у наукових статтях Дерек де Солла Прайз показав у 1965 році, що число зв'язків до статей, тобто число цитувань, що отримують статті підкоряється розподілу Парето або степеневому закону, таким чином мережі цитування між статтями є безмасштабними. Прайз, однак, не використовував термін «безмасштабна мережа», який увійшов у вжиток лише через кілька десятків років. У пізнішій роботі 1976 року, Прайз також запропонував механізм для пояснення степеневого закону у мережах цитувань, який він назвав «кумулятивною перевагою», але зараз цей механізм переважно називають преференційне приєднання.
Інтерес до безмасштабних мереж спалахнув у 1999 році із появою роботи Альберта Барабасі і його колег з університету Нотр Даму. Вони накреслили топологію частин інтернету[1] і виявили що деякі вузли, які вони назвали «хаби» мали набагато більше зв'язків, ніж інші і мережа як ціле підкорялася степеневому закону розподілу зв'язків по вузлах.
Література
- Albert R. and Barabási A.-L., «Statistical mechanics of complex networks», Rev. Mod. Phys. 74, 47–97 (2002).
- Amaral, LAN, Scala, A., Barthelemy, M., Stanley, HE., «Classes of behavior of small-world networks». Proceedings of the National Academy of Sciences (USA) 97:11149-11152 (2000).
- Barabási, Albert-László Linked: How Everything is Connected to Everything Else, 2004 ISBN 0-452-28439-2
- Barabási, Albert-László «Scale-Free Networks». Scientific American, 288:60-69, May 2003.
- Barabási, Albert-László and Albert, Réka. «Emergence of scaling in random networks». Science, 286:509-512, October 15, 1999.
- Dan Braha and Yaneer Bar-Yam, «Topology of Large-Scale Engineering Problem-Solving Networks» Phys. Rev. E 69, 016113 (2004)
- Caldarelli G. «Scale-Free Networks» Oxford University Press, Oxford (2007).
- Caldarelli G., Capocci A., De Los Rios P., Muñoz M.A., «Scale-free networks from varying vertex intrinsic fitness» Physical Review Letters 89, 258702 (2002).
- Dangalchev, Ch., Generation models for scale-free networks, Physica A, 338,(2004)
- Dorogovtsev, S.N. and Mendes, J.F.F., Evolution of Networks: from biological networks to the Internet and WWW, Oxford University Press, 2003, ISBN 0-19-851590-1
- Dorogovtsev, S.N. and Mendes, J.F.F. and Samukhin, A.N., «Structure of Growing Networks: Exact Solution of the Barabási--Albert's Model», Phys. Rev. Lett. 85, 4633 (2000)
- Dorogovtsev, S.N. and Mendes, J.F.F., Evolution of networks, Advances in Physics 51, 1079—1187 (2002)
- Erdős, P. and Rényi, A. Random graphs. Publication of the Mathematical Institute of the Hungarian Academy of Science, 5, pages 17-61, 1960.
- Faloutsos, M., Faloutsos, P. and Faloutsos, C., On power-law relationships of the internet topology Comp. Comm. rev. 29, 251, 1999.
- Li, L., Alderson, D., Tanaka, R., Doyle, J.C., Willinger, W., Towards a Theory of Scale-Free Graphs: Definition, Properties, and Implications (Extended Version). Internet Mathematics, 2005.
- Kumar, R., Raghavan, P., Rajagopalan, S., Sivakumar, D., Tomkins, A., and Upfal, E.: Stochastic models for the web graph. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science (FOCS), pages 57-65, Redondo Beach, CA, USA. IEEE CS Press, 2000.
- Manev R., Manev H.; Med. Hypotheses 2005;64(1):114-7
- Matlis, Jan. Scale-Free Networks. ComputerWorld. November 4, 2002.
- Newman, Mark E. J. The structure and function of complex networks, 2003.
- Pastor-Satorras, R.,Vespignani, A.,"Evolution and Structure of the Internet: A Statistical Physics Approach", Cambridge University Press, 2004, ISBN 0-521-82698-5
- Pennock, D. M., Flake, G. W., Lawrence, S., Glover, E. J., and Giles, C. L.: Winners don't take all: Characterizing the competition for links on the web. Proceedings of the National Academy of Sciences, 99(8):5207-5211, 2002.
- Robb, John. Scale-Free Networks and Terrorism, 2004.
- Keller, E.F. Revisiting «scale-free» networks Архівовано 13 серпня 2011 у Archive.is, BioEssays 27(10) 1060—1068, 2005.
- R. N. Onody and P. A. de Castro, Complex Network Study of Brazilian Soccer Player, Phys. Rev. E 70, 037103 (2004)
- Reuven Cohen, Shlomo Havlin, «Scale-Free Networks are Ultrasmall» Phys. Rev. Lett. 90, 058701 (2003)
- Barabási and Albert 1999
Посилання
- snGraph Оптимальне програмне забезпечення для роботи із безмаштабними мережами.
- Про безмасштабні мережі на вебсайті Scholarpedia