Складні мережі
Складні мережі (англ. Complex networks) — це мережі (графи), що володіють нетривіальними топологічними властивостями. Складні мережі широко поширені у природі.
| Наука про мережі | ||||
|---|---|---|---|---|
|
||||
| Види мереж | ||||
|
||||
| Графи | ||||
|
||||
| ||||
|
||||
| Моделі | ||||
|
||||
| ||||
|
||||
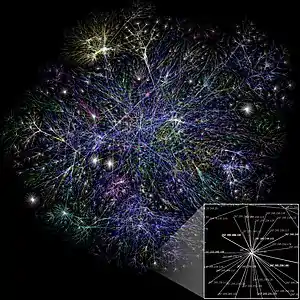
Більшість об'єктів природи і суспільства мають бінарні зв'язки, які можна представити у вигляді мережі, де кожен об'єкт це точка, а його зв'язок з іншим об'єктом це лінія або дуга.
Так відносини між людьми в групі (див. соціальна мережа), відносини між фірмами, комп'ютерні мережі, Веб, відносини між генами в ДНК — все це приклади мереж[1][2].
Топологічні властивості цих мереж (див. топологія), що розглядаються абстрактно від їх фізичної природи, але істотно визначають функціонування мереж, і становлять предмет дослідження комплексних мереж.
Основні характеристики складних мереж
Орієнтовані і неорієнтовані мережі
Кожен вузол мережі може бути пов'язаний з іншими вузлами певним числом зв'язків. Зв'язки між вузлами можуть мати напрямок. В цьому випадку мережа називається орієнтованою (англ. directed network). Якщо мережа складається із вузлів, що пов'язані між собою симетричиними зв'язками, то вона називається неорієнтованою (англ. undirected network). Наприклад, Веб це орієнтована мережа, а інтернет це неорієнтована мережа. Іноді питання про орієнтованість мережі не настільки тривіальне. Наприклад, відносини між людьми. Якщо вважати що зв'язок існує, якщо дві особи є близькими друзями, то мережа буде неорієнтованою. Якщо вважати що зв'язок існує, якщо одна особа вважає себе другом іншої, то утворена мережа буде орієнтованою.
Розподіл ступенів вузлів (англ. Degree distribution of nodes)
Число зв'язків вузла будемо називати ступенем (англ. degree) вузла. Для орієнтованих мереж розрізняють вихідні і вхідні ступеня вузла (англ. out degree та iангл. n degree). Розподіл ступенів вузлів є важливою характеристикою складної мережі. Більшість складних мереж мають близький до степеневого закону розподіл ступенів вузлів з показником ступеня між 2 і 3.
Діаметр мережі
Мінімальне число зв'язків, яке необхідно подолати, щоб потрапити з вузла у вузол, називається відстанню між вузлами. Усереднена відстань між усіма парами вузлів мережі, для яких існує шлях переходу з одного в інший, називається середньою відстанню між вузлами (або діаметром мережі) . Для більшості комплексних мереж , де — кількість вузлів у мережі.
Кластерний коефіцієнт
Будемо називати два вузли сусідніми, якщо існує зв'язок між ними. Для комплексних мереж характерно, що два вузли, які сусідні до якого-небудь вузла, часто також є сусідами між собою. Щоб охарактеризувати це явище і був запропонований кластерний коефіцієнт вузла . Припустимо, що вузол має ступінь , це означає, що у нього сусідів і між ними може бути максимум зв'язків. Тоді
де число зв'язків між сусідами вузла . Очевидно, що завжди . Усереднений кластерний коефіцієнт вузлів, називається кластерним коефіцієнтом мережі. Для більшості складних мереж він істотно більший, ніж кластерний коефіцієнт випадкового графа таких же розмірів.
Коефіцієнт асортативності
У мережі можлива ситуація, коли вузли, що мають велику ступінь (англ. hubs), переважно пов'язані з вузлами, що мають велику ступінь. Іншими словами «хаби» «воліють» бути пов'язаними з іншими «хабами». Такі мережі називають асортативними. Можлива також зворотна ситуація: «хаби» пов'язані з іншими «хабами» через ланцюжки вузлів, що мають мале число сусідів. Такі мережі називають дизасортативними. Щоб охарактеризувати цю властивість користуються коефіцієнтом асортативності (англ. Assortativity coefficient) , так називається коефіцієнт кореляції Пірсона між ступенем сусідніх вузлів. За визначенням, . Для асортативних мереж , для дизассортативних мереж . Соціальні мережі є асортативними. Мережі пов'язані з біологічними та технічними явищами найчастіше дизасортативні. Існують мережі, що не мають вираженої асортативності з близьким до нуля.
Див. також
Примітки
- Dorogovtsev SN, Mendes JFF. Evolution of Networks: From Biological Networks to the Internet and WWW. — Oxford, USA : Oxford University Press, 2003. — P. 280. — ISBN 978-0198515906.
- Mark Newman, Albert-Laszlo Barabasi, Duncan J. Watts. The Structure and Dynamics of Networks: (Princeton Studies in Complexity). — Princeton, USA : Princeton University Press, 2006. — P. 624. — ISBN 978-0691113579.
Джерела
- Ю. Головач, О. Олємской, К. фон Фербер, Т. Головач, О. Мриглод, І. Олємской, В. Пальчиков. Складні мережі. - Журн. Фіз. Досл. 10 № 4 (2006) c.247-289.
- Ландэ Д.В., Снарский А.А., Безсуднов И.В. Интернетика: Навигация в сложных сетях: модели и алгоритмы. — М. : Либроком (Editorial URSS), 2009. — 264 с. — ISBN 978-5-397-00497-8.
- Снарский А.А., Ландэ Д.В. Моделирование сложных сетей: учебное пособие. — К. : Инжиниринг, 2015. — 212 с. — ISBN 978-966-2344-44-8.
