Експонента (функція)

Експонента — показникова функція $f(x)=\exp(x)=e^{x}$ , де $e$ — число Ейлера $(e\approx 2,718)$ .

Графік експоненти

y=e^{x}

(синім).
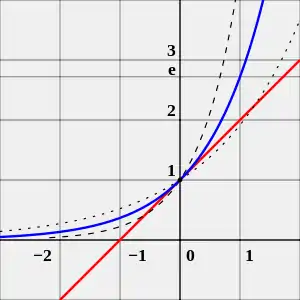
Дотична (червоним) в нулі у функції

e^{x}

нахилена на

{\frac {\pi }{4}}~(45^{\circ })

.
Поруч для прикладу показано

y=2^{x}

(точками) і

y=4^{x}

(пунктиром)

Визначення

Експоненціальна функція може бути визначена різними еквівалентними способами. Наприклад, через ряд Тейлора:

e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots

або через границю:

$e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}$

Тут $x$ — будь-яке комплексне число.

Властивості

$(e^{x})'=e^{x}$ , а зокрема, експонента — єдине рішення диференціального рівняння $y'=y$ з початковими даними $y(0)=1$ . Крім того, через експоненту виражаються загальні рішення однорідних диференціальних рівнянь.
Експонента визначена на всій дійсній осі. Вона всюди зростає і строго більше нуля.
Експонента — опукла функція.
Обернена функція до неї — натуральний логарифм $(\ln x)$ .
Фур'є-образ експоненти не існує.
Однак перетворення Лапласа існує.
Похідна в нулі дорівнює $1$ , тому дотична до експоненті в цій точці проходить під кутом $45^{\circ }~{\Big (}{\frac {\pi }{4}}{\Big )}$ .
Основна функціональна властивість експоненти, як і всякої показникової функції:
$\exp(a+b)=\exp(a)\exp(b)$ .
- Безперервна функція з такою властивістю або тотожно дорівнює $0$ , або має вигляд $\exp(cx)$ , де $c$ — деяка константа.

$e^{x}=\operatorname {sh} x+\operatorname {ch} x$ , де $\operatorname {sh}$ і $\operatorname {ch}$ — гіперболічні синус і косинус.

Комплексна експонента

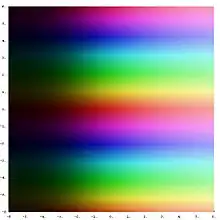
Графік експоненти в комплексній площині.
Легенда

Комплексна експонента — математична функція, що задається співвідношенням $f(z)=e^{z}$ , де $z$ є комплексне число. Комплексна експонента визначається як аналітичне продовження експоненти $f(x)=e^{x}$ речовинного змінного $x$ :

Визначимо формальний вираз

$e^{z}=e^{x+iy}=e^{x}\cdot e^{iy}$ .

Визначений таким чином вираз на дійсній осі буде збігатися з класичною дійсною експонентою. Для повної коректності побудови необхідно довести аналітичність функції $e^{z}$ , тобто показати, що $e^{z}$ розкладається в деякий збіжний ряд, що збігається до даної функції . Покажемо це:

$f(z)=e^{z}=e^{x}\cdot e^{iy}=e^{iy}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}$

Збіжність цього ряду легко доводиться:

$\left|e^{iy}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right|\leq \left|\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right|\leq \sum _{n=0}^{\infty }\left|{\frac {x^{n}}{n!}}\right|=\sum _{n=0}^{\infty }{\dfrac {|x|^{n}}{n!}}=e^{|x|}$ .

Ряд усюди збігається абсолютно, тобто взагалі усюди збігається, таким чином, сума цього ряду в кожній конкретній точці буде визначати значення аналітичної функції $f(z)=e^{z}$ . Згідно теореми єдиності, отримане продовження буде єдино, отже, на комплексній площині функція $e^{z}$ всюди визначена і аналітична.

Властивості

Комплексна експонента — ціла голоморфна функція на всій комплексній площині. В жодній точці вона не звертається в нуль.
$e^{z}$ — періодична функція з основним періодом 2π i: $e^{i\varphi }=e^{i(\varphi +2\pi )}$ . У силу періодичності комплексна експонента безкінечнолистна. В якості її області однолистності можна вибрати будь-яку горизонтальну смугу висотою $2\pi$ .
$e^{z}$ — єдина з точністю до постійного множника функція, похідна (а відповідно, і первісна) якої збігається з вихідною функцією.
Алгебраїчно експонента від комплексного аргументу $z=x+iy$ $\text{[math]}$ може бути визначена наступним чином:
$e^{z}=e^{x+iy}=e^{x}e^{iy}=e^{x}(\cos \,y+i\sin \,y)$ (формула Ейлера)
- Зокрема, має місце (тотожність Ейлера),
  $e^{i\pi }+1=0$

Варіації та узагальнення

Аналогічно експонента визначається для елемента довільної асоціативної алгебри. У конкретному випадку потрібен також доказ того, що зазначені межі існують.

Матрична експонента

Експоненту від квадратної матриці (або лінійного оператора) можна формально визначити, підставивши матрицю у відповідний ряд:

\exp A=\sum _{k=0}^{\infty }{\frac {A^{k}}{k!}}.

Визначений таким чином ряд збігається для будь-якого оператора $A$ з обмеженою нормою, оскільки мажорується поруч для експоненти норми $A:$ $\exp \|A\|.$ Отже, експонента матриці $A\in \mathbb {R} ^{n\times n}$ завжди визначена і сама є матрицею.

За допомогою матричної експоненти легко задати вид рішення лінійного диференціального рівняння з постійними коефіцієнтами: рівняння ${\dot {x}}=Ax,~~~x\in \mathbb {R} ^{n}$ з початковою умовою $x(0)=x_{0}$ має своїм рішенням $x(t)=\exp(At)x_{0}.$

h-експонента

Введення $h$ -експоненти засноване на другій чудовій границі:

$e_{h}(x)=(1+h)^{\frac {x}{h}}.$

При $h\to 0$ виходить звичайна експонента[1].

Обернена функція

Обернена функція до експоненційної функції — натуральний логарифм. Позначається $\ln x$ :

$\ln x=\log _{e}x.$

Див. також

Джерела

A.I. Olemskoi, S.S. Borysov, a, and I.A. Shuda. Statistical field theories deformed within different calculi

Література

Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.

Посилання

«Експонента і число е: просто і зрозуміло» — переклад статті An Intuitive Guide To Exponential Functions & e | BetterExplained(англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] A.I. Olemskoi, S.S. Borysov, a, and I.A. Shuda. Statistical field theories deformed within different calculi