Геометрія інцидентності
Геометрія інцидентності — розділ класичної геометрії, що вивчає структури інцидентності.
В геометрії об'єкти, такі як евклідова площина, є складними об'єктами, які використовують концепції довжин, кутів, неперервності, відношення «лежить між» і інцидентності.
Структура інцидентності — це те, що залишається, якщо відкинути усі поняття, крім даних про те, які з досліджуваних об'єктів (наприклад, точки) лежать в інших об'єктах (наприклад, колах або прямих). Навіть при таких обмеженнях деякі теореми можна довести і отримати цікаві факти щодо такої структури. Такі фундаментальні результати залишаються правильними, якщо додати інші концепції для отримання більш багатої геометрії. Іноді автори розмивають відмінність між процесом вивчення і об'єктом вивчення, так що не дивно, що деякі автори використовують для структур інцидентності назву геометрії інцидентності[1].
Структури інцидентності виникають природним чином і вивчалися в різних галузях математики. Відповідно, існує різна термінологія для опису таких об'єктів. У теорії графів вони називаються гіперграфами, а в теорії комбінаторних схем вони називаються блок-схемами. Крім різниці в термінології, в кожній галузі підхід до вивчення об'єкта відрізняється, і питання щодо об'єктів ставляться відповідно до дисципліни. Якщо використовується мова геометрії, як це робиться в геометрії інцидентності, говорять про фігури. Можливо, однак, перекласти результати з термінології однієї дисципліни на мову іншої, але часто це призводить до незграбних і заплутаних тверджень, не виглядає природно для дисципліни. У статті використано тільки приклади, що мають геометричний зміст.
Окремий випадок, що викликає великий інтерес, стосується скінченного набору точок на евклідовій площині і при цьому йдеться про кількість і типи прямих, які ці точки визначають. Деякі результати цього випадку можна поширити на більш загальні випадки, оскільки тут розглядаються тільки властивості інцидентності.
Структури інцидентності
Структура інцидентності (P, L, I) складається з множини P, елементи якої називаються точками, множини L, елементи якої називаються прямими, і відношення інцидентності I між ними, тобто підмножини P × L, елементи якої називаються прапорами[2]. Якщо (A, l) — прапор, ми кажемо, що A інцидентна l, або, що l інцидентна A (відношення симетричне), і пишемо A I l. Інтуїтивно ясно, що точка і пряма перебувають у такому відношенні тоді і тільки тоді, коли точка лежить на прямій. Якщо дано точку B і пряму m, які не утворюють прапор, то точка не лежить на прямій і пара (B, m) називається антипрапором.
Відстань у структурі інцидентності
Немає природного поняття відстані (метрики) в структурі інцидентності. Однак існує комбінаторна метрика у відповідних графах інцидентності (графах Леві), а саме, довжина найкоротшого шляху між двома вершинами в цьому двочастковому графі. Відстань між двома об'єктами структури інцидентності — двома точками, двома прямими або точкою і прямою — може бути визначена як відстань між двома відповідними вершинами в графі інцидентності структури інцидентності.
Інший шлях визначення відстані знову використовує поняття теорії графів, на цей раз використовується граф колінеарності структури інцидентності. Вершинами графа колінеарності є точки структури інцидентності і дві вершини з'єднані ребром, якщо існує пряма, інцидентна обом точкам. Відстань між двома точками структури інцидентності тоді можна визначити як відстань між ними в графі колінеарності.
Якщо відстань згадується в контексті структури інцидентності, необхідно вказувати, як відстань визначено.
Частково лінійні простори
Найбільш досліджувані структури інцидентності, це структури, що задовольняють деяким додатковим властивостями (аксіомам), такі як проєктивні площини, афінні площини, узагальнені многокутники, часткові геометрії і майже многокутники. Достатньо загальні структури інцидентності можуть бути отримані накладенням «м'яких» умов, таких як:
Частково лінійний простір є структурою інцидентності, для якої виконуються такі аксіоми[3]:
- Будь-яка пара різних точок визначає максимум одну пряму.
- Будь-яка пряма містить щонайменше дві різні точки.
У частково лінійному просторі також правильно, що будь-яка пара різних прямих перетинаються максимум в одній точці. Це твердження не включається в аксіоми, оскільки легко доводиться з першої аксіоми.
Подальші обмеження задаються умовами регулярності:
RLk: Кожна пряма інцидентна одному й тому ж числу точок. Якщо це число скінченне, воно часто позначається як k.
RPr: Кожна точка інцидентна одному й тому ж числу прямих. Якщо це число скінченне, його часто позначають як r.
З другої аксіоми частково лінійного простору слідує, що k > 1. Жодна з умов регулярності не випливає з іншої, тому слід прийняти r > 1.
Скінченний частково лінійний простір, що задовольняє обом умовам регулярності з k, r > 1, називається тактичною конфігурацією[4]. Деякі автори називають такі конфігурації просто конфігураціями[5] або проєктивними конфігураціями[6]. Якщо тактична конфігурація має n точок і m прямих, то, після подвійного підрахунку прапорів, виходить співвідношення nr = mk. Зазвичай використовується позначення (nr, mk)-конфігурація. В особливому випадку, коли n = m (а тому, r = k), замість позначення (nk, nk) часто пишуть просто (nk).
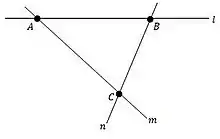
Лінійний простір є частково лінійним простором, таким, що[3]:
- Будь-яка пара різних точок визначає рівно одну пряму.
Деякі автори додають аксіому «невиродженості» (або «нетривіальності») до визначення (часткового) лінійного простору, таку як:
- Існують принаймні дві різні прямі[7].
Аксіома невиродженості дозволяє виключити деякі дуже маленькі приклади (переважно ті, в яких множини P або L складаються менш ніж з двох елементів), які були б винятками в загальних твердженнях про структури інцидентності. Альтернативний підхід — вважати структури інцидентності, що не задовольняють аксіомі невиродженості тривіальними, а ті, що задовольняють — нетривіальними.
Будь-який нетривіальний лінійний простір містить щонайменше три точки і три прямі, так що найпростіший нетривіальний лінійний простір — трикутник.
Лінійне простір, що має принаймні три точки на кожній прямій, є конфігурацією Сильвестра – Галлаї.
Основні геометричні приклади
Деякі з базових понять і термінів виникають з геометричних прикладів, особливо із проєктивних площин і афінних площин.
Проєктивні площини
Проєктивна площина — це лінійний простір, у якому:
- будь-яка пара різних прямих перетинаються рівно в одній точці;
- виконується умова невиродженості — існує чотири точки, жодні три з яких не колінеарні.
На проєктивних площинах існує бієкція між P і L. Якщо P є скінченною множиною, про проєктивну площину кажуть як про скінченну проєктивну площину. Порядок скінченної проєктивної площини дорівнює n = k – 1, тобто на одиницю менший від числа точок на прямій. Всі відомі проєктивні площини мають порядки, рівні степеню простого числа. Проєктивна площину порядку n є конфігурацією ((n2 + n + 1)n + 1).
Найменша проєктивна площина має порядок два і відома як площина Фано.
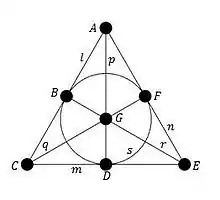
Площина Фано
Ця знаменита геометрія інцидентності була розроблена італійським математиком Джино Фано. У його роботі[8] з доведення незалежності множини аксіом для проєктивного n-простору, яку він розробляв[9], він створив скінченний тривимірний простір з 15 точками, 35 прямими і 15 площинами, в якому кожна пряма містить тільки три точки[10]. Площини в цьому просторі складаються з семи точок і семи прямих, які відомі як площини Фано.
Площина Фано не може бути подана на евклідовій площині з використанням тільки точок і відрізків (тобто нереалізовна). Це випливає з теореми Сильвестра.
Повний чотирикутник складається з чотирьох точок, жодні три з яких не колінеарні. На площині Фано три точки, що не належать повному чотирикутнику, є діагональними точками чотирикутника і колінеарні. Це суперечить аксіомі Фано, часто використовуваної в аксіоматизації евклідової площини, яка стверджує, що три діагональні точки повного чотирикутника ніколи не колінеарні.
Афінні площини
Афінна площина — це лінійний простір, у якому:
- Для будь-якої точки A і прямої l, не інцидентної точці (антипрапор), існує рівно одна пряма m, інцидентна A (тобто A I m), яка не перетинає l (аксіома Плейфера)
- Виконується умова невиродженості — існує трикутник, тобто три неколінеарні точки.
Про прямі l і m у твердженні аксіоми Плейфера кажуть як про паралельні. Будь-яка афінна площина може бути єдиним чином розширена до проєктивної площини. Порядок скінченної афінної площини дорівнює k, числу точок на прямій. Афінна площина порядку n є конфігурацією ((n2)n + 1, (n2 + n)n).
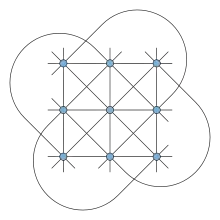
(Конфігурація Гессе)
Конфігурація Гессе
Афінна площина порядку три є конфігурацією (94, 123). Якщо конфігурація вкладена в деякий охоплювальний простір, її називають конфігурацією Гессе. Конфігурація нереалізовна на евклідовій площині, але реалізовна на комплексній проєктивній площині як дев'ять точок перегину еліптичної кривої з 12 прямими, інцидентними трійкам цих точок перегиба.
12 прямих можуть бути розбиті на чотири класи, всередині яких прямі попарно не перетинаються. Ці класи називаються класами паралельності прямих. Якщо додати ще чотири нові точки, по одній точці в кожен клас паралельності, і вважати, що всі прямі класу паралельності перетинаються в цій новій точці (таким чином, тепер всі прямі перетинаються), і додати ще одну пряму, яка містить всі чотири нові точки, отримаємо проєктивну площину порядку три, конфігурацію (134). У зворотний бік, почавши з проєктивної площини порядку три (така площина єдина) і видаливши будь-яку (одну) пряму і всі точки, що лежать на ній, отримаємо афінну площину порядку три (вона теж єдина).
Видалення однієї точки і чотирьох прямих, що проходять через неї (але не інші точки на цій прямій), отримаємо конфігурацію (83) Мебіуса — Кантора.
Часткові геометрії
%252C_the_Doily.svg.png.webp)
Якщо задано ціле число α ≥ 1, тактична конфігурація, що задовольняє аксиомі:
- Для будь-якого антипрапора (B, m) існують α прапорів (A, l), такі щоо B I l и A I m,
називається частковою геометрією. Якщо існує s + 1 точок на прямій і t + 1 прямих проходять через точку, позначення цієї часткової геометрії — pg(s, t, α).
Якщо α = 1, ці часткові геометрії є узагальненими чотирикутниками.
Якщо α = s + 1, конфігурації називаються системами Штейнера.
Узагальнені многокутники
Для n > 2[11], узагальнений n-кутник — це частково лінійний простір, граф інцидентності якого Γ має властивість:
- Обхват графа Γ (довжина найкоротшого циклу) є подвоєним діаметром графа Γ (найбільша відстань між двома вершинами, n в нашому випадку).
Узагальнений 2-кутник — це структура інцидентності, яка не є частково лінійним простором, що складається щонайменше з двох точок і двох прямих, в якій кожна точка інцидентна кожній прямій. Графом інцидентності узагальненого 2-кутника є повний двочастковий граф.
Узагальнений n-кутник не містить ніяких простих m-кутників для 2 ≤ m < n і для кожної пари об'єктів (дві точки, дві прямі або точка з прямою) існує звичайний n-кутник, що містить обидва об'єкти.
Узагальнені 3-кутники є проєктивними площинами. Узагальнені 4-сторонники називаються узагальненими чотирикутниками. За теоремою Фейта-Гіґмана існує тільки скінченне число узагальнених n-кутників щонайменше з трьома точками на кожній прямій і трьома прямими, що проходять через кожну точку, і число n дорівнює 2, 3, 4, 6 або 8.
Майже многокутники
Для невід'ємних цілих d майже 2d-кутник — це структура інцидентності, така, що:
- найбільша відстань (вимірюється за графом колінеарності) між двома точками рівна d;
- для будь-якої точки X і прямої l існує єдина точка на l, найближча до X.
Майже 0-кутник — це точка, а майже 2-кутник — пряма. Граф колінеарності майже 2-кутника — повний граф . Майже 4-кутник — це узагальнений чотирикутник (можливо, вироджений). Будь-який скінченний узагальнений многокутник, за винятком проєктивних площин, є тісним многокутником. Будь-який зв'язний двочастковий граф є майже многокутником і будь-який майже многокутник, що має рівно дві точки на кожній прямій, є зв'язним двочастинним графом. Також всі двоїсті полярні простори є майже многокутниками.
Багато майже многокутників пов'язані з скінченними простими групами, подібними до груп Матьє і групи Янко J2. Більше того, узагальнені 2d-кутники, пов'язані з групами лієвого типу, є особливими випадками майже 2d-кутників.
Площини Мебіуса
Абстрактна площина Мебіуса (або інверсна площина) — це структура інцидентності, в якій, щоб уникнути можливої плутанини з термінологією класичного випадку, прямі називають циклами або блоками.
Конкретно: площина Мебіуса — це структура інцидентності точок і циклів, така, що:
- Будь-яка трійка різних точок інцидентна рівно одному циклу.
- Для будь-якого прапора (P, z) і будь-якої точки t Q що не інцидентної z існує єдиний цикл z∗ з P I z∗, Q I z∗ і z ∩ z∗ = {P (Кажуть, що цикли торкаються P.)
- Будь-який цикл має щонайменше три точки і існує щонайменше один цикл.
Структура інцидентності, отримана з будь-якої точки P площини Мебіуса шляхом вибору як точок всіх точок, відмінних від P, а як прямих вибору тільки тих циклів, які містять P (з видаленою P), є афінною площиною. Ця структура називається залишком P в теорії схем.
Скінченна площина Мебіуса порядку m — це тактична конфігурація з k = m + 1 точками в кожному циклі, яка є 3-дизайном, блок-схемою 3-(m2 + 1, m + 1, 1)
Теореми інцидентності на евклідовій площині
Теорема Сильвестра
Питання, поставлене Д. Д. Сильвестром у 1893 році і, нарешті, доведене Тібором Галлаї, стосується інцидентності скінченного числа точок на евклідовій площині.
Теорема (Сильвестр — Галлаї): точки скінченної множини точок на евклідовій площині або колінеарні, або існує пряма, інцидентна рівно двом точкам.
Пряма, що містить рівно дві точки, називається в цьому контексті звичайною прямою. Сильвестр, можливо, прийшов до цього питання, коли обмірковував вкладаність конфігурації Гессе.
Теорема де Брейна — Ердеша
Пов'язаний результат — теорема де Брейна — Ердеша. Ніколас де Брейн і Пал Ердеш довели результат у більш загальних умовах проєктивної площини, але результат залишається правильним на евклідовій площині. Теорема гласить:[12]
- На проєктивній площині будь-яка множина n неколінеарних точок визначає щонайменше n різних прямих.
Як зазначили автори, оскільки їхнє доведення було комбінаторним, результат виконується в більш сильних умовах, фактично в будь-якій геометрії інцидентності. Вони також згадали, що версія для евклідової площини може бути доведена з теореми Сильвестра — Галлаї за допомогою індукції.
Теорема Семереді — Троттера
Границя числа прапорів, визначена скінченною множиною точок і прямих, визначається теоремою:
Теорема (Семереді — Троттер): Якщо задано n точок і m прямих на площині, кількість прапорів (пар інцидентності точка-пряма) дорівнює:
і ця границя не може бути поліпшена.
Цей результат можна використовувати для доведення теореми Бека.
Теорема Бека
Теорема Бека стверджує, що скінченні набори точок на площині розпадаються на два крайні випадки — в одних наборах всі точки лежать на одній прямій, а в інших потрібне велике число прямих для з'єднання всіх точок.
Теорема стверджує, що існують додатні константи C, K, такі, що, якщо задано n точок на площині, принаймні одне з таких тверджень істинне:
- Існує пряма, що містить щонайменше n/C точок.
- Існує щонайменше n2/K прямих, кожна з яких містить щонайменше дві точки.
В початкових доведеннях Бека C дорівнює 100, а K є невизначеною константою. Оптимальні значения C и K невідомі.
Інші приклади
- Проєктивні геометрії
- Многокутник Моуфанга
- Подвійна шістка Шлефлі
- Конфігурація Реє
- Конфігурація Кремони — Річмонда
- Конфігурація Куммера
- Конфігурація Кляйна
- Недезаргова площина
- Конфігурація (розбиття простору)
Див. також
- Комбінаторні схеми
- Скінченна геометрія
- Теорема про перетини
- Граф Леві
Примітки
- Так, наприклад, робить Л. Сторме в главі про скінченну геометрію в книзі (Colbourn, Dinitz, 2007)
- Технічно, це структура інцидентності рангу 2, де ранг стосується типів об'єктів розгляду (тут — точки і прямі). Структури вищих рангів також вивчаються, але деякі автори обмежують себе рангом 2 і ми зробимо так само.
- Moorhouse.
- Dembowski, 1968.
- Coxeter, 1969.
- Hilbert, Cohn-Vossen, 1952.
- Існує кілька альтернативних аксіом такої «нетривіальності». Аксіома може бути замінена на «існує три точки, що не лежать на одній прямій», як в книзі Баттена і Бойтельшпахера (Batten, Beutelspacher, 1993). Є інші варіанти, але у всіх має бути присутнім твердження існування, яке виключає занадто прості випадки.
- Fano, 1892.
- Collino, Conte & Verra, 2013
- Malkevitch,, Finite Geometries? an AMS Featured Column
- Використання n в імені є стандартним і не слід плутати це число з числом точок у конфігурації.
- Weisstein, Eric W., «de Bruijn–Erdős Theorem» на MathWorld
Література
- G. Fano. Sui postulati fondamentali della geometria proiettiva // Giornale di Matematiche. — 1892. — Т. 30. — С. 106–132.
- H. S. M. Coxeter. Introduction to Geometry. — New York : John Wiley & Sons, 1969. — С. 233. — ISBN 0-471-50458-0.
- David Hilbert, Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — Chelsea, 1952. — С. 94–170. — ISBN 0-8284-1087-9.
- Lynn Margaret Batten. Combinatorics of Finite Geometries. — New York : Cambridge University Press, 1986. — ISBN 0-521-31857-2.
- Lynn Margaret Batten, Albrecht Beutelspacher. The Theory of Finite Linear Spaces. — New York : Cambridge University Press, 1993. — ISBN 0-521-33317-2.
- Buekenhout, Francis (1995), Handbook of Incidence Geometry: Buildings and Foundations, Elsevier B.V.
- Charles J. Colbourn, Jeffrey H. Dinitz. Handbook of Combinatorial Designs. — 2nd. — Boca Raton : Chapman & Hall/ CRC, 2007. — ISBN 1-58488-506-8.
- Collino, Alberto; Conte, Alberto; Verra, Alessandro (2013). «On the life and scientific work of Gino Fano». arXiv:1311.7177.
- Peter Dembowski. Finite geometries. — Berlin, New York : Springer-Verlag, 1968. — Т. 44. — (Ergebnisse der Mathematik und ihrer Grenzgebiete). — ISBN 3-540-61786-8.
- Malkevitch, Joe. Finite Geometries?. Процитовано 2 грудня 2013.
- Moorhouse, G. Eric (August 2007). Incidence Geometry (pdf) (англ.). University of Wyoming. Архів оригіналу за 29 жовтня 2013. Процитовано 17 січня 2017. Проігноровано невідомий параметр
|subtitle=(довідка) - Johannes Ueberberg. Foundations of Incidence Geometry. — Springer, 2011. — (Springer Monographs in Mathematics). — ISBN 978-3-642-26960-8. — DOI:10.1007/978-3-642-20972-7..
- Ernest E. Shult. Points and Lines. — Springer, 2011. — (Universitext). — ISBN 978-3-642-15626-7. — DOI:10.1007/978-3-642-15627-4..
- Simeon Ball. Finite Geometry and Combinatorial Applications. — Cambridge University Press, 2015. — (London Mathematical Society Student Texts). — ISBN 978-1107518438..
Посилання
- Incidence system на сайті Математична енциклопедія(англ.)
