DBSCAN

DBSCAN (англ. density-based spatial clustering of applications with noise) — алгоритм кластеризації даних, який запропонували Мартін Естер (англ. Martin Ester), Ганс-Петер Крігель, Йорґ Сандер (англ. Jörg Sander) та Сяовей Су (англ. Xiaowei Xu) у 1996 році.[1] Він є алгоритмом кластеризації заснованим на щільності: для заданої множини точок у деякому просторі він відносить в одну групу точки, які розташовані найбільш щільно (точки з багатьма сусідами) та розмічає точки, які лежать в областях з невеликою щільністю (чиї сусіди розташовані занадто далеко) як викиди. DBSCAN є одним з найпоширеніших алгоритмів кластеризації, а також найбільш цитованим у науковій літературі.[2]

Частина з циклу
Машинне навчання
та добування даних
Кластерування
DBSCAN може знаходити лінійно не роздільні кластери. Цей набір даних не може бути адекватно кластеризовано методом k-середніх або ЕМ-алгоритмом.

Більш рання версія

Роберт Ф. Лінг (англ. Robert F. Ling) у 1972 році опублікував статтю «Теорія і побудова k-кластерів»[3] в журналі «The Computer Journal» з дуже близькою оцінкою часовою складністю виконання O(n³),[3] тоді, як DBSCAN має у найгіршому випадку час виконання O(n²), і DBSCAN, сформульований у вигляді орієнтованому на запити діапазонів у базу даних, дозволяє прискорити індексування. Алгоритми також відрізняються в обробці точок розташованих на межі.

Попередні визначення

Розглянемо множину точок в деякому просторі, яка будемо кластеризувати. Метою кластеризації процедурою DBSCAN є поділ точок на ядрові, (щільно-)досяжні та викиди, які визначаються так:

  • Точка p є ядровою, як хоча б minPts знаходяться на відстані ε (відстань ε є радіусом окола p) від неї, включно з p. Кажуть, що ці точки безпосередньо досяжні з p.
  • Точка q безпосередньо досяжна з p, якщо точка q знаходиться на відстані не більшій ніж ε від точки ядрової точки p.
  • Точка q є досяжною з p, якщо існує шлях p1, ..., pn з точок p1 = p та pn = q, де кожна pi+1 безпосередньо досяжна з pi (всі точки шляху повинні бути ядровими, можливо за виключенням q).
  • Всі точки не досяжні з будь-якої іншої точки є викидами.

Отже, ядрова точка p утворює «кластер» разом з усіма точками (не важливо ядрові чи ні) досяжними з неї. Кожен кластер містить принаймні одну ядрову точку. Не-ядрові точки можуть бути частиною кластера, тоді вони утворюють «ребро» кластера, оскільни з них не будуть досяжні інші точки.

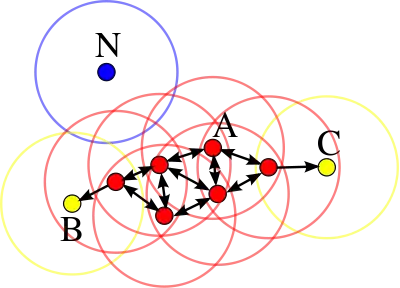
На зображенні minPts = 4. Точка A, як і червоні точки є ядровими, бо окіл цих точок радіуса ε містить щонайменше 4 точки, включно з нею самою. Оскільки, всі вони досяжні одна з одної, то вони утворюють спільний кластер.
Точки B та C не будуть ядровими, але досяжні з A або з інших ядрових точок і тому належать кластеру. Точка N є шумовою, бо не буде ні ядровою ні безпосередньо досяжною.

Досяжність не є симметричним відношенням, бо, за визначенням, немає точок досяжних з не-ядрової точки (не-ядрова точка може бути досяжною, але відносно неї немає досяжних точок). Тому, поняття зв'язності потрібне для формального визначення степені кластеризації в DBSCAN. Дві точки p та q є щільно-зв'язними, якщо існує точка o з якої вони є досяжними. Щільна-зв'язність є симетричною.

Тоді кластер має дві властивості:

  1. Всі точки кластера взаємно щільно-зв'язні.
  2. Якщо точка є щільно-зв'язно зв'язною з будь-якою точкою кластера, то вона так само належить кластеру.

Алгоритм

Початковий алгоритм на основі запитів до БД

Алгоритму DBSCAN потрібні два параметри: ε (eps) і мінімальна кількість точок необхідних для утворення щільної області[lower-alpha 1] (minPts). Побудова починається з довільної точки, яка раніше не використовувалась. Виконується запит щодо точок з ε-околу, і, якщо там буде достатньо точок, то утворюється кластер. Інакше, точка маркується як шумова. Зауважимо, що ця точка може бути знайдена пізніше в достатньо великому ε-околі іншої точки і належати кластеру, а не бути шумовою.

Якщо точка знаходиться у щільній частині кластера, то і її ε-окіл також буде частиною цього кластера. Отже, всі точки ε-околу також будуть додані у кластер, так само і ε-околи цих точок, якщо вони також будуть щільними. Цей процес продовжується доти, поки щільно-зв'язний кластер не буде знайдено повністю. Після цього виконується запит на нову необроблену точку, яка опрацьовується і, або знаходиться новий кластер, або вона позначається як шумова.

Алгоритм DBSCAN можна використовувати з будь-якою функцією відстані[1][4] (так само, як функції подібності або інші предикати).[5] Тому можна розглядати функцію відстані (dist) як додатковий параметр.

Алгоритм записаний на псевдокоді буде виглядати так:[4]

DBSCAN(DB, distFunc, eps, minPts) {
   C = 0                                                  /* Лічильник міток кластерів */
   for each point P in database DB {
      if label(P) ≠ undefined then continue               /* Раніше оброблено у внутрішньому циклі */
      Neighbors N = RangeQuery(DB, distFunc, P, eps)      /* Пошук сусідів */
      if |N| < minPts then {                              /* Перевірка щільності */
         label(P) = Noise                                 /* Позначається як Шум */
         continue
      }
      C = C + 1                                           /* Мітка наступного кластера */
      label(P) = C                                        /* Помічаємо початкову точку */
      Seed set S = N \ {P}                                /* Множина з сусідів для перевірки */
      for each point Q in S {                             /* Обробляємо кожну точку */
         if label(Q) = Noise then label(Q) = C            /* Зміна з Шум на граничну точку */
         if label(Q) ≠ undefined then continue            /* Раніше оброблені */
         label(Q) = C                                     /* Помічається сусід */
         Neighbors N = RangeQuery(DB, distFunc, Q, eps)   /* Пошук сусідів */
         if |N| ≥ minPts then {                           /* Перевірка щільності */
            S = S ∪ N                                     /* Додаємо нових сусідів у множину для перевірки */
         }
      }
   }
}

Тут RangeQuery може бути реалізована за допомогою індексування бази даних для кращої швидкодії або можна використати повільний лінійний пошук:

RangeQuery(DB, distFunc, Q, eps) {
   Neighbors = empty list
   for each point P in database DB {                      /* Перебираємо всі точки в базі */
      if distFunc(Q, P) ≤ eps then {                      /* Обчислюємо відстань і порівнюємо з епсилон */
         Neighbors = Neighbors ∪ {P}                      /* Додаємо до результату */
      }
   }
   return Neighbors
}

Абстрактний алгоритм

Алгоритм DBSCAN можна абстрактно описати наступними кроками:[4]

  1. Знайти точки у кожному ε-околі кожної точки та визначити ядрові точки, у яких більше ніж minPts сусідів.
  2. Знайти компоненти зв'язності для ядрових точок на графі сусідів, виключивши з розгляду точки, які не є ядровими.
  3. Приєднати кожну не ядрову точку до найближчого кластера, за умови, що кластер знаходиться в ε (eps) околі, інакше помітити її як шумову.

Наївна реалізація потребує зберігання списку сусідів на кроці 1, тому потрібно використовувати суттєвий об'єм пам'яті. Оригінальний алгоритм DBSCAN не потребує цього, бо виконує ці кроки для однієї точки за раз.

Складність

DBSCAN сканує кожну точку бази, можливо, навіть декілька разів. Наприклад, коли це кандидати до різних кластерів. Однак, з практичної точки зору, часова складність визначається кількістю запитів regionQuery. DBSCAN робить рівно один запит для кожної точки і, якщо використовувати просторовий індекс при пошуку сусідів, то можна це виконувати за час O(log n). Тоді можна досягти середньої часової складності O(n log n) за умови вибору параметру ε у такий спосіб, щоб запит повертав у середньому O(log n) точок. Без використання такого прискорення з просторовим індексом або для вироджених даних (коли всі точки на відстані меншій ніж ε), у найгіршому випадку часова складність буде O(n²). Матриця відстаней розміру (n²-n)/2 можна зберігати у пам'яті розміру O(n²), без використання матриці відстаней, реалізація DBSCAN потребує лише O(n) пам'яті.

Переваги
  1. Не потрібно вказувати апріорну кількість кластерів, як це потрібно для методу k-середніх.
  2. Знаходить кластери довільної форми. Може навіть знаходити кластер повністю оточений (але не лінійно зв'язний) іншим кластером. За допомогою параметру MinPts можна позбутись ефекту одного зв'язку, коли різні кластери зв'язані тонкою лінією.
  3. Має поняття шуму, і є надійним для виявлення аномалій.
  4. Потребує всього два параметри і здебільшого нечутливий до впорядкування точок. (Однак, точки розташовані на границі двох різних кластерів можуть змінити належність кластерам, якщо поміняти їх порядок у базі.)
  5. Призначений для використання з базами даних, які можуть прискорити регіональні запити, наприклад, використовують R*-дерево.
  6. Параметри minPts та ε можуть бути визначені профільним експертом, якщо дані зрозумілі.

Недоліки
  1. DBSCAN не є детерміністичним: точки на межі, які досяжні з декількох кластерів, можуть належати одному або іншому кластеру в залежності від порядку обробки даних. Для більшості наборів даних та областей, така проблема з'являється рідко і має незначний вплив на результат кластеризації,[4] бо шумові та ядрові точки визначаються однозначно. DBSCAN*[6] класифікує точки на межі як шум, що робить алгоритм детерміністичним і більш статистично узгоджену інтерпретацію компонент.
  2. Якість кластеризації залежить від функції відстані, яка використовується у функції regionQuery(P,ε). Зазвичай використовується евклідова відстань. Особливо при кластеризації багатовимірних даних ця метрика може стати негодящою через так зване «прокляття розмірності», що ускладнює пошук придатного значення для ε. Цей ефект, однак, присутній і в будь-якому іншому алгоритмі кластеризації, який використовує евклідову відстань.
  3. Не може кластеризувати набори даних з великим перепадом щільностей, оскільки неможливо підібрати поєднання значень minPts-ε, яке б відповідало різним кластерам.[7]
  4. Якщо дані та масштаб не дуже зрозумілі, то вибір доречного порогового значення відстані ε може бути складним.

Дивись розділ нижче про модифікації алгоритму, які вирішують ці вади.

Оцінка параметрів

Кожна задача добування даних має проблему визначення параметрів. Кожен параметр впливає специфічним чином. Для DBSCAN потрібно визначати параметри ε та minPts. Ці параметри повинні бути визначені користувачем. В ідеальній ситуації значення ε визначається з проблеми, яка розв'язується (наприклад, це може бути фізична відстань), а minPts визначається з бажаного мінімального розміру кластера.[lower-alpha 1]

  • MinPts: Як правило мінімальне значення параметру можна обчислити залежно від кількості вимірів D набору даних. А саме, minPts ≥ D + 1. Найменше значення minPts = 1, очевидно, не має сенсу, бо тоді кожна точка утворить кластер. При minPts ≤ 2, результат буде такий же самий, які і при ієрархічній кластеризації, тільки дерево буде обмежено висотою ε. Тому, щонайменшим значенням minPts буде 3. Однак, краще брати більші значення, як для наборів даних з шумами, так і для побудови більш вагомих кластерів. Як правило вибирають minPts = 2·dim,[5] але можливо слід використовувати і більші значення для дуже великих даних, або для зашумлених даних або даних з великою кількістю дублікатів.[4]
  • ε: Значення для ε можна вибрати за допомогою графу k-відстані виводячи відстань по графіку для k = minPts-1 найближчих сусідів впорядкованих від найбільшого до найменшого значення.[4] Гарним значення ε відповідає точці на графіку, де утворюється «згин»:[1][5][4] якщо ε вибрано занадто малим, то велика частина даних не буде кластерізована; якщо ж ε буде занадто великим, то кластери зіллються і різні об'єкти опиняться в одному кластері. Загалом, краще брати невеликі значення ε,[4] бо, як правило, тільки невеликі частини даних повинні бути в межах цієї відстані один від одного. Крім того, можна використати алгоритм OPTICS для вибору ε,[4] але тоді можна його застосувати і для кластеризації даних.
  • Функція відстані: Вибір функції відстані тісно пов'язаний з вибором ε, і має значний вплив на результати. Загалом, перш за все необхідно визначити розумну міру подібності для набору даних, перш ніж вибирати параметр ε. Для цього параметра немає оцінок, але функцію відстані слід обирати відповідно до набору даних. Наприклад, для географічних даних, відстань, яка вимірюється по великому колу, є найбільш прийнятною.

OPTICS можна розглядати як узагальнення DBSCAN, який замінює параметр ε максимальним значенням, що найбільше впливає на швидкодію. MinPts по суті стає мінімальним розміром кластера. Хоча цей алгоритм набагато простіше параметризувати, ніж DBSCAN, його результати трохи важче використати ніж результати DBSCAN, бо він будує ієрархічну кластеризацію замість простого розбиття даних, як це робить DBSCAN.

Нещодавно, один з авторів DBSCAN переглянув роботу DBSCAN та OPTICS, й оприлюднив удосконалену версію ієрархічного алгоритму DBSCAN (HDBSCAN*),[6] яка вже не використовує поняття точок на межі. Натомість, кластер утворюють лише ядрові точки.

Узагальнення

DBSCAN (GDBSCAN)[5][8] був узагальнений тими ж авторами на довільні предикати «окіл» та «щільність». Параметри ε та minPts були переміщені з алгоритму у ці предикати. Наприклад, для даних на багатокутнику, поняття «сусідні» можна сприймати, як такі, що мають перетин, а поняття щільності використовує площі полігонів замість підрахування кількості об'єктів.

Пропонуються різні методи розширення алгоритму DBSCAN, такі як розпаралелювання, оцінка параметрів та підтримка невизначених даних. Основна ідея була розповсюджена на ієрархічну кластеризацію за допомогою алгоритму OPTICS. DBSCAN також використовується як складова частина алгоритмів підпросторової кластеризації, таких як PreDeCon і SUBCLU. HDBSCAN[6] — це ієрархічний варіант DBSCAN, швидший за OPTICS, в якому можна отримати розбиття на найбільші кластери з ієрархії.[9]

Реалізації

З'ясувалось, що різні реалізації одного й того ж алгоритму мають дуже велику різницю у швидкодії. На тестовому наборі даних найшвидший виконувався 1,4 секунди, а найповільніший 13803 секунди.[10] Таку різницю можна пояснити якістю реалізації, вибором мови програмування та відмінностями у компіляторах, і використанням індексів для пришвидшення.

  • Apache Commons Math містить реалізацію на Java, яка виконується за квадратичний час.
  • ELKI має різні реалізації DBSCAN, такі як GDBSCAN та інші. Ця реалізація може використовувати різні структури індексу для досягнення доквадратичного часу виконання. Також вона підтримує довільні функції відстані та довільні типи даних, але це можна перевершити, якщо використати низькорівневу оптимізацію (та спеціалізацію) орієнтуючись на невеликі набори даних.
  • R містить DBSCAN у пакеті fpc з підтримкою довільних функцій відстані як матриці відстаней. Проте не підтримує індекси (тому має квадратичний час виконання та об'єм пам'яті) та є досить повільним через R-інтерпретатор. Швидша версія реалізована на C++ з використанням k-вимірних дерев (тільки для евклідової відстані) в R-пакеті dbscan.
  • scikit-learn включає реалізацію DBSCAN на мові Python для довільної відстані Мінковського, яка може бути пришвидшена за допомогою k-вимірних дерев та ball tree, але вони використовують у найгіршому випадку квадратичну пам'ять. Наявна реалізація алгоритму HDBSCAN*.
  • Бібліотека pyclustering містить реалізації на мовах Python та C++ тільки для евклідової відстані, так само, як і для алгоритму OPTICS.
  • SPMF містить реалізацію DBSCAN з підтримкою k-вимірних дерев тільки для евклідової відстані.
  • Weka містить (як опціональний пакет у більш пізніх версіях) базову реалізацію DBSCAN, яка виконується за квадратичний час та потребує лінійної пам'яті.

Примітки
  1. Інтуїтивно minPts відповідає мінімальному розміру кластера, але в деяких випадках DBSCAN може утворювати й менші кластери.[4] Кластери DBSCAN містять щонайменше одну ядрову точку.[4] Оскільки інші точки можуть бути на межі більш ніж одного кластера, тому немає гарантії, що принаймні minPts точок буде у кожному кластері.

Посилання
  1. Ester, Martin; Kriegel, Hans-Peter; Sander, Jörg; Xu, Xiaowei (1996). У Simoudis, Evangelos; Han, Jiawei; Fayyad, Usama M. A density-based algorithm for discovering clusters in large spatial databases with noise Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). AAAI Press. с. 226–231. ISBN 1-57735-004-9. Проігноровано невідомий параметр |citeseerx= (довідка)
  2. Archived copy. Архів оригіналу за 21 квітня 2010. Процитовано 18 квітня 2010. Найбільш цитовані статті по добуванню даних згідно з сервісом Microsoft академічного пошуку DBSCAN має рейтинг 24.
  3. Ling, R. F. (1 січня 1972). On the theory and construction of k-clusters. The Computer Journal (англ.) 15 (4): 326–332. ISSN 0010-4620. doi:10.1093/comjnl/15.4.326.
  4. Schubert, Erich; Sander, Jörg; Ester, Martin; Kriegel, Hans Peter; Xu, Xiaowei (July 2017). DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. 42 (3): 19:1–19:21. ISSN 0362-5915. doi:10.1145/3068335.
  5. Sander, Jörg; Ester, Martin; Kriegel, Hans-Peter; Xu, Xiaowei (1998). Density-Based Clustering in Spatial Databases: The Algorithm GDBSCAN and Its Applications. Data Mining and Knowledge Discovery (Berlin: Springer-Verlag) 2 (2): 169–194. doi:10.1023/A:1009745219419.[недоступне посилання]
  6. Campello, Ricardo J. G. B.; Moulavi, Davoud; Zimek, Arthur; Sander, Jörg (2015). Hierarchical Density Estimates for Data Clustering, Visualization, and Outlier Detection. ACM Transactions on Knowledge Discovery from Data 10 (1): 1–51. ISSN 1556-4681. doi:10.1145/2733381.
  7. Kriegel, Hans-Peter; Kröger, Peer; Sander, Jörg; Zimek, Arthur (2011). Density-based Clustering. WIREs Data Mining and Knowledge Discovery 1 (3): 231–240. doi:10.1002/widm.30.
  8. Sander, Jörg (1998). Generalized Density-Based Clustering for Spatial Data Mining. München: Herbert Utz Verlag. ISBN 3-89675-469-6.
  9. Campello, R. J. G. B.; Moulavi, D.; Zimek, A.; Sander, J. (2013). A framework for semi-supervised and unsupervised optimal extraction of clusters from hierarchies. Data Mining and Knowledge Discovery 27 (3): 344. doi:10.1007/s10618-013-0311-4.
  10. Kriegel, Hans-Peter; Schubert, Erich; Zimek, Arthur (2016). The (black) art of runtime evaluation: Are we comparing algorithms or implementations?. Knowledge and Information Systems 52 (2): 341. ISSN 0219-1377. doi:10.1007/s10115-016-1004-2.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.