Адіабатичний процес
Адіаба́тний проце́с (грец. αδιαβατος — неперехідний) — в термодинаміці зміна стану тіла без обміну теплом з навколишнім середовищем. Його можна здійснити, проводячи стискання чи розширення тіла (наприклад, газу) дуже швидко.
| Частина серії статей на тему: | ||||||||
| Термодинаміка | ||||||||
|---|---|---|---|---|---|---|---|---|
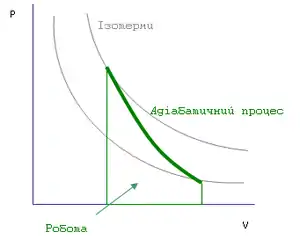 Графік адіабатичного процесу | ||||||||
|
Розділи |
||||||||
|
||||||||
|
Властивості
|
||||||||
|
Властивості матерії
|
||||||||
|
Рівняння
|
||||||||
|
Історія
|
||||||||
|
| ||||||||
Так, при поширенні звукових хвиль у повітрі чи іншому тілі, у місцях згущення частинок температура підвищується, а в місцях розрідження — знижується. За дуже малий період коливання не відбувається помітного обміну теплом між місцями згущення і розрідження.
Під час адіабатного стискування тіла внутрішня енергія його збільшується, а при адіабатному розширенні — зменшується. Виконана робота при цьому дорівнює за величиною і протилежна за знаком зміні внутрішньої енергії системи.
Адіабатні процеси в атмосфері
Адіабатне розширення потоку нагрітого повітря і ненасиченої пари з нижніх до верхніх прошарків атмосфери є основною причиною зниження потоку, конденсації водяної пари та утворення хмар. При опусканні повітряних мас відбувається зворотний адіабатний процес, внаслідок якого температура підвищується. На адіабатне нагрівання й охолодження повітря в атмосфері накладаються ще й теплові ефекти, спричинювані тепловим випромінюванням, теплопровідністю, конвекцією, а також випаровуванням та конденсацією. В сухому та ненасиченому повітрі зниження чи підвищення температури на кожні 100 м дорівнює 1,0 °C. У повітрі, насиченому водяною парою — приблизно 0,5 °C.
Формули
Математично адіабатний процес описується рівнянням
де p — тиск, V — об'єм, — показник адіабати,
— молярна теплоємність за умов постійного тиску, а — молярна теплоємність за умов сталого об'єму. Для одноатомного ідеального газу, , а для двоатомних (таких як азот або кисень, головних складових повітря) . Цю формулу можна застосовати лише для класичних газів.
Для адіабатного процесу теплообмін з навколишнім середовищем відсутній, тобто кількість теплоти . Тоді, відповідно до першого закону термодинаміки:
де E — внутрішня енергія системи, а W — робота, що виконується самою системою. Будь-яка робота (W) здійснюється за рахунок витрат внутрішньої енергії E, адже надходження теплоти ззовні немає. Робота W, що виконується системою визначається як
Однак p не залишається сталим в адіабатному процесі, а змінюється разом з V. Бажано знати, як величини та співвідносяться між собою в адіабатному процесі. Припустимо тепер, що в нас є одноатомний газ, тоді
де R — універсальна газова стала.
Нехай задані та . Відповідно . Використовуючи рівняння стану ідеального газу надамо внутрішній енергії наступного вигляду
- Тут — стала Больцмана, N — кількість атомів у системі. Тепер підставимо вирази для енергії і роботи в перший закон термодинаміки. У висліді отримаємо:
- .
Після спрощення
Розділимо обидві частини на ,
Останнє рівняння можна розглядати як диференційне рівняння з відокремленими змінними. Його можна записати і так
- .
- Загальний інтеграл цього рівняння має вигляд
- ,
- де C — довільна стала. Її можна знайти з початкової умови, якщо вважати, що у початковий момент часу газ мав тиск і об'єм , тобто з умови
- .
Тоді частинний інтеграл рівняння можна записати так
- ,
або
- або
- ,
- або
- ,
або
- ,
або
Адіабата
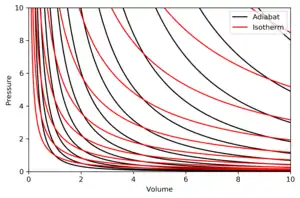
Графік на діаграмі залежності тиску від об'єму при адіабатичному процесі називається адіабатою[1].
Властивості адіабат на p-V-діаграмах такі:
- кожна адіабата асимптотично досягає як осі V, так і осі p (як і ізотерми).
- кожна адіабата перехрещується з кожною ізотермою тільки в одній точці.
- адіабата виглядає схожою на ізотерму, за винятком того, що при адіабатному розширенні втрачається більше тиску ніж при ізотермічному, тому вона має більший ухил (більш «вертикальна»).
На рисунку зображено p-V-діаграму з суперпозицією адіабат та ізотерм.
Використання терміну «адіабатний»
Термін використовується в різних значеннях, тому в кожному випадку потрібні уточнення.
- 1. У термодинаміці адіабатний використовується в макроскопічному сенсі і стосується процесу, що відбувається в термічно ізольованій системі.
- 2. У динаміці хімічних реакцій адіабатний використовується в мікроскопічному сенсі, що практично має мало спільного з його термодинамічним значенням. Тоді, коли в термодинамічному сенсі розуміють умови, які накладаються на
процес спостерігачем, мікроскопічний сенс стосується умов, при яких процес відбувається природно. При описі динаміки реакцій вважається, що квантовий стан залишається незмінним протягом усього шляху реакції. Тут можливі такі варіанти:
— реакція, в якій не відбувається зміни електронного стану або мультиплетності (називається адіабатною або електронно адіабатною);
— реакція, в якій не відбувається зміни коливального стану протягом її перебігу, зветься коливально адіабатною; менш строго цей вираз застосовується до процесів, в яких надлишок коливальної енергії в реактантах з'являється як коливальна енергія в продуктах або в яких основний коливальний стан у реактантах приводить до основного коливального стану в продуктах;
— реакція, в якій надлишок обертальної енергії в реактантах проявляється як обертальна енергія в продуктах, або в якій основний обертальний стан реактантів дає основний обертальний стан продуктів (називається обертально адіабатною);
— у теорії мономолекулярних реакцій Райса — Рамспергера — Касселя — Маркуса (РРКМ) ступінь свободи, квантове число якого зберігається сталим впродовж зростання енергії та наступної реакції (називають адіабатним, так називають тоді і саму реакцію).
- 3. Реакція, яка не є адіабатною (називається неадіабатною чи діабатною).
Див. також
Примітки
Література
- Якібчук П. М., Клим М. М. Молекулярна фізика. — Львів: Львівський національний університет імені Івана Франка, 2015.
- Козицький С. В., Золотко А. Н. Курс загальної фізики, Том 2. Молекулярна фізика. — Одеса: Астропринт, 2011.
- Глосарій термінів з хімії // Й. Опейда, О. Швайка. Ін-т фізико-органічної хімії та вуглехімії ім. Л. М. Литвиненка НАН України, Донецький національний університет. — Донецьк: Вебер, 2008. — 758 с. — ISBN 978-966-335-206-0