Вага (теорія представлень)

Приклад ваг представлення алгебри Лі sl(3,C)

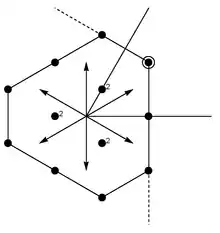
Нехай V — представлення алгебри Лі ${\displaystyle {\mathfrak {g}}}$ над алгебрично замкнутим полем F і λ — лінійний функціонал на ${\displaystyle {\mathfrak {h}}}$. Тоді ваговим простором V з вагою λ називається підпростір ${\displaystyle V_{\lambda }}$ за означенням рівний

${\displaystyle V_{\lambda }:=\{v\in V:\forall H\in {\mathfrak {h}},\quad H\cdot v=\lambda (H)v\}}$.

Вагою представлення V називається лінійний функціонал λ для якого ваговий простір є ненульовим. Ненульові елементи вагового простору називаються ваговими векторами. Вагові вектори є одночасно власними векторами для дії усіх елементів ${\displaystyle {\mathfrak {h}}}$. Відповідні власні значення задає функціонал λ.

Множина

${\displaystyle V'=\bigoplus _{\lambda \in {\mathfrak {h}}^{*}}V_{\lambda }}$

є прямою сумою різних вагових просторів і V' є підмодулем V. Якщо V = V' то V називається ваговим модулем. Зокрема у випадку скінченновимірних представлень V завжди є рівним прямій сумі своїх вагових просторів. Звідси випливає також скінченність множини ваг у цьому випадку.

Якщо V є приєднаним представленням алгебри ${\displaystyle {\mathfrak {g}}}$ то ненульові ваги V називаються коренями, вагові простори називаються кореневими просторами, а вагові вектори - кореневими векторами. А саме, лінійний функціонал ${\displaystyle \alpha }$ на ${\displaystyle {\mathfrak {h}}}$ називається коренем, якщо ${\displaystyle \alpha \neq 0}$ і існує ненульовий ${\displaystyle X}$ у ${\displaystyle {\mathfrak {g}}}$ для якого

${\displaystyle [H,X]=\alpha (H)X}$

для всіх ${\displaystyle H}$ у ${\displaystyle {\mathfrak {h}}}$. Корені напівпростої алгебри Лі утворюють систему коренів у абстрактному означенні.

Система коренів повністю визначає відповідну напівпросту алгебру Лі і використовується для їх класифікації. Для теорії представлень основне значення має такий результат: Якщо V є представленням ${\displaystyle {\mathfrak {g}}}$, v є ваговим вектором з вагою ${\displaystyle \lambda }$ і X — кореневим вектором з коренем ${\displaystyle \alpha }$, то

${\displaystyle H\cdot (X\cdot v)=[(\lambda +\alpha )(H)](X\cdot v)}$

для всіх H у ${\displaystyle {\mathfrak {h}}}$. Тобто ${\displaystyle X\cdot v}$ є або нульовим вектором або ваговим вектором з вагою ${\displaystyle \lambda +\alpha }$. Тобто при дії ${\displaystyle X}$ ваговий простір з вагою ${\displaystyle \lambda }$ відображається у ваговий простір з вагою ${\displaystyle \lambda +\alpha }$.

Цілочислові елементи (трикутна ґратка), домінантні цілочислові елементи (чорні точки), і фундаментальні ваги для sl(3,C)

Нехай ${\displaystyle {\mathfrak {h}}_{0}^{*}}$ — дійсний простір ${\displaystyle {\mathfrak {h}}^{*}}$ що є дійсною оболонкою коренів ${\displaystyle {\mathfrak {g}}}$. Введемо на ньому скалярний добуток одержаний із форми Кіллінга. Вся ця побудова має зміст оскільки усі значення форми Кіллінга на коренях є раціональними числами і форму можна лінійно поширити на дійсну лінійну оболонку отримавши при цьому скалярний добуток. Цей скалярний добуток також буде інваріантним щодо групи Вейля, яка є породженою відбиттями щодо гіперплощин ортогональних до коренів. За допомогою скалярного добутку можна ідентифікувати ${\displaystyle {\mathfrak {h}}_{0}^{*}}$ із відповідним простором ${\displaystyle {\mathfrak {h}}_{0}}$. Також можна ввести поняття кокореня для кореня ${\displaystyle \alpha }$ як

${\displaystyle H_{\alpha }=2{\frac {\alpha }{\langle \alpha ,\alpha \rangle }}}$.

Елемент ${\displaystyle \lambda \in {\mathfrak {h}}_{0}}$ називається цілочисловим якщо

${\displaystyle \langle \lambda ,H_{\alpha }\rangle =2{\frac {\langle \lambda ,\alpha \rangle }{\langle \alpha ,\alpha \rangle }}\in \mathbf {Z} }$

для всіх коренів ${\displaystyle \alpha }$. Мотивацією для цієї умови є те що кокорінь ${\displaystyle H_{\alpha }}$ можна ідентифікувати із елементом H у стандартній базі ${\displaystyle {X,Y,H}}$ для sl(2,F)-підалгебри у g.[1] Відповідно до стандартних результатів для sl(2,F), власні значення ${\displaystyle H_{\alpha }}$ для будь-якого скінченновимірного представлення є цілими числами. Тому вага будь-якого скінченновимірного представлення ${\displaystyle {\mathfrak {g}}}$ є цілочисловою.[2]

Фундаментальними вагами ${\displaystyle \omega _{1},\ldots ,\omega _{n}}$ називаються ваги, що утворюють базис у ${\displaystyle {\mathfrak {h}}_{0}}$ що є двоїстим до множини кокоренів, що відповідають простим кореням. Тобто фундаментальні ваги задаються умовами

${\displaystyle 2{\frac {\langle \omega _{i},\alpha _{j}\rangle }{\langle \alpha _{j},\alpha _{j}\rangle }}=\delta _{i,j}}$

де ${\displaystyle \alpha _{1},\ldots \alpha _{n}}$ є простими коренями. Елемент ${\displaystyle \lambda }$ є цілочисловим, якщо і тільки якщо він є цілочисловою комбінацією фундаментальних ваг.[3] Множина всіх ${\displaystyle {\mathfrak {g}}}$-цілочислових ваг є ґраткою у ${\displaystyle {\mathfrak {h}}_{0},}$ що називається ваговою ґраткою для ${\displaystyle {\mathfrak {g}}}$ і позначається ${\displaystyle P({\mathfrak {g}})}$.

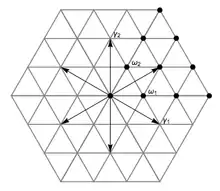
На малюнку зображено приклад алгебри Лі sl(2,F), система коренів якої є системою ${\displaystyle A_{2}}$. У цьому випадку є два прості корені, ${\displaystyle \gamma _{1}}$ і ${\displaystyle \gamma _{2}}$. Перша фундаментальна вага, ${\displaystyle \omega _{1}}$, є ортогональною до ${\displaystyle \gamma _{2}}$ і ортогонально відображається на половину ${\displaystyle \gamma _{1}}$; подібні властивості також виконуються для ${\displaystyle \omega _{2}}$. Ваговою ґраткою у цьому випадку є трикутна ґратка.

Якщо алгебра Лі ${\displaystyle {\mathfrak {g}}}$ є алгеброю Лі групи Лі G то ${\displaystyle \lambda \in {\mathfrak {h}}_{0}}$ називається аналітично цілочисловим (G-цілочисловим) елементом якщо кожен t у ${\displaystyle {\mathfrak {h}}}$ для якого ${\displaystyle \exp(t)=1\in G}$ задовольняє властивість ${\displaystyle \langle \lambda ,t\rangle \in 2\pi i\mathbf {Z} }$. Якщо представлення ${\displaystyle {\mathfrak {g}}}$ є диференціалом представлення G, тоді будь-яка вага представлення буде G-цілочисловою.[4] Для напівпростої групи G множина всіх G-цілочислових ваг є підґраткою P(G) ⊂ P(${\displaystyle {\mathfrak {g}}}$). Якщо G є однозв'язною, то P(G) = P(${\displaystyle {\mathfrak {g}}}$). Якщо G не є однозв'язною, то ґратка P(G) є меншою P(${\displaystyle {\mathfrak {g}}}$) і їх факторгрупа є ізоморфною фундаментальній групі G.[5]

На множині ваг можна ввести часткове упорядкування, яке використовується при описі і класифікації представлень алгебри g. Нехай R — множина коренів і ${\displaystyle R^{+}}$ — додатні корені.

Нехай ${\displaystyle \mu }$ і ${\displaystyle \lambda }$ — два елементи у ${\displaystyle {\mathfrak {h}}_{0}}$. Елемент ${\displaystyle \mu }$ називається вищим або старшим, ніж ${\displaystyle \lambda }$ (позначається ${\displaystyle \mu \succeq \lambda }$), якщо ${\displaystyle \mu -\lambda }$ є лінійною комбінацією додатних коренів із невід'ємними цілими коефіцієнтами.[6]

Цілочисловий елемент λ називається домінантним якщо ${\displaystyle \langle \lambda ,\gamma \rangle \geq 0}$ для кожного додатного кореня γ. Еквівалентно, λ є домінантним якщо він є невід'ємною цілочисловою комбінацією фундаментальних ваг. У випадку ${\displaystyle A_{2}}$, домінантні цілочислові елементи належать сектору із кутом 60 градусів.

Множина всіх λ (не обов'язково цілочислових) для яких ${\displaystyle \langle \lambda ,\gamma \rangle \geq 0}$ називається замкнутою фундаментальною камерою Вейля асоційованою із даною множиною додатних коренів.

Вага ${\displaystyle \lambda }$ представлення ${\displaystyle V}$ алгебри ${\displaystyle {\mathfrak {g}}}$ називається старшою вагою якщо кожна інша вага ${\displaystyle V}$ є меншою, ніж ${\displaystyle \lambda }$.

Представлення (не обов'язково скінченновимірне) V ${\displaystyle {\mathfrak {g}}}$ називається модулем найвищої ваги якщо воно є породжене ваговим вектором v ∈ V який переходить у нуль при дії будь-якого додатного кореневого вектора у ${\displaystyle {\mathfrak {g}}}$. Кожен незвідний ${\displaystyle {\mathfrak {g}}}$-модуль із старшою вагою є модулем старшої ваги, але у нескінченновимірному випадку, модуль старшої ваги може не бути незвідним.

Теорія незвідних представлень алгебри ${\displaystyle {\mathfrak {g}}}$ значною мірою будується на ідеї старшої ваги. Ключовим результатом тут є теорема про старшу вагу, яка стверджує що

(1) Для кожного незвідного скінченновимірного представлення існує старша вага,

(2) Старша вага є завжди домінантним, цілочисловим елементом,

(3) Два незвідні (можливо нескінченновимірні) представлення із однаковою старшою вагою є ізоморфними,

(4) Кожен елемент є старшою вагою деякого незвідного представлення,

(5) Представлення зі старшою вагою є скінченновимірним тоді і тільки тоді коли ця вага є цілочисловою і домінантною. Таким чином існує ізоморфізм між домінантними цілочисловими вагами і класами ізоморфізму скінченновимірних незвідних представлень алгебри Лі.

Якщо ${\displaystyle \lambda }$ є вагою деякого незвідного скінченновимірного представлення, а ${\displaystyle \alpha }$— коренем алгебри Лі, то існують цілі числа ${\displaystyle r\geqslant 0\geqslant q}$ для яких ${\displaystyle r-q=2{\frac {\langle \lambda ,\alpha \rangle }{\langle \alpha ,\alpha \rangle }}}$ і всі лінійні функціонали виду ${\displaystyle \lambda +i\alpha ,\;\;r\geqslant i\geqslant q}$ є вагами, тобто утворюється неперервна послідовність елементи якої відрізняються на ${\displaystyle \alpha }$. До того ж відбиття у щодо гіперплощини ортогональної до ${\displaystyle \alpha }$просто розвертає порядок у цій послідовності. Зокрема якщо ${\displaystyle \lambda }$є старшою вагою, то для всіх ${\displaystyle \alpha }$ число r є рівним нулю.

Для незвідного скінченновимірного представлення із старшою вагою ${\displaystyle \lambda }$цілочисловий елемент ${\displaystyle \alpha }$ є вагою тоді і тільки тоді, коли він і всі його спряжені щодо дії групи Вейля елементи є нижчими, ніж ${\displaystyle \lambda }$.

Для розмірності незвідного скінченновимірного представлення ${\displaystyle V_{\lambda }}$ із старшою вагою ${\displaystyle \lambda }$виконується формула Вейля

${\displaystyle \dim(V_{\lambda })={\prod _{\alpha \in R^{+}}(\lambda +\rho ,\alpha ) \over \prod _{\alpha \in R^{+}}(\rho ,\alpha )}}$

де ${\displaystyle \rho }$позначає суму додатних коренів поділену на 2.

Якщо ${\displaystyle \omega _{1},\ldots ,\omega _{n}}$є системою фундаментальних ваг, то ${\displaystyle V_{\omega _{i}}}$називаються фундаментальними незвідними модулями.

Значення фундаментальних незвідних модулів полягає у тому, що якщо вони відомі, то всі інші незвідні скінченновимірні модулі (що перебувають у взаємно однозначній відповідності із цілочисловими домінантними вагами) отримуються як підмодулі їх тензорних добутків. Зокрема якщо ${\displaystyle \lambda =m_{1}\omega _{1}+\ldots +m_{n}\omega _{n}}$то ${\displaystyle V_{\lambda }}$ є підмодулем тензорного добутку ${\displaystyle \bigotimes _{i=1}^{n}V_{\omega _{i}}^{m_{i}}}$, де ${\displaystyle V_{\omega _{i}}^{m_{i}}}$позначає тензорний степінь.

Модулі ${\displaystyle V_{\omega _{1}}}$, що відповідають фундаментальним вагам ${\displaystyle \omega _{1}}$ називаються базовими фундаментальними. Більшість інших фундаментальних модулів можна отримати як зовнішні добутки базових фундаментальних модулів.

Зокрема для класичних алгебр типу A_n розмірність базових фундаментальних модулів є рівною n+1, а всі інші фундаментальні модулі отримуються як ${\displaystyle V_{\omega _{i}}=\wedge ^{i}V_{\omega _{1}}}$ і відповідно для розмірностей цих модулів виконується рівність ${\displaystyle \dim V_{\omega _{i}}=C_{n+1}^{i},}$ де ${\displaystyle C_{n+1}^{i}}$позначає біноміальний коефіцієнт.

Для класичних алгебр типу B_n розмірність базових фундаментальних модулів є рівною 2n+1, фундаментальні модулі для фундаментальних ваг ${\displaystyle \omega _{1},\ldots ,\omega _{n-1}}$ отримуються як ${\displaystyle V_{\omega _{i}}=\wedge ^{i}V_{\omega _{1}}}$ і відповідно для розмірностей цих модулів виконується рівність ${\displaystyle \dim V_{\omega _{i}}=C_{2n+1}^{i}.}$ Фундаментальний модуль для фундаментальної ваги ${\displaystyle \omega _{n}}$для алгебри B_n має розмірність 2ⁿ і його можна отримати із алгебри Кліффорда простору ${\displaystyle V_{\omega _{1}}}$.

Для класичних алгебр типу D_n розмірність базових фундаментальних модулів є рівною 2n, фундаментальні модулі для фундаментальних ваг ${\displaystyle \omega _{1},\ldots ,\omega _{n-2}}$ отримуються як ${\displaystyle V_{\omega _{i}}=\wedge ^{i}V_{\omega _{1}}}$ і відповідно для розмірностей цих модулів виконується рівність ${\displaystyle \dim V_{\omega _{i}}=C_{2n}^{i}.}$Фундаментальні модулі для фундаментальних ваг ${\displaystyle \omega _{n-1},\omega _{n}}$для алгебри D_n обидва мають розмірність 2ⁿ і їх можна отримати із алгебри Кліффорда простору ${\displaystyle V_{\omega _{1}}}$.

Для класичних алгебр типу C_n розмірність базових фундаментальних модулів є рівною 2n, фундаментальні модулі для інших фундаментальних ваг отримуються як ядра деяких лінійних відображень із ${\displaystyle \wedge ^{i}V_{\omega _{1}}}$у ${\displaystyle \wedge ^{i-2}V_{\omega _{1}}}$і для розмірностей цих модулів виконується рівність ${\displaystyle \dim V_{\omega _{i}}=C_{2n}^{i}-C_{2n}^{i-2}.}$