Досконале число

У теорії чисел досконале число — натуральне число, що дорівнює сумі його додатних дільників, не враховуючи самого числа. Наприклад, 6 має дільники 1, 2, 3 (не враховуючи його самого), $6=1+2+3$ , тому 6 — досконале число.

Ілюстрація досконалого числа 6

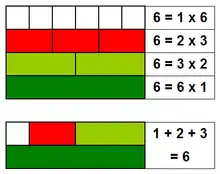
Сума дільників числа, не враховуючи самого числа, називається аліквотною сумою, тому досконале число — це число, що дорівнює його аліквотній сумі. Що рівносильно, що досконале число — число, яке є половиною суми всіх своїх додатних дільників, враховуючи себе. У символьному записі: $\sigma _{1}(n)=2n$ , де $\sigma _{1}(n)$ — функція суми дільників числа $n$ . Наприклад, 28 — досконале, оскільки $1+2+4+7+14+28=56=2\cdot 28$ .

Це стародавнє означення, воно з'явилось ще в Началах Евкліда (VII.22), де такі числа називалися досконалими, ідеальними чи повними. Евклід також довів правило утворення (IX/36), за яким ${\frac {q(q+1)}{2}}$ є парним досконалим числом тоді, коли $q=2^{p}-1$ , $q$ і $p$ — прості числа. Такі $q$ називаються простими числами Мерсенна. Через два тисячоліття Ейлер довів, що всі парні досконалі числа мають таку форму[1]. Цей результат відомий як теорема Евкліда-Ейлера.

Невідомо, чи існують непарні досконалі числа і чи є нескінченною послідовність досконалих чисел. Декілька перших досконалих чисел — 6, 28, 496, 8128 (див. послідовність послідовність A000396 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.

Історія

Приблизно в 300-му році до н. е. Евклід показав, що, якщо $2^{p}-1$ — просте число, то $2^{p-1}(2^{p}-1)$ — досконале число. Перші 3 досконалі числа були єдиними, які знала давньогрецька математика і число 8128, яке знайшов Нікомах приблизно у 100-му році н. е.[2] Нікомах стверджував без доведення, що будь-яке досконале число має вигляд $2^{n-1}(2^{n}-1)$ , де $2^{n}-1$ — просте число.[3][4] Здається, він не знав, що $n$ також має бути простим числом. Також він помилково вважав, що досконалі числа по черзі закінчуються на 6 і на 8 (перші п'ять досконалих чисел закінчуються на 6, 8, 6, 8, 6 відповідно, але шосте закінчується знову на 6). Філон Олександрійський у своїй книзі першого століття «Про створення світу» згадує досконалі числа, стверджуючи, що світ був створений за 6 днів, а Місяць здійснює повний оберт по орбіті за 28 днів, тому що 6 і 28 — досконалі. До Філона приєднались Оріген[5] і Дідим Сліпець, котрі зазначають, що є лише чотири досконалі числа, менші за 10000 (коментар до книги Буття 1.14-19).[6] Св. Августин на початку п'ятого віку н. е. зазначає досконалі числа у книзі «Місто Боже» (книга XI, глава 30), повторюючи висловлювання, що Бог створив світ за 6 днів, бо 6 — найменше досконале число. Єгипетський математик Ізмаїл ібн Фоллус (1194-1252) згадує наступні три досканалі числа (33,550,336; 8,589,869,056; 137,438,691,328) і ще декілька, які виявились хибними.[7] Перша згадка п'ятого досконалого числа європейцями — рукопис, написаний між 1456 і 1461 роками невідомим математиком.[8] У 1588 році італійський математик П'єтро Катальді знайшов шосте (8,589,869,056) і сьоме (137,438,691,328) досконалі числа, а також довів, що кожне досконале число, отримане з правила Евкліда, закінчується на 6 чи 8.[9][10][11]

Парні досконалі числа

Див. також: Теорема Евкліда-Ейлера.

Евклід довів, що $2^{p-1}(2^{p}-1)$ є досконалими, коли $2^{p}-1$ є простим (Начала, твердження IX.36).

Наприклад, перші чотири досконалі числа, отримані за допомогою цієї формули:

при

p=2

:

2^{1}(2^{2}-1)=2\cdot 3=6,

при

p=3

:

2^{2}(2^{3}-1)=4\cdot 7=28,

при

p=5

:

2^{4}(2^{5}-1)=16\cdot 31=496,

при

p=7

:

2^{6}(2^{7}-1)=64\cdot 127=8128.

Прості числа вигляду $2^{p}-1$ , відомі як прості числа Мерсенна, названі на честь монаха сімнадцятого століття Марена Мерсенна, що вивчав теорію чисел і досконалі числа. Для того, щоб $2^{p}-1$ було простим, необхідно щоб і $p$ було простим. Але це не достатня умова; наприклад, $2^{11}-1=2047=23\times 89$ не є простим[12].Насправді, прості числа Мерсенна дуже рідкісні — з 2,610,944 простих чисел менших 43112609[13], число $(2^{p}-1)$ є простим лише для 47 з них.

Хоча Нікомах стверджував (без доведення), що всі досконалі числа мають вигляд $2^{n-1}(2^{n}-1)$ , де $2^{n}-1$ — просте число (саме твердження було трохи в іншій формі), Ібн аль-Хайсам приблизно в 1000-му році н. е. припускав, що формула описує лише будь-яке парне досконале число[14]. Тільки в XVIII столітті Леонард Ейлер довів, що формула $2^{p-1}(2^{p}-1)$ описує всі парні досконалі числа. Таким чином існує взаємно однозначна відповідність між парними досконалими числами і простими числами Мерсенна; кожне просте число Мерсенна породжує одне парне досконале число, і навпаки. Цей результат часто називають теоремою Евкліда-Ейлера.

Вичерпний пошук у рамках проекту GIMPS показав, що першим 47-ми парним досконалим числам вигляду $2^{p-1}(2^{p}-1)$ відповідають[15]

p

= 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801 і 43112609 послідовність A000043 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.[16]

Також знайдено чотири більші досконалі числа, а саме при $p$ =57,885,161; 74,207,281; 77,232,917 і 82,589,933, але в цих межах можуть бути і інші. Станом на грудень 2018 року відомо 51 просте число Мерсенна[17] і, відповідно, 51 парне досконале число (найбільше з яких — $2^{82589932}(2^{82589933}-1)$ з 49,724,095 цифрами). Невідомо чи існує нескінченно багато досконалих чисел і простих чисел Мерсенна.

Крім того, що будь-яке парне досконале число має вигляд $2^{p-1}(2^{p}-1)$ , воно ще є $(2^{p}-1)$ -им трикутним числом (і, як наслідок, є сумою цілих чисел від 1 до $2^{p}-1$ ), а також є $(2^{p-1})$ -им шестикутним числом. Більш того, будь-яке парне досконале число (за винятком 6) є $\left({\frac {2^{p}-1}{3}}\right)$ -им центрованим дев'ятикутним числом, а значить воно дорівнює сумі $2^{\frac {p-1}{2}}$ перших непарних кубів:

{\begin{aligned}6=2^{1}\left(2^{2}-1\right)&=1+2+3,\\[8pt]28=2^{2}\left(2^{3}-1\right)&=1+2+3+4+5+6+7=1^{3}+3^{3},\\[8pt]496=2^{4}\left(2^{5}-1\right)&=1+2+3+\cdots +29+30+31\\&=1^{3}+3^{3}+5^{3}+7^{3},\\[8pt]8128=2^{6}\left(2^{7}-1\right)&=1+2+3+\cdots +125+126+127\\&=1^{3}+3^{3}+5^{3}+7^{3}+9^{3}+11^{3}+13^{3}+15^{3},\\[8pt]33550336=2^{12}\left(2^{13}-1\right)&=1+2+3+\cdots +8189+8190+8191\\&=1^{3}+3^{3}+5^{3}+\cdots +123^{3}+125^{3}+127^{3}.\end{aligned}}

Парні досконалі числа (крім 6) мають вигляд

T_{2^{p}-1}=1+{\frac {(2^{p}-2)\times (2^{p}+1)}{2}}=1+9\times T_{\frac {2^{p}-2}{3}}

,

де кожне трикутне число $T_{7}=28$ , $T_{31}=496$ , $T_{127}=8128$ після віднімання одиниці і ділення на дев'ять закінчується на 3 або 5; послідовність починається з $T_{2}=3$ , $T_{10}=55$ , $T_{42}=903$ , $T_{2730}=3727815,\dots$ [18] Це можна переформулювати наступним чином: сумування цифр будь-якого парного досконалого числа (крім 6), а потім повтор таких дій з отриманими результатами до моменту, коли залишиться одна цифра (знаходження цифрового кореня), дасть в результаті одиницю. Наприклад, цифровий корінь числа 8128 дорівнює одиниці, бо $8+1+2+8=19$ , $1+9=10$ , $1+0=1$ . Це справедливо для усіх чисел вигляду $2^{m-1}(2^{m}-1)$ , де $m$ — непарне число.

Завдяки своїй формі $2^{p-1}(2^{p}-1)$ кожне парне досконале число записується у двійковій системі як $p$ одиниць, а за ними $(p-1)$ нулів. Наприклад,

6_{10}=2^{2}+2^{1}=110_{2},

28_{10}=2^{4}+2^{3}+2^{2}=11100_{2},

496_{10}=2^{8}+2^{7}+2^{6}+2^{5}+2^{4}=111110000_{2},

8128_{10}=2^{12}+2^{11}+\cdots +2^{7}+2^{6}=1111111000000_{2}.

Таким чином парні досконалі числа є згубними числами.

Кожне парне досконале число також є практичним числом.

Непарні досконалі числа

Невідомо чи існує хоч якесь непарне досконале число, хоча деякі результати у цьому напрямі були отримані. У 1496 році Жак Лефевр стверджував, що правило Евкліда дає абсолютно всі досконалі числа[19], з чого слідує відсутність непарних досконалих чисел. Ейлер стверджував, що найважчим питанням є питання існування непарних досконалих чисел[20]. Нещодавно Карл Померанс представив евристичний аргумент, який передбачає, що дійсно непарного досконалого числа не має існувати[21]. Усі досконалі числа також є гармонічними числами Оре, а також існує гіпотеза, що немає непарних гармонічних чисел Оре (крім одиниці).

Будь-яке непарне досконале число $N$ має задовольняти наступним умовам:

$N\geq 10^{1500}$ [22]
$N$ не ділиться на 105[23]
$N$ конгурентне або 1 по модулю 12, або 117 по модулю 468, або 81 по модулю 324[24]
$N$ має вигляд $N=q^{\alpha }p_{1}^{2e_{1}}\cdots p_{k}^{2e_{k}}$ , де

$q,p_{1},\dots ,p_{k}$ є різними простими числами (Ейлер);
$N\equiv \alpha \equiv 1$ (mod 4) (Ейлер);
Найменший простий дільник числа $N$ менший за ${\frac {2k+8}{3}}$ ;[25]
Або $q^{\alpha }>10^{62}$ , або $p_{j}^{2e_{j}}>10^{62}$ для деякого $j$ ;[22]
$N<2^{(4^{k+1}-2^{k+1})}$ ;[26][27]
$\alpha +2e_{1}+2e_{2}+\dots +2e_{k}\geq {\frac {21k-18}{8}}$ ;[28][29]
$qp_{1}p_{2}\dots p_{k}<2N^{\frac {17}{26}}$ .[30]

Найбільший простий дільник числа $N$ більший за $10^{8}$ [31] і менший за $(3N)^{\frac {1}{3}}$ .[32]
Наступний найбільший простий дільник $N$ більший за $10^{4}$ і менший за $(2N)^{\frac {1}{5}}$ .[33][34]
Третій найбільший простий дільник $N$ більший за 100.[35]
$N$ має щонайменше 101 простий дільник, де щонайменше 10 різних.[36]
Якщо $N$ не ділиться на 3, то $N$ має щонайменше 12 простих дільників.[37]

Також відомо декілька другорядних результатів, що стосуються показників $e_{1},\dots ,e_{k}$ числа $N=q^{\alpha }p_{1}^{2e_{1}}\cdots p_{k}^{2e_{k}}$ .

Не всі $e_{i}\equiv 1$ (mod 3).[38]
Не всі $e_{i}\equiv 2$ (mod 5).[39]
Якщо $e_{i}\equiv 1$ (mod 3) або $e_{i}\equiv 2$ (mod 5), найменший простий дільник числа $N$ буде знаходитись в межах від $10^{8}$ до $10^{1000}$ .
У загальному випадку, якщо всі $2e_{i}+1$ мають простий дільник у скінченній множині $S$ , то найменший простий дільник числа $N$ має бути найменшим за ефективно обчислювальну константу, що залежить лише від $S$ .
Якщо $(e_{i},\dots ,e_{k})=(1,\dots ,1,2,\dots ,2)$ з $t$ одиницями і $u$ двійками, то ${\frac {t-1}{4}}\leq u\leq 2t+{\sqrt {\alpha }}$ .[40]
$(e_{i},\dots ,e_{k})\neq (1,\dots ,1,3)$ ,[41] $(1,\dots ,1,5)$ , $(1,\dots ,1,6)$ .[42]
Якщо $e_{1}=\dots =e_{k}=e$ , то

$e$ не може дорівнювати 3,[43] 5, 24,[44] 6, 8, 11, 14 або 18.[42]
$k\leq 2e^{2}+8e+2$ і $N<2^{4^{2e^{2}+8e+3}}$ .[45]

У 1888 році Сильвестр стверджував: «… довгі роздуми на цю тему переконали мене, що існування будь-якого такого (непарного досконалого) числа — це вихід із величезної павутини умов, що його оточують, і є просто чудом.»[46]

Багато властивостей, доведених відносно непарних досконалих чисел, також стосуються чисел Декарта, а тому Пейс Нільсен припустив, що достатнє вивчення таких чисел може привести до доведення відсутності непарних досконалих чисел.[47]

Незначні результати

Усі парні досконалі числа мають дуже точну форму; непарні досконалі числа або не існують, або є дуже рідкісними. Є цілий ряд результатів щодо досконалих чисел, які насправді досить легко довести, але, втім, є вражаючими; деякі з них підходять під сильний закон малих чисел Річарда Ґая:

28 — єдине парне досконале число вигляду $x^{3}+1$ [48]
28 — також єдине парне досконале число, яке є сумою кубів двох додатних чисел[49]
Сума чисел, обернених до дільників досконалого числа, дорівнює двійці (щоб отримати це, необхідно скористатися означенням досконалого числа $\sigma _{1}(n)=2n$ і поділити обидві частини рівності на $n$ ):

Для 6 маємо: ${\frac {1}{6}}+{\frac {1}{3}}+{\frac {1}{2}}+{\frac {1}{1}}=2$ ;
Для 28 маємо: ${\frac {1}{28}}+{\frac {1}{14}}+{\frac {1}{7}}+{\frac {1}{4}}+{\frac {1}{2}}+{\frac {1}{1}}=2$ , і так далі.

Кількість дільників будь-якого досконалого числа (парного чи непарного) має бути парною, оскільки досконале число $N$ не може бути повним квадратом[50]

З двох зазначених вище властивостей випливає, що кожне досконале число є гармонічним числом Оре.

Парні досконалі числа не є трапецієвидними числами; тобто їх не можна представити у вигляді різниці двох додатних непослідовних трикутних чисел. Існує лише три типи нетрапецієвидних чисел: парні досконалі числа, степені двійки і числа вигляду $2^{n-1}(2^{n}-1)$ , які утворені як добуток простого числа Ферма $2^{n}-1$ та $2^{n-1}$ , що аналогічно побудові досконалих чисел з простих чисел Мерсенна.[51]
Кількість досконалих чисел менших за $n$ менша за $c{\sqrt {n}}$ , де $c$ — додатна константа.[52] Насправді це $o({\sqrt {n}})$ (використовується позначення $o$ -малого).[53]
Кожне парне досконале число закінчується на 6 чи 28 в десятковій системі і закінчується на 1 (за винятком числа 6) в системі за базою 9[54][55]. Тому цифровий корінь будь-якого парного досконалого числа (відмінного від 6) дорівнює 1.
6 — єдине досконале число, яке є безквадратичним.[56]

Пов'язані поняття

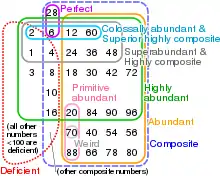
Діаграма Ейлера для надлишкових, недостатніх, досконалих і т. д. чисел, менших за 100.

Сума власних дільників дає різні інші види чисел. Числа, де сума їх дільників менша за саме число, називають недостатніми, а де більша — надлишковими. Ці терміни і саме поняття досконалих чисел прийшло до нас з грецької нумерології. Пари чисел, які є сумами власних дільників один одного, називаються дружними, а більші цикли таких чисел називаються компанійськими. Натуральне число таке, що кожне менше за нього натуральне число є сумою його різних дільників, називається практичним.

За означенням, досконале число — нерухома точка обмеженої функції дільників $s(n)=\sigma (n)-n$ , а пов'язана з досконалими числами аліквотна послідовність є постійною послідовністю. Всі досконалі числа також є ${\mathcal {S}}$ -досконалими або числами Гранвіля.

Напівдосконале число — натуральне число, яке дорівнює сумі всіх або деяких власних дільників. Напівдосконале число, яке дорівнює сумі всіх власних дільників є досконалим числом. Більшість надлишкових чисел також є напівдосконалими; надлишкові числа, що не є напівдосконалими, називаються дивними.

Див. також

Гіпердосконале число
Група Ленстера
Список досконалих чисел
Багаторазове досконале число
Супердосконалі числа

Примітки

Caldwell, Chris, «A proof that all even perfect numbers are a power of two times a Mersenne prime»
Dickson, L. E. (1919). History of the Theory of Numbers, Vol.~I. Washington: Carnegie Institution of Washington. p.~4.
«Perfect numbers». www-groups.dcs.st-and.ac.uk. Retrieved 9 May 2018
У «Вступі в арифметику» (глава 16) він стверджує, що є акуратний і безвідмовний метод, який описує кожне досконале число і не описує жодне інше, що здійснюється вказаним ним чином, який є еквівалентним знаходженню трикутних чисел за допомогою простих чисел Мерсенна
Commentary on the Gospel of John 28.1.1-4, with further references in the Sources Chrétiennes edition: vol.~385, 58-61
http://torreys.org/sblpapers2015/S22-05\_philonic\_arithmological\_exegesis.pdf
Roshdi Rashed, The Development of Arabic Mathematics: Between Arithmetic and Algebra (Dordrecht: Kluwer Academic Publishers, 1994), pp. 328—329.
Bayerische Staatsbibliothek, Clm 14908. See David Eugene Smith (1925). History of Mathematics: Volume II. New York: Dover. p. 21. ISBN 0-486-20430-8.
Dickson, L. E. (1919). History of the Theory of Numbers, Vol. I. Washington: Carnegie Institution of Washington. p. 10
Pickover, C (2001). Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford: Oxford University Press. p. 360. ISBN 0-19-515799-0
Peterson, I (2002). Mathematical Treks: From Surreal Numbers to Magic Circles. Washington: Mathematical Association of America. p. 132. ISBN 88-8358-537-2
Усі дільники числа $2^{p}-1$ конгруентні одиниці по модулю $2p$ . Наприклад, $2^{11}-1=2047=23\times 89$ . І 23, і 89 дають остачу 1 при діленні на 22. Більш того, якщо $p$ є простим числом Софі Жермен (якщо $2p+1$ — теж просте і $2p+1$ конгруентне 1 або 7 за модулем 8), то $2p+1$ буде дільником числа $2^{p}-1$ , що справедливо для $p=11,23,83,131,179,191,239,251,\dots$ , (послідовність A002515 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)
«Numbers of prime $\leq 43112609$ ». Wolfram Alpha. Retrieved 2018-10-28
O'Connor, John J.;Robertson, Edmund F., «Abu Ali al-Hasan ibn al-Haytham», MacTutor History of Mathematics archive, University of St Andrews
GIMPS Milestones Report. Retrieved 2018-02-27
GIMPS Milestones Report. Retrieved 2018-02-27
«GIMPS Home». Mersenne.org. Retrieved 2018-12-21
Weisstein, Eric W. «Perfect Number». MathWorld
Dickson, L. E. (1919). History of the Theory of Numbers, Vol. I. Washington: Carnegie Institution of Washington. p. 6.
http://www.math.harvard.edu/~knill/seminars/perfect/handout.pdf
Oddperfect.org. Archived 2006-12-29 at the Wayback Machine
Ochem, Pascal; Rao, Michaël (2012). «Odd perfect numbers are greater than 101500» (PDF). Mathematics of Computation. 81 (279): 1869—1877. doi:10.1090/S0025-5718-2012-02563-4. ISSN 0025-5718. Zbl 1263.11005
Kühnel, Ullrich (1950). ``Verschärfung der notwendigen Bedingungen für die Existenz von ungeraden vollkommenen Zahlen. Mathematische Zeitschrift (in German). 52: 202—211. doi:10.1007/BF02230691
Roberts, T (2008). «On the Form of an Odd Perfect Number» (PDF). Australian Mathematical Gazette. 35 (4): 244.
Grün, O (1952). «Über ungerade vollkommene Zahlen». Mathematische Zeitschrift. 55 (3): 353—354. doi:10.1007/BF01181133
Chen, Yong-Gao; Tang, Cui-E (2014). «Improved upper bounds for odd multiperfect numbers». Bulletin of the Australian Mathematical Society. 89 (3): 353—359
Nielsen, Pace P. (2003). «An upper bound for odd perfect numbers». Integers. 3: A14–A22. Retrieved 23 March 2021
Zelinsky, Joshua (25 May 2018). «An improvement of an inequality of Ochem and Rao concerning odd perfect numbers». Integers. 18. arXiv:1706.07009. Bibcode:2017arXiv170607009Z. Retrieved 23 May 2018
Ochem, Pascal; Rao, Michaël (2014). «On the number of prime factors of an odd perfect number». Mathematics of Computation. 83 (289): 2435—2439. doi:10.1090/S0025-5718-2013-02776-7
Pomerance, Carl; Luca, Florian (2010). «On the radical of a perfect number». New York Journal of Mathematics. 16: 23–30. Retrieved 7 December 2018
Goto, T; Ohno, Y (2008). «Odd perfect numbers have a prime factor exceeding 108»(PDF). Mathematics of Computation. 77 (263): 1859—1868. Bibcode:2008MaCom..77.1859G.doi:10.1090/S0025-5718-08-02050-9. Retrieved 30 March 2011
Konyagin, Sergei; Acquaah, Peter (2012). «On Prime Factors of Odd Perfect Numbers». International Journal of Number Theory. 8 (6): 1537—1540. doi:10.1142/S1793042112500935
Zelinsky, Joshua (July 2019). «Upper bounds on the second largest prime factor of an odd perfect number». International Journal of Number Theory. 15 (6): 1183—1189. arXiv:1810.11734. doi:10.1142/S1793042119500659
Iannucci, DE (1999). «The second largest prime divisor of an odd perfect number exceeds ten thousand»(PDF). Mathematics of Computation. 68 (228): 1749—1760. Bibcode:1999MaCom..68.1749I. doi:10.1090/S0025-5718-99-01126-6. Retrieved 30 March 2011.
Iannucci, DE (2000). «The third largest prime divisor of an odd perfect number exceeds one hundred»(PDF). Mathematics of Computation. 69 (230): 867—879. Bibcode:2000MaCom..69..867I. doi:10.1090/S0025-5718-99-01127-8. Retrieved 30 March 2011.
Nielsen, Pace P. (2015). «Odd perfect numbers, Diophantine equations, and upper bounds»(PDF). Mathematics of Computation. 84 (295): 2549—2567. doi:10.1090/S0025-5718-2015-02941-X. Retrieved 13 August 2015.
Nielsen, Pace P. (2007). «Odd perfect numbers have at least nine distinct prime factors»(PDF). Mathematics of Computation. 76 (260): 2109—2126. arXiv: math/0602485. Bibcode:2007MaCom..76.2109N. doi:10.1090/S0025-5718-07-01990-4. Retrieved 30 March 2011.
McDaniel, Wayne L. (1970). «The non-existence of odd perfect numbers of a certain form». Archiv der Mathematik. 21 (1): 52–53. doi:10.1007/BF01220877. ISSN 1420-8938. MR 0258723
Fletcher, S. Adam; Nielsen, Pace P.; Ochem, Pascal (2012). «Sieve methods for odd perfect numbers»(PDF). Mathematics of Computation. 81 (279): 1753?1776. doi:10.1090/S0025-5718-2011-02576-7. ISSN 0025-5718. MR 2904601
Cohen, G. L. (1987). «On the largest component of an odd perfect number». Journal of the Australian Mathematical Society, Series A. 42 (2): 280—286. doi:10.1017/S1446788700028251. ISSN 1446-8107. MR 0869751
Kanold, Hans-Joachim (1950). «Satze uber Kreisteilungspolynome und ihre Anwendungen auf einige zahlentheoretisehe Probleme. II». Journal für die reine und angewandte Mathematik. 188 (1): 129—146. doi:10.1515/crll.1950.188.129. ISSN 1435-5345. MR 0044579
Cohen, G. L.; Williams, R. J. (1985). «Extensions of some results concerning odd perfect numbers» (PDF). Fibonacci Quarterly. 23 (1): 70–76. ISSN 0015-0517. MR 0786364
Hagis, Peter Jr.; McDaniel, Wayne L. (1972). «A new result concerning the structure of odd perfect numbers». Proceedings of the American Mathematical Society. 32 (1): 13–15. doi:10.1090/S0002-9939-1972-0292740-5. ISSN 1088-6826. MR 0292740
McDaniel, Wayne L.; Hagis, Peter Jr. (1975). «Some results concerning the non-existence of odd perfect numbers of the form $p^{\alpha }M^{2\beta }$ »(PDF). Fibonacci Quarterly. 13 (1): 25–28. ISSN 0015-0517. MR 0354538
Yamada, Tomohiro (2019). «A new upper bound for odd perfect numbers of a special form». Colloquium Mathematicum. 156 (1): 15–21. arXiv:1706.09341. doi:10.4064/cm7339-3-2018. ISSN 1730-6302
The Collected Mathematical Papers of James Joseph Sylvester p. 590, tr. from «Sur les nombres dits de Hamilton», Compte Rendu de l'Association Française (Toulouse, 1887), pp. 164—168.
Nadis, Steve (10 September 2020). «Mathematicians Open a New Front on an Ancient Number Problem». Quanta Magazine. Retrieved 10 September 2020.
Makowski, A. (1962). «Remark on perfect numbers». Elem. Math. 17 (5): 109.
Gallardo, Luis H. (2010). «On a remark of Makowski about perfect numbers». Elem. Math. 65: 121—126. doi:10.4171/EM/149
Yan, Song Y. (2012), Computational Number Theory and Modern Cryptography, John Wiley, Sons, Section 2.3, Exercise 2(6), ISBN 9781118188613.
Jones, Chris; Lord, Nick (1999). «Characterising non-trapezoidal numbers». The Mathematical Gazette. The Mathematical Association. 83 (497): 262—263. doi:10.2307/3619053. JSTOR 3619053
Hornfeck, B (1955). «Zur Dichte der Menge der vollkommenen zahlen». Arch. Math. 6 (6): 442—443. doi:10.1007/BF01901120
Kanold, HJ (1956). «Eine Bemerkung uber die Menge der vollkommenen zahlen». Math. Ann. 131 (4): 390—392. doi:10.1007/BF01350108
H. Novarese. Note sur les nombres parfaits Texeira J. VIII (1886), 11–16.
Dickson, L. E. (1919). History of the Theory of Numbers, Vol. I. Washington: Carnegie Institution of Washington. p. 25.
Redmond, Don (1996). Number Theory: An Introduction to Pure and Applied Mathematics. Chapman, Hall/CRC Pure and Applied Mathematics. 201. CRC Press. Problem 7.4.11, p. 428. ISBN 9780824796969.

Посилання

David Moews: Perfect, amicable and sociable numbers
Perfect numbers — History and Theory
Weisstein, Eric W. Perfect Number(англ.) на сайті Wolfram MathWorld.
OddPerfect.org A projected distributed computing project to search for odd perfect numbers.
Great Internet Mersenne Prime Search (GIMPS)
Perfect Numbers, math forum at Drexel.
Grimes, James. 8128: Perfect Numbers. Numberphile. Архів оригіналу за 31 травня 2013. Процитовано 2 квітня 2013.

Література

Euclid, Elements, Book IX, Proposition 36. See D.E. Joyce's website for a translation and discussion of this proposition and its proof.
Kanold, H.-J. (1941). Untersuchungen über ungerade vollkommene Zahlen. Journal für die Reine und Angewandte Mathematik 183: 98–109.
Steuerwald, R. Verschärfung einer notwendigen Bedingung für die Existenz einer ungeraden vollkommenen Zahl. S.-B. Bayer. Akad. Wiss. 1937: 69–72.

Додаткова література

Nankar, M.L.: "History of perfect numbers, " Ganita Bharati 1, no. 1–2 (1979), 7–8.
Riele, H.J.J. «Perfect Numbers and Aliquot Sequences» in H.W. Lenstra and R. Tijdeman (eds.): Computational Methods in Number Theory, Vol. 154, Amsterdam, 1982, pp. 141–157.
Riesel, H. Prime Numbers and Computer Methods for Factorisation, Birkhauser, 1985.
Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. с. 15–98. ISBN 1-4020-2546-7. Zbl 1079.11001.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Caldwell, Chris, «A proof that all even perfect numbers are a power of two times a Mersenne prime»

[2] Dickson, L. E. (1919). History of the Theory of Numbers, Vol.~I. Washington: Carnegie Institution of Washington. p.~4.

[3] «Perfect numbers». www-groups.dcs.st-and.ac.uk. Retrieved 9 May 2018

[4] У «Вступі в арифметику» (глава 16) він стверджує, що є акуратний і безвідмовний метод, який описує кожне досконале число і не описує жодне інше, що здійснюється вказаним ним чином, який є еквівалентним знаходженню трикутних чисел за допомогою простих чисел Мерсенна

[5] Commentary on the Gospel of John 28.1.1-4, with further references in the Sources Chrétiennes edition: vol.~385, 58-61

[6] ttp://torreys.org/sblpapers2015/S22-05\_philonic\_arithmological\_exegesis.pdf

[7] Roshdi Rashed, The Development of Arabic Mathematics: Between Arithmetic and Algebra (Dordrecht: Kluwer Academic Publishers, 1994), pp. 328—329.

[8] Bayerische Staatsbibliothek, Clm 14908. See David Eugene Smith (1925). History of Mathematics: Volume II. New York: Dover. p. 21. ISBN 0-486-20430-8.

[9] Dickson, L. E. (1919). History of the Theory of Numbers, Vol. I. Washington: Carnegie Institution of Washington. p. 10

[10] Pickover, C (2001). Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford: Oxford University Press. p. 360. ISBN 0-19-515799-0

[11] Peterson, I (2002). Mathematical Treks: From Surreal Numbers to Magic Circles. Washington: Mathematical Association of America. p. 132. ISBN 88-8358-537-2

[12] Усі дільники числа $2^{p}-1$ конгруентні одиниці по модулю $2p$ . Наприклад, $2^{11}-1=2047=23\times 89$ . І 23, і 89 дають остачу 1 при діленні на 22. Більш того, якщо $p$ є простим числом Софі Жермен (якщо $2p+1$ — теж просте і $2p+1$ конгруентне 1 або 7 за модулем 8), то $2p+1$ буде дільником числа $2^{p}-1$ , що справедливо для $p=11,23,83,131,179,191,239,251,\dots$ , (послідовність A002515 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

[13] «Numbers of prime $\leq 43112609$ ». Wolfram Alpha. Retrieved 2018-10-28

[14] O'Connor, John J.;Robertson, Edmund F., «Abu Ali al-Hasan ibn al-Haytham», MacTutor History of Mathematics archive, University of St Andrews

[15] GIMPS Milestones Report. Retrieved 2018-02-27

[16] GIMPS Milestones Report. Retrieved 2018-02-27

[17] «GIMPS Home». Mersenne.org. Retrieved 2018-12-21

[18] Weisstein, Eric W. «Perfect Number». MathWorld

[19] Dickson, L. E. (1919). History of the Theory of Numbers, Vol. I. Washington: Carnegie Institution of Washington. p. 6.

[20] ttp://www.math.harvard.edu/~knill/seminars/perfect/handout.pdf

[21] Oddperfect.org. Archived 2006-12-29 at the Wayback Machine

[:0-22] Ochem, Pascal; Rao, Michaël (2012). «Odd perfect numbers are greater than 101500» (PDF). Mathematics of Computation. 81 (279): 1869—1877. doi:10.1090/S0025-5718-2012-02563-4. ISSN 0025-5718. Zbl 1263.11005

[23] Kühnel, Ullrich (1950). ``Verschärfung der notwendigen Bedingungen für die Existenz von ungeraden vollkommenen Zahlen. Mathematische Zeitschrift (in German). 52: 202—211. doi:10.1007/BF02230691

[24] Roberts, T (2008). «On the Form of an Odd Perfect Number» (PDF). Australian Mathematical Gazette. 35 (4): 244.

[25] Grün, O (1952). «Über ungerade vollkommene Zahlen». Mathematische Zeitschrift. 55 (3): 353—354. doi:10.1007/BF01181133

[26] Chen, Yong-Gao; Tang, Cui-E (2014). «Improved upper bounds for odd multiperfect numbers». Bulletin of the Australian Mathematical Society. 89 (3): 353—359

[27] Nielsen, Pace P. (2003). «An upper bound for odd perfect numbers». Integers. 3: A14–A22. Retrieved 23 March 2021

[28] Zelinsky, Joshua (25 May 2018). «An improvement of an inequality of Ochem and Rao concerning odd perfect numbers». Integers. 18. arXiv:1706.07009. Bibcode:2017arXiv170607009Z. Retrieved 23 May 2018

[29] Ochem, Pascal; Rao, Michaël (2014). «On the number of prime factors of an odd perfect number». Mathematics of Computation. 83 (289): 2435—2439. doi:10.1090/S0025-5718-2013-02776-7

[30] Pomerance, Carl; Luca, Florian (2010). «On the radical of a perfect number». New York Journal of Mathematics. 16: 23–30. Retrieved 7 December 2018

[31] Goto, T; Ohno, Y (2008). «Odd perfect numbers have a prime factor exceeding 108»(PDF). Mathematics of Computation. 77 (263): 1859—1868. Bibcode:2008MaCom..77.1859G.doi:10.1090/S0025-5718-08-02050-9. Retrieved 30 March 2011

[32] Konyagin, Sergei; Acquaah, Peter (2012). «On Prime Factors of Odd Perfect Numbers». International Journal of Number Theory. 8 (6): 1537—1540. doi:10.1142/S1793042112500935

[33] Zelinsky, Joshua (July 2019). «Upper bounds on the second largest prime factor of an odd perfect number». International Journal of Number Theory. 15 (6): 1183—1189. arXiv:1810.11734. doi:10.1142/S1793042119500659

[34] Iannucci, DE (1999). «The second largest prime divisor of an odd perfect number exceeds ten thousand»(PDF). Mathematics of Computation. 68 (228): 1749—1760. Bibcode:1999MaCom..68.1749I. doi:10.1090/S0025-5718-99-01126-6. Retrieved 30 March 2011.

[35] Iannucci, DE (2000). «The third largest prime divisor of an odd perfect number exceeds one hundred»(PDF). Mathematics of Computation. 69 (230): 867—879. Bibcode:2000MaCom..69..867I. doi:10.1090/S0025-5718-99-01127-8. Retrieved 30 March 2011.

[36] Nielsen, Pace P. (2015). «Odd perfect numbers, Diophantine equations, and upper bounds»(PDF). Mathematics of Computation. 84 (295): 2549—2567. doi:10.1090/S0025-5718-2015-02941-X. Retrieved 13 August 2015.

[37] Nielsen, Pace P. (2007). «Odd perfect numbers have at least nine distinct prime factors»(PDF). Mathematics of Computation. 76 (260): 2109—2126. arXiv: math/0602485. Bibcode:2007MaCom..76.2109N. doi:10.1090/S0025-5718-07-01990-4. Retrieved 30 March 2011.

[38] McDaniel, Wayne L. (1970). «The non-existence of odd perfect numbers of a certain form». Archiv der Mathematik. 21 (1): 52–53. doi:10.1007/BF01220877. ISSN 1420-8938. MR 0258723

[39] Fletcher, S. Adam; Nielsen, Pace P.; Ochem, Pascal (2012). «Sieve methods for odd perfect numbers»(PDF). Mathematics of Computation. 81 (279): 1753?1776. doi:10.1090/S0025-5718-2011-02576-7. ISSN 0025-5718. MR 2904601

[40] Cohen, G. L. (1987). «On the largest component of an odd perfect number». Journal of the Australian Mathematical Society, Series A. 42 (2): 280—286. doi:10.1017/S1446788700028251. ISSN 1446-8107. MR 0869751

[41] Kanold, Hans-Joachim (1950). «Satze uber Kreisteilungspolynome und ihre Anwendungen auf einige zahlentheoretisehe Probleme. II». Journal für die reine und angewandte Mathematik. 188 (1): 129—146. doi:10.1515/crll.1950.188.129. ISSN 1435-5345. MR 0044579

[:1-42] Cohen, G. L.; Williams, R. J. (1985). «Extensions of some results concerning odd perfect numbers» (PDF). Fibonacci Quarterly. 23 (1): 70–76. ISSN 0015-0517. MR 0786364

[43] Hagis, Peter Jr.; McDaniel, Wayne L. (1972). «A new result concerning the structure of odd perfect numbers». Proceedings of the American Mathematical Society. 32 (1): 13–15. doi:10.1090/S0002-9939-1972-0292740-5. ISSN 1088-6826. MR 0292740

[44] McDaniel, Wayne L.; Hagis, Peter Jr. (1975). «Some results concerning the non-existence of odd perfect numbers of the form $p^{\alpha }M^{2\beta }$ »(PDF). Fibonacci Quarterly. 13 (1): 25–28. ISSN 0015-0517. MR 0354538

[45] Yamada, Tomohiro (2019). «A new upper bound for odd perfect numbers of a special form». Colloquium Mathematicum. 156 (1): 15–21. arXiv:1706.09341. doi:10.4064/cm7339-3-2018. ISSN 1730-6302

[46] The Collected Mathematical Papers of James Joseph Sylvester p. 590, tr. from «Sur les nombres dits de Hamilton», Compte Rendu de l'Association Française (Toulouse, 1887), pp. 164—168.

[47] Nadis, Steve (10 September 2020). «Mathematicians Open a New Front on an Ancient Number Problem». Quanta Magazine. Retrieved 10 September 2020.

[48] Makowski, A. (1962). «Remark on perfect numbers». Elem. Math. 17 (5): 109.

[49] Gallardo, Luis H. (2010). «On a remark of Makowski about perfect numbers». Elem. Math. 65: 121—126. doi:10.4171/EM/149

[50] Yan, Song Y. (2012), Computational Number Theory and Modern Cryptography, John Wiley, Sons, Section 2.3, Exercise 2(6), ISBN 9781118188613.

[51] Jones, Chris; Lord, Nick (1999). «Characterising non-trapezoidal numbers». The Mathematical Gazette. The Mathematical Association. 83 (497): 262—263. doi:10.2307/3619053. JSTOR 3619053

[52] Hornfeck, B (1955). «Zur Dichte der Menge der vollkommenen zahlen». Arch. Math. 6 (6): 442—443. doi:10.1007/BF01901120

[53] Kanold, HJ (1956). «Eine Bemerkung uber die Menge der vollkommenen zahlen». Math. Ann. 131 (4): 390—392. doi:10.1007/BF01350108

[54] H. Novarese. Note sur les nombres parfaits Texeira J. VIII (1886), 11–16.

[55] Dickson, L. E. (1919). History of the Theory of Numbers, Vol. I. Washington: Carnegie Institution of Washington. p. 25.

[56] Redmond, Don (1996). Number Theory: An Introduction to Pure and Applied Mathematics. Chapman, Hall/CRC Pure and Applied Mathematics. 201. CRC Press. Problem 7.4.11, p. 428. ISBN 9780824796969.