Поверхня Фермі

Рис.1. Поверхня Фермі вільних фермионів

Розглянемо ідеальний фермі-газ ${\displaystyle N}$ частинок. Згідно зі статистикою Фермі–Дірака, середнє число заповнення стану з енергією ${\displaystyle \epsilon _{i}}$ дається формулою[7]

${\displaystyle \langle n_{i}\rangle ={\frac {1}{e^{(\epsilon _{i}-\mu )/k_{\rm {B}}T}+1}},}$

де,

• ${\displaystyle \left\langle n_{i}\right\rangle }$ — середнє число заповнення ${\displaystyle i}$-го стану,
• ${\displaystyle \epsilon _{i}}$ — кінетична енергія ${\displaystyle i}$-го стану,
• ${\displaystyle \mu }$ — хімічний потенціал (при нульовій температурі це максимальна кінетична енергія, яку може мати частинка, тобто енергія Фермі ${\displaystyle E_{\rm {F}}}$),
• ${\displaystyle T}$ — абсолютна температура
• ${\displaystyle k_{\rm {B}}}$ — стала Больцмана.

У границі ${\displaystyle T\to 0}$ ми маємо,

${\displaystyle \left\langle n_{i}\right\rangle \to {\begin{cases}1&(\epsilon _{i}<\mu )\\0&(\epsilon _{i}>\mu )\end{cases}}.}$

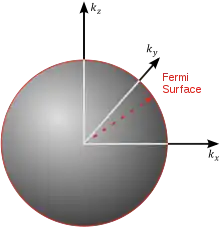
За принципом заборони Паулі два ферміони не можуть перебувати в одному стані. Тому в стані найнижчої енергії частинки заповнюють усі енергетичні рівні нижче енергії Фермі ${\displaystyle E_{\rm {F}}}$. Можна сказати ${\displaystyle E_{\rm {F}}}$ це енергетичний рівень, нижче якого є точно ${\displaystyle N}$ заповнених станів. У оберненому просторі ці частинки заповнюють певний об'єм, поверхня якого називається поверхнею Фермі.[8] Поверхня Фермі ідеального фермі-газу є сферою (Рис.1), радіус якої (модуль хвильового вектора Фермі)

${\displaystyle k_{\rm {F}}={\frac {p_{\rm {F}}}{\hbar }}={\frac {\sqrt {2m^{*}E_{\rm {F}}}}{\hbar }}=2\pi {{\left({\frac {3n_{v}}{8\pi }}\right)}^{{}^{1}\diagup {}_{3}}}}$,

визначається концентрацією електронів ${\displaystyle n_{v}=N/V}$, де ${\displaystyle p_{F}}$- імпульс Фермі, ${\displaystyle m^{*}}$- ефективна маса електрону, ${\displaystyle \hbar }$ — зведена стала Планка, ${\displaystyle V}$ - об'єм, що займає фермі-газ.

В металах рівень Фермі знаходиться у не повністю заповненій зоні - зоні провідності. Матеріал, рівень Фермі якого потрапляє в проміжок між енергетичними зонами (валентної зони та зони провідності), є ізолятором або напівпровідником залежно від ширини забороненої зони.

Рис. 2: Вид поверхні Фермі графіту в кутових Н точках зони Бріллюена, показує тригональну симетрію електронних і діркових кишень.

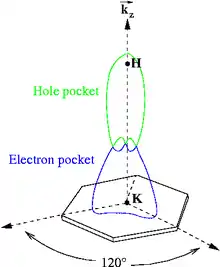
Поверхня Фермі матеріалів зі складною кристалічною структурою — складна періодична поверхня, яка у більшості металів безперервним образом проходить через всю обернену ґратку (відкрита поверхня Фермі). Замкнена поверхня Фермі періодично повторюється в кожній комірці оберненого простору. У тих випадках, коли в металі є декілька частково заповнених зон, поверхня Фермі розпадається на кілька поверхонь(за кількістю незаповнених зон), що розміщені в одній комірці.[6] Рисунок 2 ілюструє анізотропну поверхню Фермі графіту, який має на поверхні Фермі як електронні, так і діркові (з негативною ефективною масою) кишені через численні енергетичні зони, що перетинають енергію Фермі вздовж ${\displaystyle \mathbf {k} _{z}}$ напрямку.

Одним з методів, що враховує симетрію кристалу, побудови Фермі поверхні є наближення майже вільних електронів.[9][6] У нульовому наближенні поверхня Фермі є сукупністю сфер радіуса ${\displaystyle k_{\rm {F}}}$ з центрами у точках оберненого простору, що відповідають ${\displaystyle \mathbf {k} =2\pi \mathbf {K} }$, де ${\displaystyle \mathbf {K} }$ - довільний вектор оберненої ґратки. Часто в металах радіус поверхні Фермі ${\displaystyle k_{\rm {F}}}$ більше, ніж розмір першої зони Бріллюена, що призводить до того, що частина поверхні Фермі лежить у другій (або вище) зонах. Як і у випадку самої зонної структури, поверхню Фермі можна відобразити у схемі розширеної зони, де ${\displaystyle \mathbf {k} }$ дозволяється мати як завгодно великі значення, або в схемі зведеної зони, де хвильові вектори менше за модулем ${\textstyle {\frac {2\pi }{a}}}$ (у 1-вимірному випадку) де ${\displaystyle a}$ — стала ґратки. У тривимірному випадку схема зведеної зони означає, що для будь-якого хвильового вектора ${\displaystyle \mathbf {k} }$ існує відповідна кількість обернених векторів решітки ${\displaystyle \mathbf {K} }$, яка віднімається так, що новий вектор ${\displaystyle \mathbf {k} }$ тепер ближче до початку координат у ${\displaystyle \mathbf {k} }$ — просторі, ніж будь-який вектор ${\displaystyle \mathbf {K} }$.

Тверді тіла з великою щільністю станів на рівні Фермі стають нестабільними при низьких температурах і мають тенденцію утворювати основні стани, де енергія конденсації надходить від відкриття щілини на поверхні Фермі. Прикладами таких основних станів є надпровідники, феромагнетики, конфігурації Яна-Теллера та хвилі спінової щільності.

Результати теоретичного обчислення поверхонь Ферми багатьох металів наведені в Fermi Surface Database[4].

Електронні поверхні Фермі можна вивчати шляхом спостереження осциляцій термодинамічних і транспортних властивостей у магнітних полях ,${\displaystyle H}$, наприклад, ефект де Гааза–ван Альфена (дГвА) і ефект Шубникова–де Гааза (ШдГ). Перше — це коливання магнітної сприйнятливості, а друге — питомого опору. Коливання є періодичними з ${\displaystyle 1/H}$ і виникають через квантування енергетичних рівнів у площині, перпендикулярній до магнітного поля, явище, вперше передбачене Левом Ландау. Нові стани називаються рівнями Ландау і розділені енергією ${\displaystyle \hbar \omega _{\rm {c}}}$ де ${\displaystyle \omega _{\rm {c}}=eH/m_{c}c}$ називається циклотронною частотою, ${\displaystyle e}$ — це електронний заряд, ${\displaystyle m_{c}}$ — циклотронна маса електрона і ${\displaystyle c}$ — швидкість світла. У відомих роботах Ларс Онсагер [10] та Ілля Ліфшиць [11] довели, що період коливань ${\displaystyle \Delta H}$ пов'язаний з екстремальними (тобто максимальними або мінімальними) площинами поперечних перерізів поверхні Фермі перпендикулярно напрямку магнітного поля, ${\displaystyle S_{m}(\epsilon _{F})}$, за рівнянням Ліфшиця - Онсагера [12]

${\displaystyle S_{m}(\epsilon _{F})={\frac {2\pi e\Delta H}{\hbar c}}}$ .

Таким чином, визначення періодів коливань для різних напрямків прикладеного поля дозволяє визначити поверхню Фермі[13]. Спостереження коливань дГвА та ШдГ потребує магнітних полів, достатньо великих, щоб розмір циклотронної орбіти був меншим за середню довжину вільного пробігу.

Рис. 3: Поверхня Фермі BSCCO, виміряна за допомогою ARPES. Експериментальні дані представлені у вигляді графіка інтенсивності в жовто-червоно-чорній шкалі. Зелений пунктирний прямокутник представляє зону Бріллюена площини CuO₂ BSCCO .

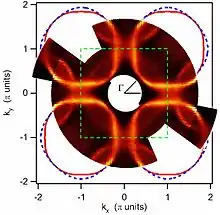
Найбільш безпосереднім експериментальним методом для визначення електронної структури кристалів у просторі імпульс-енергія (див. Обернена ґратка) і, отже, поверхні Фермі, є фотоелектронна спектроскопія з кутовим розділенням (ARPES, Angle-resolved photoemission spectroscopy). Приклад поверхні Фермі надпровідних купратів, виміряних за допомогою ARPES, показаний на Рис. 3.

Рис. 4: Поверхня Фермі міді в схемі зведеної зони, виміряна за допомогою 2D ACAR .[14]

За допомогою анігіляції позитронів також можна визначити поверхню Фермі, оскільки процес анігіляції зберігає імпульс початкової частинки. Відповідна експериментальна техніка називається кутовою кореляцією випромінювання анігіляції (ACAR, Angular Correlation of Annihilation Radiation), оскільки вона вимірює кутове відхилення від 7002180000000000000♠180 градусів обох квантів анігіляції. Таким чином можна зондувати щільність електронного імпульсу твердого тіла та визначити поверхню Фермі. Крім того, за допомогою спін-поляризованих позитронів можна отримати розподіл імпульсу для двох спінових станів у намагнічених матеріалах. ACAR має багато переваг і недоліків у порівнянні з іншими експериментальними методами: він не залежить від умов ультра високого вакууму, кріогенних температур, високих магнітних полів або повністю впорядкованих сплавів. Однак ACAR потребує зразків з низькою концентрацією вакансій, оскільки вони діють як ефективні пастки для позитронів. Таким чином в 1978 році було отримано перше визначення розмитої поверхні Фермі в 30 % сплаві. Поверхня Фермі міді, що була відбудована за допомогою ACAR, приведена на Рис.4.