Зоногон

Багатокутник, не є зоногоном, але має лише одну пару не паралельних сторін і лише одну пару не рівних сторін. Пунктиром показана сторона зоногона, який вийде, якщо додати будь-яку з умов.

Зоногон на малюнку є сумою Мінковського помаранчевих відрізків: до будь-якої його точки існує шлях з векторів, подібних фіолетовим, що лежать на цих відрізках. Вони не обов'язково повинні мати спільну вершину, як на малюнку, оскільки сума Мінковського множин не залежить від їх паралельного перенесення.

Межа проєкції на площину чотиривимірного гіперкуба утворює в загальному випадку зоногон з вісьмома сторонами.

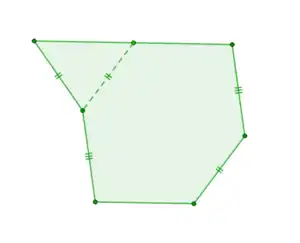
• Зоногон — опуклий багатокутник з парною кількістю сторін, які можна розбити на пари рівних і паралельних. Насправді, достатньо вимагати істинність обох умов для всіх пар сторін, крім однієї — для неї умова вже буде наслідком, що неважко довести за індукцією за кількістю сторін багатокутника. Однак пара сторін, паралельність і рівність яких не постулюється, обов'язково повинна бути однією і тією ж для обох умов, інакше багатокутник вже не обов'язково буде зоногоном: приклад багатокутника, який не є зоногоном, у якому протилежні сторони лише однієї пари не паралельні і протилежні сторони лише однієї пари не рівні, зображений на рисунку.
• Зоногон — опуклий багатокутник з парною кількістю сторін, у якого всі протилежні сторони і кути рівні.
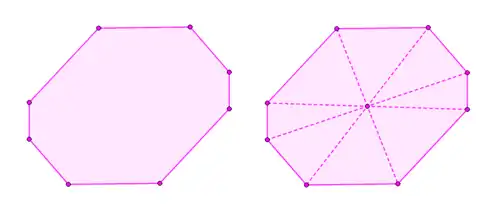
• Зоногон — сума Мінковського скінченного числа відрізків на площині. Кількість сторін отриманого зоногона дорівнює подвоєній кількості відрізків.
• Зоногон — межа проєкції на площину гіперкуба певної розмірності. Це визначення можна отримати з попереднього, користуючись тим фактом, що гіперкуб є сумою Мінковського своїх ребер, які виходять з однієї вершини, і тим, що проєкція суми Мінковського відрізків (як і будь-яких інших множин) є сумою Мінковського їхніх проєкцій. За розмірності гіперкуба ${\displaystyle n}$ отриманий зоногон має рівно ${\displaystyle 2n}$ сторін у загальному випадку і не більше ${\displaystyle 2n}$ сторін у будь-якому випадку. Важливо, що гіперкуб розмірності ${\displaystyle n}$ не обов'язково повинен проєктуватися з ${\displaystyle n}$-вимірного простору на площину, що міститься в цьому просторі: наприклад, проєктуючи куб з ребром ${\displaystyle 2}$ з тривимірного простору на площину, що міститься в ньому, можна отримати фігуру з діаметром менше ${\displaystyle 2}$, оскільки такий діаметр вписаної сфери куба, чия проєкція є колом діаметра ${\displaystyle 2}$ і міститься всередині проєкції самого куба за будь-якого його положення, а ось ортогональна проєкція куба такого самого розміру з вершинами ${\displaystyle (0,0,\pm 1,\pm 1,\pm 1)}$ з п'ятивимірного простору на площину, утворену усіма точками вигляду ${\displaystyle (x,y,0,0,0)}$, складається взагалі з однієї точки — ${\displaystyle (0,0,0,0,0)}$. Це уточнення впливає не тільки на розмір одержуваних зоногонів — деякі зоногони з точністю до подібності можна отримати тільки проєктуванням гіперкуба на площину з простору більшої розмірності, ніж розмірність самого гіперкуба.

• Паралелограм — чотирикутник, що є зоногоном. Зокрема, зоногони — це ромб, прямокутник та квадрат.
• Правильний багатокутник з парною кількістю сторін є зоногоном.

• Узагальнення теореми Монскі: ніякий зоногон не можна розрізати на непарну кількість рівних за площею трикутників. Цей факт довів той самий Пауль Монскі після основної теореми[1][2].

• Максимальна кількість пар вершин, які можуть міститись на однакових відстанях, у зоногоні з ${\displaystyle n}$ сторонами дорівнює ${\displaystyle 2n-3}$. Існують зоногони з кількістю таких пар, рівною ${\displaystyle 2n-O({\sqrt {n}})}$ (див. «O» велике і «o» мале)[3].

• Будь-який строго опуклий зоногон з ${\displaystyle 2n}$ сторонами можна розбити на ${\displaystyle {\binom {n}{2}}={\frac {n(n-1)}{2}}}$ паралелограмів, причому серед них завжди на кожну пару можливих напрямків сторін зоногона припадатиме рівно один паралелограм з такими самими напрямками сторін[4]. Кількості таких можливих розбиттів для зоногонів з будь-якими кількостями сторін дає послідовність A006245 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.

• Для будь-якого довільного розбиття зоногона на паралелограми (в будь-якій можливій їх кількості) знайдеться принаймні три вершини зоногона, кожна з яких належить лише одному з паралелограмів[5].

Відсікання шару паралелограмів (чотирикутних зоногонів).

Відсікання двох протилежних вершин зоногона.

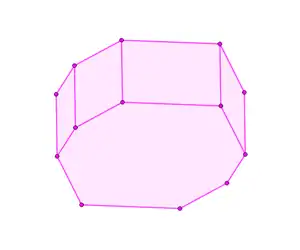
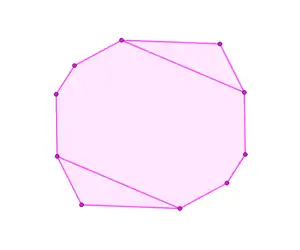
Зазначені способи можна застосувати в індукції за кількістю сторін зоногона для доведення наведених вище еквівалентних визначень і властивостей.

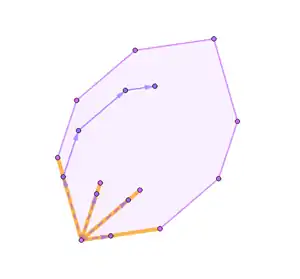
• Відсікання вершин — за допомогою нього, наприклад, легко доводиться еквівалентність головного визначення другому визначенню з розділу з еквівалентними визначеннями.
• Відсікання смуг паралелограмів — крім іншого, його можна використати для доведення властивостей вище, пов'язаних з розбиттям зоногонів на паралелограми повністю.

Усі зоногони з кількістю вершин, більшою від чотирьох, у замощеннях нижче можна розбити на зоногони з меншою кількістю вершин за допомогою розсікання шарів паралелограмів, показаного на одному з малюнків вище. Також ці паралелограми можна видалити із замощення, що буде рівносильно «складанню» зоногонів у певному напрямку.

Замощення одним типом зоногонів

Чотирикутник і шестикутники, які є зоногонами, є також паралелогонами і допускають замощення площини власними копіями, отриманими тільки за допомогою паралельного перенесення.

Замощення площини одним типом зоногонів
Замощення чотирикутними зоногонами	Замощення шестикутними зоногонами

Замощення двома типами зоногонів

Такі замощення є свого роду зрізаними замощеннями площини паралелограмами (чотирикутними зоногонами) по ребрах і по вершинах відповідно.

Замощення площин двома типами зоногонів
Замощення чотирикутними і шестикутними зоногонами	Замощення чотирикутними і восьмикутними зоногонами

Деякі інші замощення

Замощення площини декількома типами зоногонів, включно з восьмикутними, отримані з замощень площини одним типом зоногонів
Замощення чотирикутними і восьмиукутними зоногонами	Замощення чотирикутними, шестикутними і восьмикутними зоногонами
Каркаси
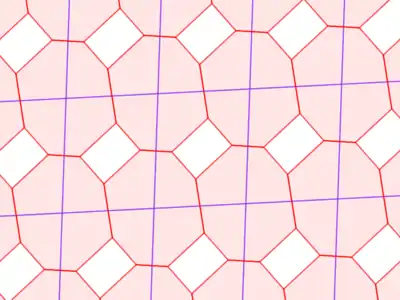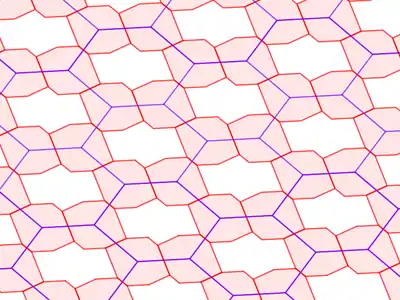Замощення
У загальному випадку восьмикутний зоногон задає два подібних замощення.	У загальному випадку восьмикутний зоногон задає чотири подібних замощення.

Замощення площини чотирикутними, шестикутними і восьмикутними зоногонами, отримані з замощень попередньої таблиці
Замощення, отримане з замощення чотирикутними і восьмикутними зоногонами	Замощення, отримане з замощення чотирикутними, шестикутними і восьмикутними зоногонами
Каркаси
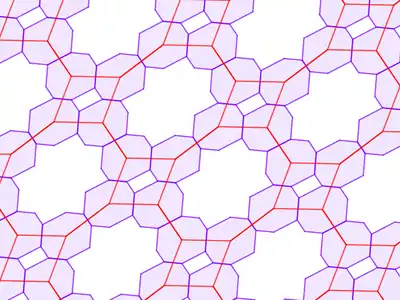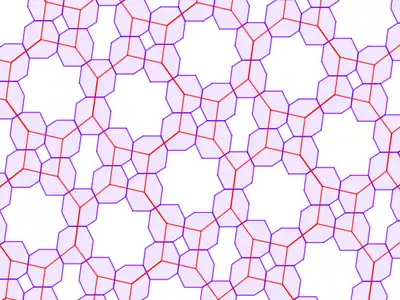Замощення
У загальному випадку восьмикутний зоногон задає чотири подібних замощення (двома способами можна з'єднувати самі восьмикутники, а ще двома для кожного розташування восьмикутників згрупувати решту частини площини в чотирикутники і шестикутники).	У загальному випадку восьмикутний зоногон задає чотири подібних замощення, як і у випадку зліва. У цій мозаїці, на відміну від тієї, що зліва, чотирикутники, які беруть участь у заповненні дірок у «кільцях» з восьми восьмикутників, збігаються з чотирикутниками, які заповнюють дірки в «кільцях» з чотирьох восьмикутників — цей факт ілюструє можливість двоякого заповнення «кілець» з восьми восьмикутників (у другому варіанті їх чотирикутники збігалися б з чотирикутниками з «кілець» з шести восьмикутників).

Деякі способи «розсування» замощень

Замощення можна «розсунути» вздовж періодичних розрізів між багатокутниками, а отримані щілини можна заповнити смугами, наведеними нижче.

Способи з рівномірним чергуванням сторін
Період 1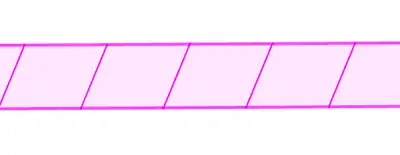
Період 2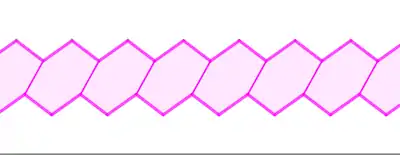
Період 3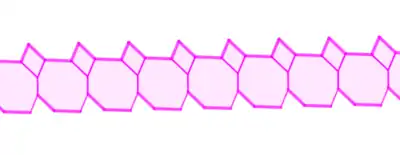
Період 4		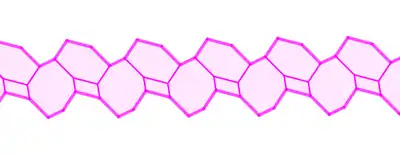За допомогою цієї смуги ліве замощення з першої таблиці попереднього розділу можна перетворити на праве замощення тієї ж таблиці.

Способи зі сторонами, зустрічаються з різною частотою
Період 4		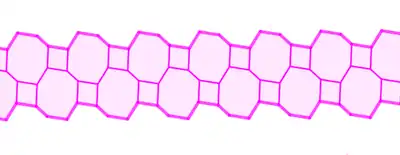На межі цієї смуги один тип сторін зустрічається в два рази частіше, ніж будь-який з інших двох.

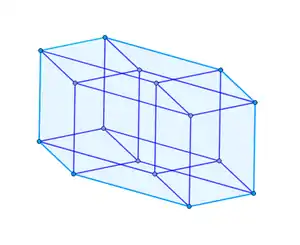
• Зоноедр (зонотоп) — багатогранник, який є узагальненням зоногона для тривимірного простору та просторів більшої розмірності. Іноді під зоноедром мають на увазі тільки тривимірний багатогранник, а під зонотопом — багатогранник довільної розмірності.
• Можна розглядати центрально-симетричний багатокутник, що не є опуклим і навіть несамоперетинним. При цьому для нього будуть істинними тільки два перших визначення з розділу Еквівалентні визначення відповідно до прибраних вимог опуклості. У певному сенсі такі багатокутники з невеликою кількістю сторін все ще будуть допускати замощення площини.