Конус (топологія)

• Конус над точкою ${\displaystyle p}$ дійсної прямої — інтервал ${\displaystyle \{p\}\times [0,1]}$.
• Конус над інтервалом дійсної прямої — трикутник (2 -симплекс).
• Конус над многокутником ${\displaystyle P}$ — піраміда з основою ${\displaystyle P}$.
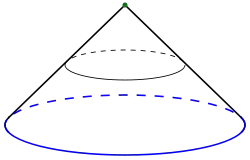
• Конус над кругом — класичний конус (заповнений всередині).
• Конус над колом — бокова поверхня конуса над кругом:

${\displaystyle \{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}=z^{2}\wedge 0\leqslant z\leqslant 1\}}$,

що є гомеоморфною кругу.

• У загальному випадку конус над гіперсферою є гомеоморфним замкнутій ${\displaystyle (n+1)}$-вимірній кулі.
• Конус над ${\displaystyle n}$-симплексом є ${\displaystyle (n+1)}$-симплексом.

• Конус ${\displaystyle \mathrm {C} X}$ може бути сконструйований як циліндр постійного відображення ${\displaystyle X\to \{0\}}$.
• Всі конуси є лінійно зв'язними, оскільки будь-яку точку можна з'єднати з вершиною. Більш того, будь-який конус є стягуваним до вершини за допомогою гомотопії, що задається формулою ${\displaystyle h_{t}(x,s)=(x,(1-t)s)}$.
• Якщо ${\displaystyle X}$ є компактним і гаусдорфовим, то конус ${\displaystyle \mathrm {C} X}$ можна подати як простір відрізків, що з'єднують кожну точку ${\displaystyle X}$ з єдиною точкою; якщо ${\displaystyle X}$ не є компактним або гаусдорфовим, то це не так, оскільки в загальному випадку топологія на фактор-просторі ${\displaystyle \mathrm {C} X}$ буде сильнішою, ніж на множині відрізків, що з'єднують ${\displaystyle X}$ з точкою.
• В алгебричній топології конуси широко застосовуються завдяки тому, що за їм допомогою простір вкладається в стягуваний простір; в зв'язку з цим також важливим є наступний результат: простір ${\displaystyle X}$ є стягуваним тоді і тільки тоді, коли він є ретрактом свого конуса.

Відображення ${\displaystyle X\mapsto \mathrm {C} X}$ породжує конічний функтор ${\displaystyle \mathrm {C}$ :\mathbf {Top} \to \mathbf {Top} } над категорією топологічних просторів ${\displaystyle \mathbf {Top} }$.

Наведений конус - конструкція над топологічними просторами із виділеною точкою ${\displaystyle (X,x_{0})}$:

${\displaystyle \mathrm {C} (X,x_{0})={\big (}X\times [0,1]{\big )}/{\big (}(X\times \left\{0\right\})\cup (\left\{x_{0}\right\}\times [0,1]){\big )}}$.

Природне вкладення ${\displaystyle x\mapsto (x,1)}$ дозволяє розглянути будь-який топологічний простір із виділеною точкою як замкнуту підмножина свого редукованого конуса.

• Джойн (топологія)
• Надбудова (топологія)
• Стягуваний простір

• Allen Hatcher, Algebraic topology. Cambridge University Press, Cambridge, 2002. xii+544 pp. ISBN 0-521-79160-X and ISBN 0-521-79540-0