Молекулярна вітроенергетика

Молекулярна вітроенергетика (англ. molecular wind power) – складова частина молекулярної енергетики, що вивчає та використовує відновлювані енергетичні властивості швидких молекул, атомів, йонів, інших малих частинок газового повітряного середовища, взаємодію цих частинок між собою, з іншими тілами а також з електричними та магнітними полями з метою вироблення, накопичення, передачі та розподілу електричної енергії.

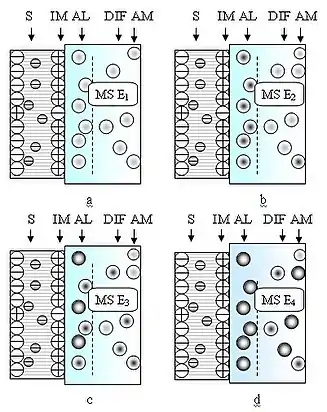
Обмін енергією швидких молекул повітря прикордонного та дифузного шарів з молекулами твердого тіла.

Ключовим поняттям молекулярної вітроенергетики є молекулярна система енергії – певний об'єм газової повітряної суміші, що володіє точно визначеними фізико-хімічними параметрами та характеристиками, зокрема, внутрішньою енергією молекул газової повітряної суміші, швидкістю, довжиною вільного пробігу, частотою співударів молекул та їх енергією на кордоні фаз. У рамках молекулярної вітроенергетики вивчаються молекулярні системи повітряної газової суміші, встановлюються їх енергетичні параметри та характеристики, створюються та досліджуються способи (технології) молекулярної вітроенергетики та технічні системи (засоби) молекулярної вітроенергетики, які дозволяють перетворити кінетичну енергію теплового руху швидких молекул повітря в електричну енергію безпосередньо або ж опосередковано.

Молекулярна вітроенергетика є також складовою частиною класичної вітроенергетики, в основі якої лежать закони газодинаміки (аеродинаміки), що описують рух повітря та його взаємодію з твердими тілами, а також закони аеростатики, що оцінюють рівновагу повітря та його дію на занурені в нього тіла. У розрахунках параметрів та характеристик систем молекулярної вітроенергетики поряд з енергетичними характеристиками швидких молекул повітря, силами взаємодії цих молекул між собою та з іншими тілами використовуються макроскопічні параметри (швидкість, тиск, густина) потоків повітря. Резерви внутрішньої енергії, що криються в газовому повітряному середовищі, суттєво перевищують рівні енергії, які сьогодні доступні для освоєння макроскопічними вітроенергетичними технологіями.

Для ефективного перетворення енергії молекул газової повітряної суміші в електричну енергію можна використати відомі фізичні явища: йонізації атомів та молекул активної речовини під дією швидких молекул повітря, зокрема, явище ступінчато-ударної йонізації; термоелектричний ефект Зеебека – виникнення термо-ЕРС у молекулярній структурі під тепловою дією швидких молекул повітря; сорбційний ефект – виникнення термо-ЕРС у сорбційній молекулярній структурі при поглинанні швидких молекул повітря; прямий п’єзоелектричний ефект – виникнення електричних зарядів на гранях певних кристалів при деформації та зворотний магнітострикційний ефект (магнетопружний ефект Вілларі) – зміна намагніченості певних матеріалів під впливом механічних напружень. Ці фізичні явища окремо або ж у поєднанні з іншими застосовні для створення високоефективних молекулярних систем вітроенергетики. В основі роботи молекулярних систем вітроенергетики лежать закони молекулярної фізики, кінетичної теорії газів, квантової хімії, фізики і хімії поверхні, молекулярної гідродинаміки, термодинаміки та електродинаміки, хімічного інжинірингу та матеріалознавства.

Методологія розрахунків та побудови ключових енергогенеруючих елементів молекулярної вітроенергетики відрізняється від звичних підходів, які використовуються при створенні систем класичної вітроенергетики. [1] [2]

Історія

Газ по своїй природі має багато спільного з рідиною, тож, зважаючи на кореляцію багатьох характеристик, гази та рідини переважно досліджувалися в одному часовому полі. Перше систематичне викладення поведінки газів належить французькому фізику та інженеру Бенуа Полю Емілю Клапейрону та шотландському фізику Джону Джеймсу Уотерстоуну. Еміль Клапейрон 1834 року, аналізуючи роботи своїх попередників Роберта Бойля, Едма Маріотта, Жозефа Луї Гей-Люссака, Жака Шарля а також Амедео Авогадро, вивів рівняння стану ідеального газу [3]. Німецький фізик та хімік Юліус Роберт фон Маєр [4]встановив зв'язок між теплоємностями для ізобаричних та ізохоричних процесів у газах. Джон Джеймс Уотерстоун доказав, що тиск газу в одиниці об’єму залежить від кількості молекул та від середньої квадратичної швидкості молекул, і фактично вивів закон ідеального газу. [5] Проте, сучасну кінетичну теорію газів сформулював у 1856 році німецький хімік і фізик Август Креніг. [6] Німецький фізик Рудольф Клаузіус , який працював в області термодинаміки, узагальнив відомі факти, ввів у користування поняття ентропії й створив більш фундаментальну теорію, що враховувала поступальний, обертовий та коливальний рухи молекул. Ним же запропоновано поняття довжини вільного пробігу частинки. [7][8] Джеймс Клерк Максвелл визначив розподіл молекул за швидкостями. [9] У 1866 році австрійський фізик Людвіг Больцман отримав рівняння рівноважного розподілу молекул ідеального газу за імпульсами та координатами, а 1871 року узагальнив цей розподіл для частинок у зовнішньому полі.

Вільям Томсон лорд Кельвін спільно з Джеймсом Прескоттом Джоулем провели охолодження газів при розширенні без здійснення роботи, яке послужило перехідним ступенем від теорії ідеальних газів до теорії реальних газів. Важливими етапами розвитку газової теорії стали дослідження міжмолекулярної взаємодії та створення голландським фізиком Яном Дидериком ван дер Ваальсом теорії фазових переходів між газоподібним та рідинним станами речовини, побудова теорії Броунівського руху Альбертом Ейнштейном та роботи з теорії Броунівського руху й теорії флуктуацій Мар'яна Смолуховського.

Моделі ідеального та реального газів дозволяли розвивати прикладні напрямки досліджень, зокрема, технології теплових двигунів. Пізніше дослідження поведінки газів були спрямовані на вивчення фазових та критичних станів речовини, вакуумної та пневматичної техніки, газорозрядних ламп, газогонів, забруднення атмосфери та парникового потепління на основі фізичних та математичних моделей ідеальних та реальних газів. Досліджувалися процеси, що протікають в атмосферному повітряному середовищі, та сили, які супроводжують ці процеси. Розраховувалися енергетичні параметри газової повітряної суміш та знаходилися відхилення енергетичних параметрів суміші реальних та ідеальних газів. Вивчалися особливості взаємодії швидких молекул повітря з речовиною та можливість використання їх кінетичної енергії для виробництва електричного струму.

Негативні чинники, які характерні для макроенергетики вітру, стимулювали появу молекулярної вітроенергетики (англ. molecular wind power) – складової частини молекулярної енергетики, що вивчає та використовує відновлювані енергетичні властивості швидких молекул, атомів, йонів, інших малих частинок газового повітряного середовища, взаємодію цих частинок між собою, з іншими тілами а також з електричними та магнітними полями з метою вироблення, накопичення, передачі та розподілу електричної енергії.

Фізичні основи

Повітряна газова суміш

У фундаменті молекулярної вітроенергетики лежить атомно-молекулярний принцип побудови речовини. Він характеризує дискретність або перервність і розкриває взаємодію атомів та молекул газової суміші між собою та з оточуючими тілами. Ключовими поняттями молекулярної вітроенергетики є атом, молекула, хімічний зв'язок, газова повітряна суміш, молекулярна система енергії газоповітряної суміші, молекулярні технології та системи вітроенергетики.

Повітря – мутуюче газове середовище, яке зазнає постійних змін. Стійких зв’язків між молекулами повітряного середовища немає, тож, молекули неперервно рухаються. Взаємодія молекул характеризується потенціальною енергією E_P(r) [Дж]. Вона визначається роботою, яку необхідно виконати силам F(r) [Н] при переміщенні молекули від заданого положення до безкінечності, де вважається, що E_P(r) = 0. Якщо дві молекули зближуються на відстань Δr [м], то робота, що виконується, дорівнює ΔА = F(r)·Δr [Дж] і є позитивною. Зростання кінетичної енергії молекул супроводжується зменшенням їх потенціальної енергії у відповідності до закону збереження енергії. Співвідношення між значенням потенціальної енергії E_P(r₀) та середньою кінетичною енергією молекули газу E_K [Дж] має вигляд

E_K » E_P(r₀).

У газі між молекулами майже немає взаємодії, тому вони володіють великою кінетичною енергією E_K [Дж], що значно перевищує їх потенціальну енергію E_P [Дж]. У проміжках між зіткненнями молекули рухаються прямолінійно.

Молекули газу, як і їх родичі в рідині, також утворюють молекулярні колективи, проте, вони ще менш стійкі, ніж в рідині. Локальні флуктуації в повітряному середовищі неминучі. Навіть мала тінь у палючих променях Сонця створює на межі зі світлом різницю температур та відчутний рух повітря. Газ є термодинамічним утворенням. Для нього характерні термодинамічні процеси перенесення – дифузія, теплопровідність, внутрішнє тертя, поверхневі явища на кордоні фаз та критичний стан. Процеси перенесення в газовому середовищі визначаються будовою та взаємодією його молекул.

На малих відстанях (~ 10^–9 м) між молекулами діють сили тяжіння, на відстанях ~ 10^–10 м – сили відштовхування. Згідно теорії голландського фізика Яна Дидерика ван дер Ваальса, сила міжмолекулярної взаємодії F [Н] є рівнодіючою сил тяжіння та відштовхування й залежить від відстані r [м] так

F(r) = –а/r⁶ при r > r₀;

F(r) = 0 при r = r₀;

F(r) = b/r^m при r < r₀,

де а та b – коефіцієнти.

На відстані r = r₀ сили тяжіння молекул урівноважуються силами відштовхування. Сили тяжіння, що убувають зворотно пропорційно шостого степеня відстані між молекулами F(r) = –а/r⁶ при r > r₀, звуться силами ван дер Ваальса. Вони виникають при взаємодії незаряджених атомів та молекул, викликають когезію та адгезію конденсованої фази а також адсорбцію газів і є причиною тяжіння макроскопічних тіл.

Сили ван дер Ваальса пояснюються певною мірою слабкими хімічними зв’язками. До слабких хімічних зв’язків належать диполь-дипольна взаємодія Кеезома, індукційна взаємодія Дебая, дисперсійна взаємодія Лондона та водневий зв'язок.

Модель суміші ідеальних газів

Модель ідеального газу.

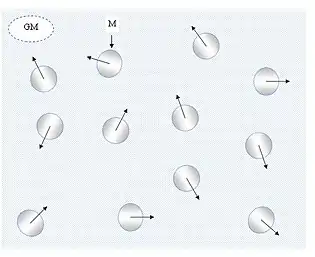
При розгляді суміші реальних газів, якою є повітря, прийнято користуватися спрощеними фізичними моделями, зокрема, поняттям ідеального газу. У цій моделі відстань між молекулами значно перевищує їх розміри, тож вони находяться в неперервному русі, між молекулами немає сил тяжіння (відштовхування), і вони практично не взаємодіють між собою. Потенціальну енергію взаємодії матеріальних часток, що складають газ, вважають мізерною, порівнюючи з їх кінетичною енергією. Зіткнення частинок між собою та з оточуючими тілами абсолютно пружні, а час взаємодії дуже малий, порівнюючи із середнім інтервалом між зіткненнями. Тиск газу є результатом співударів молекул газу з поверхнею стінки судини. Такі спрощення дозволяють нормалізувати багатофакторну систему газової суміші й спростити розрахунки.

Стан ідеального газу в загальному вигляді описується рівнянням Еміля Клапейрона, яке він вивів емпірично у 1834 році на основі аналізу робіт своїх попередників Роберта Бойля, Едма Маріотта, Жозефа Луї Гей-Люссака, Жака Шарля та Амедео Авогадро,

р·V = m·R_SP·T,

де р [Па] – тиск; V [м³] – об'єм, Т [К] – температура; m [кг] – маса газу, R_SP [Дж/(кг·К)] – індивідуальна газова стала, яка є характерною для кожного газу.

Це рівняння можна записати через кількість речовини n_M,

р·V = n_M·R·T = (m/M)·R·T,

де M [кг/моль] – молярна маса, а R [Дж/(кг·К)] – універсальна газова стала.

У статистичній механіці використовується ймовірнісний підхід при розгляді великого числа атомів та молекул, для однокомпонентного ідеального газу останнє рівняння має вигляд

р·V = N·k_B·T,

де k_B [Дж/К] – стала Больцмана, а N – число молекул газу.

Індивідуальна газова стала R_SP [Дж/(К·моль)] зв'язана з універсальною газовою сталою R [Дж/(К·моль)] відношенням

R_SP = R/М [Дж/(кг·К)].

Індивідуальна газова стала повітря – R_AIR = 287,2 Дж/(кг·К).

Терміни молекулярна маса та відносна молекулярна маса є синонімами. Для того щоб обчислити відносну молекулярну масу речовини, потрібно скласти відносні атомні маси атомів усіх елементів, які входять до складу молекули. При цьому слід обов'язково враховувати число атомів кожного елемента, що входять до складу молекули. Термін відносна молекулярна маса не може вживатися для йонних сполук, бо вони не містять молекул. У цьому разі вживають термін відносна формульна маса. Відносну формульну масу обчислюють так само, як і відносну молекулярну масу.

Нормальним станом газу вважають фізичні умови, які визначаються нормальними значеннями тиску р₀ = 101325 [Па], температури Т₀ = 273,15 К та молярного об’єму газу V_M = 22,41383·10^–3 м³/моль. У нормальному стані в 1 м³ будь-якого газу міститься однакове число молекул (число Лошмідта N_L [м^–3]). Число Лошмідта вираховується через число Авогадро N_A та молярний об'єм V_M [м^–3],

N_L = N_A/V_M = 2,686754·10²⁵ м^–3.

Універсальна газова стала R [Дж/(К·моль)] може бути визначена через параметри нормального стану газу,

R = р₀·V_M/T₀ = 8,31441,

де р₀ [Па] та T₀ [К] – тиск та температура газу в нормальному стані.

Значення сталої Больцмана k_B [Дж/К] зв’язано з універсальною газовою сталою R [Дж/(К·моль)],

k_B = R/N_A = 1,380622·10^–23 [Дж/К].

Маса окремої молекули газу m₀ [кг] визначається через молярну масу М [кг/моль],

m₀ = М/N_A .

Кількість речовини n_M [моль] можна знайти як відношення числа N атомів або молекул речовини до сталої Авогадро N_A,

n_M = N/N_A.

Ідеальний газ є ізотропним, всі напрямки в ньому еквівалентні, а властивості у всіх напрямках однакові. Встановимо зв’язок між тиском р [Па] та середньою кінетичною енергією Е_K [Дж] поступального руху молекули газу,

р = (2/3)·n₀·m·υ²/2 = (2/3)·n₀·Е_K.

де n₀ – середня концентрація молекул газу.

Помножимо ліву та праву частини рівності (8.26) на об’єм моля V_М [м³/моль],

р·V_М = (2/3)·n₀·V_М·Е_K = (2/3)·N_А·Е_K

де N_А – число Авогадро, N_А = n₀·V_М.

Виходячи з рівняння Клапейрона (8.18), у попередньому виразі зробимо заміну

р·V_М = R·T,

де R – універсальна газова стала, R = 8,3155 Дж/(моль·К).

Отже

(2/3)·N_А·Е_K = R·T.

Звідси можна визначити середню кінетичну енергію молекули Е_k [Дж],

Е_K = (3/2)·(R/N_А)·T = (3/2)·k_B·T,

де k_B [Дж/К] – стала Больцмана,

Якщо врахувати обертальні та коливальні ступені вільності, вираз (8.30) для середньої кінетичної енергії молекули Е_K [Дж] набирає такого вигляду

Е_K = (і/2)·k_B·T,

де і – загальне число ступенів вільності, для молекул одноатомного газу і = 3 (поступальні ступені вільності), для багатоатомних молекул враховуються також обертальні ступені вільності, для двохатомних молекул – і = 5, для багатоатомних молекул – і = 6.

Внутрішня енергія ідеального газу U_M [Дж] складається з кінетичних енергій окремих молекул, вона дорівнює добутку числа Авогадро N_A на середню кінетичну енергію однієї молекули E_K [Дж],

U_M = N_A·E_K = (і/2)·N_A·k_B·T = (і/2)·R·T.

Внутрішня енергія U [Дж] довільної маси газу m [кг] дорівнює внутрішній енергії моля U_M [Дж], помноженій на число молів n_M, які містяться в цій масі,

U = (m/M)·U_M = (m/M)·(і/2)·R·T = n_M·(і/2)·R·T,

де n_M [моль] – кількість речовини, n_M = m/M.

Теплоємністю С_Н [Дж/К] називають кількість теплоти Q_Н [Дж], яка потрібна для нагрівання певної маси на один градус температури,

С_Н = dQ/dT.

Розрізняють молярну С_Н [Дж/(моль∙К)] та питому с_Н [Дж/(кг∙К)] теплоємності речовини, які пов’язані між собою через молярну масу М [кг/моль],

С_Н = М·с_Н.

Молярну теплоємність при сталому об’ємі позначають С_НV, молярну теплоємність при сталому тиску – С_НР. Якщо нагрівання відбувається при сталому об’ємі, тіло не здійснює роботи над зовнішніми тілами, тож вся теплота витрачається на приріст внутрішньої енергії тіла dU [Дж],

dQ = dU.

Молярна теплоємність С_НV [Дж/(моль∙К)] будь-якого тіла при сталому об’ємі дорівнює

С_НV = dU_M/dТ.

Молярна теплоємність ідеального газу при сталому об’ємі С_НV [Дж/(моль∙К)] залишається величиною сталою та не залежить від параметрів стану газу,

С_НV = (і/2)·R.

Визначимо молярну теплоємність газу С_НP [Дж/(моль∙К)] при сталому тиску. Для цього скористаємося законом збереження енергії для термодинамічної системи,

dQ_MP = dU_M + dW [Дж].

де dW [Дж] – робота, яку виконує газ при розширенні.

При р = const ця робота визначається формулою

dW = p·dV.

де dV [м³] – зміна об’єму газу при нагріванні його на один градус при р = const.

Тоді, поділивши ліву та праву частини рівняння, яке описує закон збереження енергії, на dT, отримуємо

С_НP = С_НV + p·dV/dT.

З метою визначення dV [м³] використаємо рівняння стану для моля газу: p·V = R·T; V = R·T/р. Звідси

dV = R·dT/р.

Підставивши значення dV [м³] в узагальнений вираз теплоємності, дістанемо рівняння Роберта Майєра– німецького фізика, який обґрунтував перший закон термодинаміки та вичислив механічний еквівалент теплоти,

С_НP = С_НV + R.

Робота, яку здійснює 1 моль ідеального газу при підвищенні його температури на один градус, дорівнює універсальній газовій сталій. З урахуванням останньої формули отримуємо

С_НP = [(і + 2)/2]·R.

Поділивши С_НP на С_НV, знайдемо показник адіабати γ – характерне для кожного газу відношення,

γ = С_НP/С_НV = (і + 2)/2.

Із двох останніх рівнянь витікає

С_НV + R = С_НV·γ

або

С_НV = R/(γ – 1).

Молярна теплоємність одноатомного ідеального газу при постійному об’ємі дорівнює C_НV = (3/2)·R = 12,5 Дж/(моль∙К). Молярна теплоємність одноатомного ідеального газу при постійному тиску дорівнює C_НP = C_HV + R = (5/2)·R = 20,8 Дж/(моль∙К). Молярна теплоємність двоатомного ідеального газу при постійному об’ємі дорівнює C_НV = (5/2)·R = 20,75 Дж/(моль∙К). Молярна теплоємність поліатомного ідеального газу при постійному об’ємі дорівнює C_HV = 3·R = 24,9 Дж/(моль∙К). У рівноважному стані параметри газу залишаються незмінними, проте, взаємне розташування молекул та їхні швидкості безперервно змінюються. Закон розподілу молекул за швидкостями є статистичним, бо він стосується сукупності молекул.

Швидкість v_i [м/с], яка відповідає максимуму кривої розподілу швидкостей молекул, називається найімовірнішою швидкістю,

v_i = √(2·R·T/M),

де R [Дж/К] – універсальна газова стала, Т [К] – абсолютна температура, M [кг/моль] – молярна маса.

Середня квадратична швидкість ‹v_S› [м/с] та середня арифметична швидкість ‹v› [м/с] обчислюються за допомогою формул

‹v_S› = √v_S² = √(3·R·T/M);

‹v› = √[8·R·T/(π·M)].

Названі швидкості різняться між собою,

v_i < ‹v› < ‹v_S›.

Молекули газу взаємодіють між собою за допомогою сил, які на великих відстанях між молекулами є силами тяжіння, що швидко убувають зі збільшенням відстані між молекулами. На малих відстанях ці сили є силами відштовхування.

Середня кількість зіткнень молекул газу повітряної суміші дорівнює z = 10⁹-10¹⁰ с^–1. Відстань, яку проходить молекула між двома послідовними зіткненнями, зветься середньою довжиною вільного пробігу l_MFP [м]. Вона дорівнює відстані ‹v›·Δt, яку проходить молекула за час Δt [с], віднесеній до числа зіткнень z за цей же час,

l_MFP = ‹v›·Δt/z [м].

де ‹v› [м/с] – середня швидкість молекул, z [с^–1] – число зіткнень за час Δt [с].

Тиск газу є результатом зіткнень великої кількості молекул зі стінками судини, в якому газ знаходиться.

Для газу виконується закон Клаузіуса-Максвелла [60-62]: енергія молекули рівномірно розподілена між всіма ступенями свободи. На кожну ступінь свободи припадає в середньому однакова кінетична енергія. Основне рівняння кінетичної теорії газів зв’язує тиск р [Па] та об’єм V [м³] газу з повною кінетичною енергією поступального руху його молекул. Абсолютному нулю температури відповідає енергія, що є рівною нулю.

У суміші газів кожен газ створює той тиск, який би він створював у самоті. Тиск суміші газів дорівнює сумі парціальних тисків окремих газів p₁, p₂, p₃,.., p_i [Па],

p = p₁ + p₂ + p₃+ …+ p_i.

Тиск суміші газів можна виразити через концентрації молекул речовини n₁, n₂, n₃,.., n_i [м^–3],

p = n₁·k_B·T + n₂·k_B·T + n₃·k_B·T + …+ n_i·k_B·T.

Це рівняння можна переписати у вигляді

p = (n₁ + n₂ + n₃ + …+ n_i)·k_B·T.

Ідеальний газ є гіпотетичною моделлю, яка підкоряється рівнянню Клапейрона,

р·V/(n_M·R·T) = 1.

Рівняння Клапейрона описує газ при високих температурах і низьких тисках, коли газ знаходиться в умовах, досить далеких від конденсації. При високих температурах і тиску молекули газу поглинають енергію, збільшується вібрація та обертання молекул.

Для реальних газів гармонія порушується.

Модель суміші реальних газів

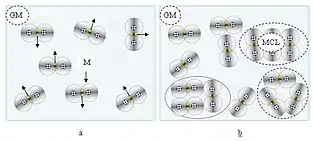
Наближення до моделі реального газу двоатомних молекул. Перехід від слабкої взаємодія молекул до сильної взаємодії молекул.

При зниженні температури або при підвищенні тиску спостерігається відхилення від законів ідеального газу. Зростає взаємодія молекул між собою. Сильно проявляються також сили відштовхування на малих відстанях та тяжіння на великих. У разі сильної взаємодії молекули газу починають вести себе подібно конденсованій речовині. Деякі з них злипаються та утворюють молекулярні кластери, як це спостерігається в рідині. Коли температура та тиск досягають якогось критичного значення, відбувається конденсація газу, тобто газ перетворюється в рідину.

У 1873 році голландський фізик Ян Дидерик ван дер Ваальс вивів рівняння стану реального газу, в якому врахував обсяг молекул а також сили відштовхування на малих відстанях та тяжіння на великих,

[p + n_М²·a/V²](V – n_М·b) = n_М·R·T,

де n_М – число молів, n_М = V/V_М, V_М [м³/моль] – об’єм 1 моля газу, V [м³] – об’єм газу.

Із цього рівняння можна розрахувати тиск p [Па = Н/м²] реального газу,

p = n_М·R·T/(V – n_М·b) – (n_М²·a/V²).

Критичні значення тиску p_CR [Н/м²] та температури Т_CR [К] у рівнянні ван дер Ваальса розраховуються по формулам

p_CR = a/(27·b²);

Т_CR = 8·a/(27·R·b).

Для критичних значень температури Т_CR = 126 К та тиску р_CR газу сталі a та b описуються виразами

b = R·Т_CR/(8·p_CR) [Н·м⁴/моль²];

a = 27·b²·p_CR [м³/моль].

Критичний молярний об’єм газу V_CR [м³/моль] для критичної температури Т_CR [Т] та критичного тиску p_CR [Па] розраховується по формулі

V_CR = 3·b = 3·R·Т_CR/(8·p_CR),

де b = R·Т_CR/(8·p_CR) [Н·м⁴/моль²].

Концентрація n_CR молекул газу в критичному стані більше концентрації молекул у нормальних умовах n₀,

n_CR/n₀ = р_CR·Т/(p·Т_CR)

або

n_CR/n₀ = Т·R/(8·p·b).

Відносна похибка при розрахунку тиску по рівнянням Клапейрона p₁ [Па] та ван дер Ваальса p₂ [Па] для об’єму V [м³] знаходиться наступним чином.

З рівняння Клапейрона вичислюємо тиск p₁ [Па],

p₁ = n_М·R·T/V.

З рівняння ван дер Ваальса визначаємо тиск p₂ [Па],

р₂ = n_М·R·T/(V – n_М·b) – (n_М²·a/V²).

Відносна похибка ε в розрахунках тиску по рівнянням Клапейрона та ван дер Ваальса складає

ε = (p₁ – р₂)/р₂.

Вичислюємо похибку в розрахунках повної внутрішньої енергії у разі, коли газ буде розглядатися як ідеальний для об’єму V [м³].

Внутрішня енергія ідеального газу U₁ [Дж]

U₁ = n_М·С_НV·T = n_М·(5/2)·R·T,

де С_НV – теплоємність при постійному об’ємі, С_НV = (i/2)·R = (5/2)·R, i = 5,

Внутрішня енергія реального газу U₂ [Дж]

U₂ = n_М·(С_НV·T – а/V_m) = n_М·[(5/2)·R·T – а/V_М].

Похибка ε в розрахунках повної внутрішньої енергії ідеального U₁ та реального U₂ газів знаходиться як відношення (U₁ – U₂)/U₂,

ε = (U₁ – U₂)/U₂ = 2·а/(5·V_M·R·T).

де V_M [м³/моль] – молярний об’єм, V_M = V/n_М.

Рівняння ван дер Ваальса описує збільшення тиску при зменшенні об'єму розріджених газів. Воно також визначає критичну температуру, вище якої газ не зріджується при жодному тиску. Поправки a і b мають більше значення при високих тисках газів. Для азоту, наприклад, при тиску 80 атм розрахунки, які проведені за рівняннями ідеального та реального газів, різняться приблизно на 5 %, а при тиску 400 атм різниця складає 100 %.

Енергетичні параметри газової повітряної суміші

Над рівнем моря пари води складають приблизно 1 % повітря. Більша частина маси атмосфери (~ 80 %) зосереджена в приземному шарі – тропосфері, яка простирається від рівня моря до висоти 12 кілометрів, з цієї відмітки починається інший шар – стратосфера.

При температурі 0 ⁰С та тиску повітря в 101325 Па маса 1 м³ повітря складає ~ 1,2928 кг. Розрахунковий вміст газів у повітряній суміші відповідає такому співвідношенню: азот N₂ – 78,08 %; оксиген О₂ – 20,95 %; вуглекислий газ CO₂ – 0,03 %; гідроген Н₂ та інертні гази – 0,94 %.

При нормальних атмосферних макропараметрах середня швидкість молекул оксигену О₂ у повітрі приблизно складає 480 м·с^–1, швидкість молекул азоту N₂ – 510 м·с^–1.

Пара води займає об’єм у 1700 раз більший, ніж у рідинному стані при тиску 1 атмосфера та температурі 100 ⁰С. Рідини газу випаровуються при температурі навіть нижче точки кипіння. Це явище зветься волатильністю рідини. В одному об’ємі разом наявні рідинна та парова фази, й перебувають вони при даному тиску в стані термодинамічної рівноваги

Користуючись наведеними формулами, можна визначити питомі фізико-хімічні та термодинамічні параметри газової повітряної суміші об’ємом 1 м³ при температурі 0 ⁰С та тиску повітря в 101325 Па, де 1 м³ повітря складає m = 1,2928 кг, а розрахунковий вміст азоту N₂ та оксигену О₂ у повітряній суміші дорівнює відповідно 78,08 % та 20,95 %.

1. Маса оксигену m(О₂) в повітряній суміші об’ємом 1 м³

m(О₂) = 0,2095·m = 0,2095·1,2928 кг = 0,2708 кг.

2. Маса азоту m(N₂) в повітряній суміші об’ємом 1 м³

m(N₂) = 0,7808·m = 0,7808·1,2928 кг = 1,0094 кг.

3. Разом вміст азоту та оксигену в повітрі перевищує 99 %.

4. Із рівняння Клапейрона (8.18) вичислюємо об’єм V(О₂), який займає оксиген,

V(О₂) = m(О₂)·R·T/(p·M) =

= 0,2708 кг·8,3155·[Дж/(моль·К)]·273 К/(101325 Па·32·10^–3 кг·моль^–1) = 0,1896 м³.

5. Із рівняння Клапейрона визначаємо об’єм V(N₂), який займає азот,

V(N₂) = m(N₂)·R·T/(p·M) =

= 1,0094 кг·8,3155·[Дж/(моль·К)]·273 К/(101325 Па·28·10^–3 кг·моль^–1) = 0,8077 м³. 6. Сумарний об’єм V(О₂ + N₂), який займають азот та оксиген,

V(О₂ + N₂) = V(N₂) + V(О₂) =

= 0,8077 м³ + 0,1896 м³ = 0,9973 м³

7. Кількість речовини оксигену n_М(О₂) в суміші

n_М(О₂) = ω(О₂)·m/M(О₂) =

= 0,2095·1,2928 кг/32·10^–3 кг/моль = 8,46 моль.

8. Кількість речовини азоту n_М(N₂) в суміші

n_М(N₂) = ω(N₂)·m/M(N₂) =

= 0,7808·1,2928 кг/28·10^–3 кг/моль = 36,05 моль.

9. Кількість речовини азоту та оксигену n_М(О₂ + N₂) в суміші

n_М(О₂ + N₂) = n_М(О₂) + n_М(N₂) = [m(О₂)/M(О₂)] + [m(N₂)/M(N₂)] = 44,51 моль.

10. Знайдемо енергію, якою володіють молекули оксигену U_ІD(О₂), коли його розглядають як ідеальний газ,

U_ІD(О₂) = [m(О₂)/M(О₂)]·С_HV·T= [m(О₂)/M(О₂)]·(5/2)·R·T =

= (0,2708 кг/32·10^–3 кг·моль^–1)·(5/2)·8,3155 [Дж/(моль·К)]·273 К = 48,027 кДж.

11. Знайдемо енергію, якою володіють молекули азоту U_ІD(N₂), коли його розглядають як ідеальний газ,

U_ІD(N₂) = [m(N₂)/M(N₂)]·С_HV·T = [m(N₂)/M(N₂)]·(5/2)·R·T =

= (1,0094 кг/28·10^–3 кг·моль^–1)·(5/2)· 8,3155 [Дж/(моль·К)]·273 К =

= 204,586 кДж.

12. Сумарна енергія, якою володіють оксиген та азот у суміші повітря, коли їх розглядають як ідеальні гази,

U_ІD(О₂ + N₂) = U_ІD(N₂) + U_ІD(О₂) =

= 204,586 кДж + 48,027 кДж = 252,613 кДж.

13. Енергія, якою володіють молекули оксигену U_R(О₂), коли його розглядають як реальний газ (8.70), враховуючи, що для оксигену a = 0,136 Н·м⁴/моль², b = 3,17·10^–5 м³/моль, критичні значення температури Т_CR = 152 К та тиску p_CR = 5 МПа, молярний об’єм V_M = V/n_М, V(О₂) = 0,1896 м³,

U_R(О₂) = [(m(О₂)/M(О₂)]·[(i/2)·R·T – а/V_M(О₂)] =

= (0,2708 кг/32·10^–3 кг·моль^–1)·{(5/2)·8,3155 Дж·моль^–1·К^–1·273 К –

– 0,136 (Н·м⁴/моль²)/[0,1896 м³/8,46 моль]} = 47,976 кДж.

14. Енергія, якою володіють молекули азоту U_R(N₂), коли його розглядають як реальний газ, враховуючи, що для азоту a = 0,136 Н·м⁴/моль²; b = 3,86·10^–5 м³/моль², критичні значення температури Т_CR = 126 К та тиску р_CR = 3,30 МПа, молярний об’єм V_M = V/n_М, V(N₂) = 0,8077 м³,

U_R(N₂) = [(m(N₂)/M(N₂)]·[(i/2)·R·T – а/V_M(N₂)] =

= (1,0094 кг/28·10^–3 кг·моль^–1){(5/2)·8,3155 Дж·моль^–1·К^–1·273 К –

– 0,136 Н·м⁴/моль²/[0,8077 м³/36,05 моль]} = 204,377 кДж.

15. Сумарна енергія, якою володіють оксиген та азот у суміші повітря, коли їх розглядають як реальні гази,

U_R(О₂ + N₂) = U_R(О₂) + U_R(N₂) =

= 47,976 кДж + 204,377 кДж = 252,353 кДж.

16. Похибка ε у визначенні енергії в двох випадках складає

ε = (U₁ – U₂)/U₂ =

= (252,613 – 252,353)/252,353 = 1,03·10^–3.

17. Відносна молекулярна маса повітря M(N₂ + О₂) може бути визначена через масові долі оксигену ω(О₂) та азоту ω(N₂), з яких в основному складається сухе повітря,

M(О₂ + N₂) = [ω(О₂) + ω(N₂)]/{[ω(О₂)/M(О₂)] + [ω(N₂)/M(N₂)]}=

= (0,2095 + 0,7808)/[(0,2095/32·10^–3) + (0,7808/28·10^–3)] =

= 29,04·10^–3 (кг/моль).

18. Тиск газової суміші повітря р [Па] складається із суми парціальних тисків р₁ [Па] та р₂ [Па],

р = р₁ + р₂ = ω₁·m·R·T/(M₁·V) + (1 – ω₁)·m·R·T/(M₂·V) =

= (R·T/V)·{(ω₁·m/M₁) + [(1 – ω₁)·m/M₂]} [Па].

19. Середнє значення повної кінетичної енергії однієї молекули оксигену E(О₂) при температурі 273 К та кількості вільностей і = 5 вичислюється по формулі,

E(О₂) = (5/2)·k_B·T =

= (5/2)·1,380622·10^–23 (Дж/К)·273 К = 0,94·10^–20 Дж.

20. При нормальних атмосферних макропараметрах середня швидкість молекул оксигену О₂ в повітрі приблизно складає 480 м·с^–1, швидкість молекул азоту N₂ – 510 м·с^–1. Молекули оксигену O₂ мають ту ж середню квадратичну швидкість ‹v_S1› = 790 м/с) при температурі T₁ = 1600 K, що й молекули гідрогену H₂ при температурі T₂ = 100 К,

T₁ = T₂·M₂/M₁ = 1600 K.

21. Температура газу T [К], при якій молекули оксигену досягнуть певної середньої квадратичної швидкості, наприклад, ‹v_S1› = 1000 м/с, розраховується із формули,

T = ‹v_S1›²·M/(3R) =

= (1000 м·с^–1)²·32·10^–3 кг·моль^–1/3·8,3155 Дж·моль^–1·К^–1 = 1283 К.

22. Визначимо середню квадратичну швидкість ‹v_S1› молекули оксигену при охолодженні газу до температури T = 223 К,

‹v_S1› = √(3·R·T/M) =

= √ [3·8,3155 Дж·моль^–1·К^–1·223 К/32·10^–3кг·моль^–1] = 417 м/с.

22. Знайдемо зміну внутрішньої енергії повітряної суміші, яка маючи об’єм V = 1 м³ при нормальному тиску p₁ = 101325 Па та нормальній температурі T₁ = 273 K, була охолоджена на ΔT = 50 К. Встановимо також кількість відданого нею тепла.

22.1. Із рівняння Клапейрона розраховуємо кількість молів речовини n_М [моль] в об’ємі 1 м³,

n_М = p₁·V/(R·T₁) =

= 101325 Па·1 м³/{8,3155 Дж·моль^–1·К^–1·273 K} = 44,634 моль.

22.2. Зміна внутрішньої енергії газу ΔU [Дж] складає

ΔU = (5/2)·n_М·R·ΔT =

= (5/2)·44,634 моль·8,3155 Дж·моль^–1·К^–1·50 К = 46394 Дж.

22.3. Згідно першому закону термодинаміки, кількість відданого тепла Q_Н [Дж] дорівнює зміні енергії ΔU [Дж],

Q_Н = ΔU = –46394 Дж.

22.4. Кількості тепла, яке витрачається для нагріву газу на ΔT [К] при постійному об’ємі Q_НV (ізохорний процес) та при постійному тиску Q_НP (ізобарний процес), відрізняються, і для оксигену становлять

Q_НV = (m/M)·C_НV·ΔT = (m/M)·(5/2)·R·ΔT;

Q_НP = (m/M)·C_НP·ΔT = (m/M)·(7/2)·R·ΔT.

де C_НV та C_НP – молярні теплоємності при постійному об’ємі (ізохорний процес) та при постійному тиску (ізобарний процес), для двоатомних молекул C_НV = (5/2)·R; C_НP = (7/2)·R.

Для порівняння, кінетична енергія потоку повітря, яке рухається зі швидкостями 1 м/с, 5 м/с та 10 м/с і падає на площу поперечного перетину А = 1 м² за 1 с, складає відповідно

E_WD1 = m_WD1·v²_WD1/2 = 1,2928 кг·1² (м/с)²/2 = 0,6464 Дж;

E_WD2 = m_WD2·v²_WD2/2 = 1,2928 кг·5·5² (м/с)²/2 = 80,8 Дж;

E_WD3 = m_WD3·v²_WD3/2 = 1,2928 кг·10·10² (м/с)²/2 = 646,4 Дж.

Тож, резерви внутрішньої енергії газового повітряного середовища значно перевищують рівні енергії вітру, які доступні для освоєння макроскопічними вітроенергетичними технологіями.

Узагальнена схема молекулярної вітроенергетичної системи

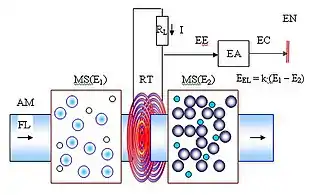
Узагальнена схема молекулярної системи вітроенергетики.

Узагальнена структурно-функціональна схема молекулярної системи вітроенергетики визначає функціональні частини, їх взаємозв'язки та призначення а також пояснює зміст та алгоритм енергетичних перетворень, що протікають в технологічному процесі виробництва електричного струму.

Молекулярна система вітроенергетики включає потік молекул повітря AM, газову повітряну суміш MS в енергетичних станах Е₁ [Дж] і Е₂ [Дж], приймач-перетворювач енергії RT, зовнішнє електричне навантаження R_L [Ом] та електричний адаптер EA.

Молекулярною газовою сумішшю MS слугує певний об’єм швидких молекул повітря. Різниця енергій ∆E [Дж] початкового E₁ та кінцевого E₂ станів молекулярної суміші відповідає енергії, що сприймається приймачем-перетворювачем RT й трансформується в електричну енергію E_EL [Дж] з певними втратами,

E_EL = k·∆E = k·(E₁ – E₂).

де k – коефіцієнт корисної дії приймача-перетворювача, в загальному випадку цей коефіцієнт залежить від багатьох факторів і є добутком коефіцієнтів корисної дії складових елементів k₁, k₂, k₃,…k_N, які задіяні послідовно в процесі енергетичних перетворень, k = k₁·k₂·k₃·…·k_N.

Для ефективного перетворення енергії швидких молекул газової повітряної суміші в електричну енергію можна використати явище ступінчато-ударної йонізації атомів та молекул активної речовини під дією швидких молекул повітря, термоелектричний ефект Зеебека – виникнення термо-ЕРС в молекулярній структурі під тепловою дією швидких молекул повітря, сорбційний ефект – виникнення термо-ЕРС у сорбційній молекулярній структурі при поглинанні швидких молекул повітря, прямий п’єзоелектричний ефект – виникнення електричних зарядів на гранях певних кристалів при їх деформації та зворотний магнітострикційний ефект (магнетопружний ефект Вілларі) – зміна намагніченості певних матеріалів під впливом механічних напружень тощо.

Джерелом відновлюваної енергії слугує кінетична енергія швидких молекул повітря та вітер, який періодично поновлює кожен наступний об’єм швидких молекул повітря на заміну тим, у яких енергія відібрана.

Молекулярна вітроенергетична система функціонує так. Кінетична енергія швидких молекул повітря KN у приймачі-перетворювачі RT трансформується в електричну енергію ЕE (енергію електричного струму ЕС). Параметри електричного струму (електрична напруга u, сила струму і та частота f) доводяться в електричному адаптері ЕА до стандартних значень, і струм спрямовується споживачам та/або в електричну мережу ЕN.

За фізичними принципами отримання електричного струму молекулярні системи вітроенергетики можна класифікувати на йонізаційні, вітрильні, п’єзоелектричні, магнітострикційні та інші.

Схеми, конструкції, параметри та характеристики систем молекулярної вітроенергетики досліджуються в рамках молекулярної фізики, молекулярної кінетики газів, фізики та хімії поверхні, молекулярної аеромеханіки, термодинаміки та електродинаміки.

Йонізаційні системи молекулярної вітроенергетики

Принцип дії

Принцип дії йонізаційної молекулярної системи вітроенергетики заснований на йонізації активної структури швидкими молекулами повітря та використанні вільних зарядів для виробництва електричного струму.

Чисельно енергія йонізації дорівнює йонізаційному потенціалу або ширині забороненої зони речовини приймача-перетворювача. Перетворення енергії швидких молекул повітря в електричну енергію може бути виконано бомбардуванням молекулами активної структури. Оскільки кінетичної енергії одиночного удару молекули повітря недостатньо для йонізації атома активної речовини, використовується механізм ступінчато-ударної йонізації. У цьому випадку атоми чи молекули активної речовини за рахунок первинних ударів швидких молекул повітря переводяться в збуджений стан. Після цього для їх йонізації достатньо подіяти на них з енергією, рівною різниці енергії йонізації та енергії збудження. Подібна ступінчато-ударна йонізація можлива за умов, якщо частинка активної речовини у проміжок часу між двома зіткненнями перебуває в метастабільному стані та не встигає загубити енергію, отриману при першому зіткненні. Під дією енергії йонізації електрон переходить із валентної зони в зону провідності, а нейтральний атом твердого тіла перетворюється в заряджений йон.

Віддаючи енергію, молекулярна система повітряної газової суміші охолоджується, і тиск газу знижується. При низьких критичних температурах рух молекул повітря цілком припиняється, тиск газу зникає, частина молекул повітря навіть конденсується.

Схеми йонізаційних молекулярних систем

Основними компонентами вітроенергетичного пристрою для виробництва електричного струму шляхом ступінчато-ударної йонізації є молекулярна система енергії MS, йонізаційний приймач-перетворювач CPIN та електричний адаптер EA.

Молекулярною системою енергії MS слугує певний об’єм швидких молекул повітря.

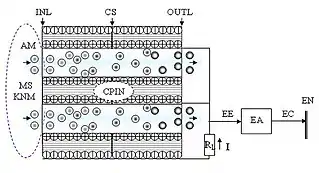
Вітроенергетичний пристрій для виробництва електричного струму шляхом ступінчато-ударної йонізації.

Для досягнення високої енергетичної ефективності йонізаційний перетворювач повинен мати велику площу дотику активної поверхні та швидких молекул повітря. Цій умові відповідає приймач-перетворювач CPIN, виконаний у вигляді капілярної структури CS з вхідними INL та вихідними OUTL отворами. Можливо, першими, хто зрозумів переваги використання капілярних систем у роботі з газами були англійські фізики Джеймс Прескотт Джоуль та Вільям Томсон лорд Кельвін. Працюючи разом продовж 1852-1862 рр., вони відкрили ефект незалежності внутрішньої енергії газу від об’єму.

Йонізаційна структура конструктивно може бути виконана у вигляді тонких регулярних циліндричних трубок СPT радіусом r_CP [м] і довжиною L_CP [м]. Капілярній системі властиві повторюваність структури. Коефіцієнт корисної дії йонізаційного перетворювача є відношенням величини виробленої електричної енергії до витрат внутрішньої енергії повітряної суміші.

Робота пристрою протікає так. При попаданні повітря в приймач-перетворювач CPIN швидкі молекули повітря AM бомбардують активну структуру. У результаті бомбардування частина нейтральних молекул приймача-перетворювача йонізуються. На його електродах формується стрибок потенціалу, і в замкнутому електричному контурі через електричний навантажувальний опір R_L [Ом] протікає електричний струм I [А]. В електричному адаптері EA цей постійний електричний струм перетворюється в змінний. Його параметри доводяться до стандартів, придатних для використання, й він спрямовується споживачам та/або в електричну мережу ЕN.

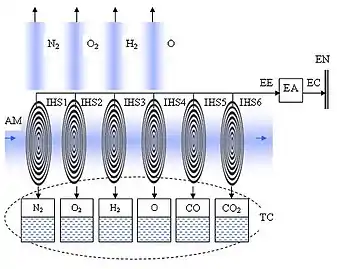
Вітроенергетична система на основі йонізаційного гетероструктурного перетворювача.

З метою підвищення потужності енергогенеруючої системи площу активної поверхні йонізаційної структури збільшують, утворюючи гетероструктурні йонізаційні елементи IHSN – молекулярні матриці, з’єднані між собою паралельно–послідовно.

Схема каскадної йонізаційної вітроенергетичної системи складається із йонізаційного гетероструктурного перетворювача, теплорегулюючої секції ТC та електричного адаптера EA.

Йонізаційний гетероструктурний перетворювач включає ряд гетероструктурних йонізаційних елементів (молекулярних матриць) IHS1, IHS2, IHS3, IHS4, IHS5 IHS6.

Теплорегулююча секція виконує теплообмінну функцію, використовуючи теплообмінники з потоком рідини FL, які працюють синхронно з капілярною йонізаційною структурою.

Параметри молекулярної вітроенергетичної системи визначаються в рамках кінетичної теорії газів.

Енергетичні та економічні параметри

Головними технічними та економічними показниками йонізаційної енергогенеруючої системи є фізико-хімічні та термодинамічні параметри повітряної суміші об’ємом 1 м³, загальний об’єм молекулярної повітряної суміші V_MS [м³], об’ємні витрати повітря Q_AIR [м³/с], коефіцієнт корисної дії k_W (коефіцієнт відбору внутрішньої кінетичної енергії молекулярної системи), електрична потужність P_EL [Вт], річний виробіток електроенергії Е_EL [кВт·год], вартість річного виробітку електричної енергії P_PRΣ [US$], обсяг викопного органічного палива, наприклад, об’єм V_OFF [м³] природного газу з питомою теплотворною здатністю с_OFF [Дж/м³], який заощаджується при функціонуванні молекулярної системи продовж року.

З урахуванням величини питомих фізико-хімічних та термодинамічних параметрів газової повітряної суміші об’ємом 1 м³ при температурі 0 ⁰С та тиску повітря в 101325 Па, визначених раніше (8.81)-(8.106), тепер час повернутися до звичних традицій оцінки молекулярної системи енергетики в рамках усталених енергетичних та економічних параметрів та характеристик, корисних для побудови та експлуатації молекулярної вітроенергетичної системи, бо що стосується споживання, ми всі – невиправні консерватори.

Коефіцієнт корисної дії вітрової молекулярної системи k_WD характеризує ефективність і визначається відношенням виробленої електричної енергії E_EL [Дж] до енергії молекулярної системи E_MS [Дж], яка була затрачена на виробництво енергії,

k_WD = E_EL/U_MS.

Коефіцієнт корисної дії молекулярної системи характеризує ефективність йонізаційного перетворювача кінетичної енергії швидких молекул повітря в електричну енергію.

Електрична потужність молекулярної системи P_EL [Вт] визначає кількість електричної енергії, яка може бути вироблена в одиницю часу,

P_EL = ∆E_EL/∆t = ∆V·k_WD·U_MS/∆t = k_WD·U_MS·(∆V/∆t) =

= k_WD·U_MS·Q_AIR [Вт],

де ∆E_EL [Дж] – обсяг електричної енергії, який виробляє система продовж певного часу ∆t [с]; U_MS [Дж] – внутрішня кінетична енергія молекул газової повітряної суміші об’ємом 1 м³, U_MS = U_ІD(О₂ + N₂) [Вт·с/м³], k_WD – коефіцієнт корисної дії молекулярної системи, Q_AIR [м³/с] – об’ємні витрати повітря, тобто об’єм повітря V [м³], який витрачається молекулярною системою в одиницю часу, Q_AIR = ∆V/∆t [м³/с].

Потужність швидких молекул повітря, які находяться в 1 м³ молекулярної газової суміші,

P_EL = k_WD·{[m(О₂)/M(О₂)] + [m(N₂)/M(N₂)]}·Q_AIR·(5/2)·R·T.

Обсяг електроенергії Е_EL [Дж], яка може бути вироблена за певний час роботи системи, наприклад, продовж року, дорівнює добутку її електричної потужності P_EL [Вт] на час роботи t [с],

Е_EL = P_EL·t =

= k_WD·{[m(О₂)/M(О₂)] + [m(N₂)/M(N₂)]}·Q_AIR·(5/2)·R·T·t [Дж].

Вартість електричної енергії P_PRΣ [US$], яка може бути вироблена за певний період роботи системи, наприклад, продовж року, дорівнює добутку ціни одиниці електричної енергії p_PR [US$/кВт·год] на обсяг електроенергії Е_EL [кВт·год] ,

P_PRΣ = p_PR·Е_EL =

= p_PR·k_WD·{[m(О₂)/M(О₂)] + [m(N₂)/M(N₂)]·Q_AIR·(5/2)·R·T·t [US$].

Кількість викопного органічного палива, наприклад, об’єм V_OFF [м³] природного газу з питомою теплотворною здатністю с_OFF [Дж/м³], який заощаджується при функціонуванні молекулярної системи продовж року, розраховується так

V_OFF = Е_EL/(k_OFF·с_OFF) =

= k_WD·{[m(О₂)/M(О₂)] + [m(N₂)/M(N₂)]}·Q_AIR·(5/2)·R·T·t/(k_OFF·с_OFF) [м³],

де k_OFF – коефіцієнт корисної дії теплоенергетичних систем на органічному паливі, в енергоефективних системах k_OFF = 0,4.

Вітрильні молекулярні системи виробництва електричного струму

Принцип роботи вітрильних молекулярних систем

Принцип роботи вітрильних молекулярних систем заснований на виникненні спрямованого руху твердотільної частинки з анізотропними властивостями поверхні в ізотропному середовищі швидких молекул повітря.

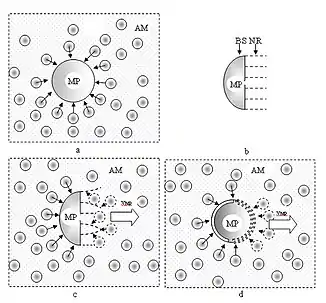
Дія швидких молекул повітря на сферичну мікрочастинку з анізотропними властивостями поверхні та виникнення її вітрильного спрямованого руху у повітряному середовищі.

Подібно тому, як ведуть себе молекули рідини з молекулами поверхні твердого тіла в гідродинаміці, молекули повітряної суміші по відношенню до поверхні твердого тіла також можуть бути фізично (хімічно) активними або ж неактивними. У першому випадку молекули газу активно взаємодіють з молекулами твердого тіла, й така поверхня є аерофільною. У разі, коли молекули газів повітряної суміші є фізично (хімічно) неактивними по відношенню до поверхні твердого тіла, вони слабко взаємодіють з нею, така поверхня є аерофобною. Технології шліфування, полірування, хонінгування, електроерозійної обробки, літографії, хімічного травлення, лазерного текстурування окремо і в сукупності дають змогу фрагментарно структурувати поверхню та досягати її анізотропних властивостей по відношенню до оточуючого повітряного середовища. Тож, з’являється можливість контролювати рух мікрочастинок різної форми та фізико-хімічного складу в повітряному середовищі (ефект вітрила) і на їх основі створювати ефективні молекулярні електродинамічні системи виробництва електричного струму. Основу електродинамічного генеруючого пристрою вітрильного типу можуть складати мікроскопічні мобільні магніти, частина поверхні яких модифікована та має відмінні властивості по відношенню до швидких молекул повітря.

Середня квадратична швидкість ‹v_MPS› мікроскопічної частинки визначається по формулі ‹v_MPS› = √(3·k_B·T/m_MP),

де m_MP [кг] – маса частинки, k_B [Дж/К] – стала Больцмана, k_B = R/N_A = 1,380622·10^–23 Дж/К, T [К] – температура.

Натомість, середня квадратична швидкість молекули однорідного газу ‹v_S›

‹v_S› = √ (3·R·T/M),

де M [кг/моль] – молярна маса однорідного газу, R [Дж/(К·моль)] – універсальна газова стала, R = 8,3144 Дж/(К·моль).

Середня квадратична швидкість молекули однорідного газу ‹v_S› [м/с] перевищує середню квадратичну швидкість мікроскопічної частинки ‹v_MPS› [м/с],

‹v_S›/‹v_MPS› = √(3·R·T/M)/√(3·k_B·T/m_MP) = √(N_А·m_MP/M),

де N_А – число Авагадро, N_А = 6,02214·10²³ моль⁻¹.

Наприклад, якщо мікроскопічна частинка MP масою m_MP = 1·10⁻¹¹ кг перебуває в газовому оксигені О₂, розрахунковий вміст якого в повітряній суміші складає близько 20,95 %, то середні квадратичні швидкості молекули однорідного газу ‹v_S› та мікроскопічної частинки ‹v_MPS› відносяться як

‹v_S›/‹v_MPS› = √[N_А·m_MP/M] =

= √[6,022141·10²³ моль⁻¹·1·10⁻¹¹ кг/(32·10⁻³ кг·моль⁻¹)] = 1,37·10⁷.

Тож, середня квадратична швидкість мікроскопічної частинки дуже мала. Воно й не дивно, якщо врахувати, що маса окремої молекули оксигену m(О₂) складає

m(О₂) = М/N_A =

= 32·10^–3 кг·моль⁻¹/6,022141·10²³ моль⁻¹ = 5,31·10^–26 кг.

де М [кг·моль⁻¹] – молярна маса оксигену, М = 32·10^–3 кг·моль⁻¹.

Тепер уявімо собі мікроскопічну частинку, половина якої виготовлена з особливої речовини, цей фрагмент має специфічну структуру поверхні, тож, володіє відмінними властивостями, порівнюючи з іншою половиною поверхні, й характерним чином взаємодіє зі швидкими молекулами оточуючого повітряного середовища. Якщо таку мікрочастинку з анізотропними властивостями поверхні занурено в повітряне середовище, швидкі молекули повітря бомбардуватимуть її та спричинятимуть тиск на її поверхню. Величина тиску визначається кількістю зіткнень молекул з поверхнею тіла. Сила F, яка діє на занурене в повітря тіло при постійному тиску р [Па], пропорційна площі поверхні А [м²].

Порівняна швидкість вітру v [м/с], яка спричиняє на мікрочастинку той же ефект, що і швидкі молекули повітря,

v = √[p/(2·ρ)] =

= √[101325 Па/(2·1,2928 кг/м³)] = 200 м/с.

Тож, швидкість вітру мала б становити 200 м/с.

Зменшення ефективної площі поверхні та збільшення різниці сил F₁ – F₂, спрямованих назустріч одна одній, може бути досягнуто, наприклад, структуруванням поверхні.

Виникнення спрямованого руху твердотільної частинки з анізотропними властивостями поверхні в ізотропному середовищі швидких молекул повітря віддалено нагадує ефект вітрила. Вітрило – засіб, який використовує енергію вітру для пересування морського, наземного чи іншого виду транспорту. У древні роки вітрильні судна йшли повільно й переважно в одному напрямі – за вітром. Відсутність вітру в ізотропному повітряному середовищі не є перешкодою для спрямованого руху мікрочастинки з анізотропними властивостями поверхні. Описаний принцип «вітрила» можна застосувати, аби рухати мікрочастинки різної форми, зокрема, сферичної і на їх основі створювати ефективні електродинамічні системи виробництва електричного струму.

Електродинамічний генеруючий пристрій вітрильного типу

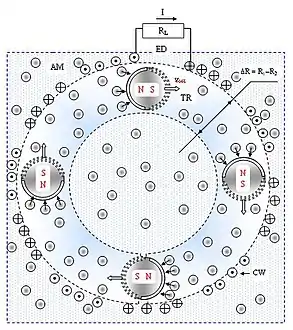
Вітрильний електродинамічний пристрій.

Схема електродинамічного генеруючого пристрою вітрильного типу включає електродинамічний кільцеподібний перетворювач EDR, який включає провідникову обмотку CW та кілька мікроскопічних мобільних магнітів MT, встановлених у підвісі на рівних відстанях один від одного. Магніти врівноважені в середовищі молекул повітря AM. Половина поверхні кожного магніту модифікована та має відмінні властивості по відношенню до швидких молекул повітря. Положення структурованої поверхні узгоджене з напрямком силових ліній магнітного поля S-N, так що мікроскопічні магніти рухаються один за одним по кільцевій траєкторії TR. Ширина кільця ΔR [м] визначається різницею зовнішнього R₁ [м] та внутрішнього R₂ [м] радіусів траєкторії

ΔR = R₁ – R₂ [м].

Електродинамічний пристрій вітрильного типу функціонує так. Швидкі молекули повітря приводять в рух магніти й «транспортують» їх по кільцевій траєкторії відносно провідникової обмотки CW. Силові лінії рухомого магнітного поля перетинають площину провідникової обмотки й відповідно закону електромагнітної індукції Майкла Фарадея індукують у ній електричний струм. Напрям наведеного струму (позначений символом «+», від спостерігача) в різних частинах обмотки однаковий, бо однаковим є напрям руху та положення силових ліній поля кожного магніту відносно провідника. У результаті, електричні струми I₁, I₂,…І_N [А], які індуковані кожним магнітом, складуються. Сумарна сила струму I_Σ [А] вираховується таким чином

I_Σ = I₁ + I₂ + … І_N = I_i·N [А],

де N – число магнітів.

З обмотки сумарний електричний струм поступає в зовнішній контур електричного навантажувального опору R_L [Ом].

Примітки

Сидоров, В.І. (2018). Від макроскопічних до молекулярних технологій відновлюваної енергії.. Промислова електроенергетика та електротехніка – № 3. – С. 34-42 (Укр.).
Сидоров, В.І. (2020). Молекулярна енергетика. Теорія та технічні рішення (Укр.). Черкаси: Вертикаль, видавець Кандич С.Г. с. 486. ISBN ISBN 978-617-7475-79-7.
Clapeyron, E. (1834). Mémoire sur la puissance motrice de la chaleur. Journal de l'École Polytechnique. – XIV. – Р. 153-90 (Фр.).
Mayer, J. R. (1867)). Die Mechanik der Wärme (Нім.). с. 294.
Waterston, J. J. (1843). Thoughts on the Mental Functions.
Krönig, A. (1856). Grundzüge einer Theorie der Gase. Annalen der Physik. – Vol. 99 (10): – Р. 315-322 (Нім.).
Clausius, R. (1850). Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen. Annalen der Physik. – Vol. 79. – Р. 368-397, 500-524 (Нім.).
Clausius, R. (1857). Über die Art der Bewegung, die wir Wärme nennen. Annalen der Physik. – Vol. 100. – Р. 353-379 (Нім.).
Maxwell, J. C. (1867). On the Dynamical Theory of Gases. Philosophical Transactions of the Royal Society of London. – Vol. 157. – 49 (Англ.).

Джерела

Сидоров В.І. (2018). Від макроскопічних до молекулярних технологій відновлюваної енергії.Промислова електроенергетика та електротехніка – № 3. – С. 34-42 (Укр.).
Сидоров, В.І. (2020). Молекулярна енергетика. Теорія та технічні рішення (Укр.). Черкаси: Вертикаль, видавець Кандич С.Г. с. 486 с. ISBN ISBN 978-617-7475-79-7.
Boyle, R. (1674.). wo volumes of tracts on the Saltiness of the Sea, Suspicions about the Hidden Realities of the Air, Cold, Celestial Magnets.
Boyle, R. (1660.). New Experiments Physico-Mechanical: Touching the Spring of the Air and their Effects (Англ.). Oxford, H-Hall.
Boyle, R. A (1669). A Continuation of New Experiments Physico-mechanical, Touching the Spring and Weight of the Air, and Their Effects (Англ.). Oxford, H-Hall. с. 198.
Mariotte, E. (1679.). Essais de Physique, ou mémoires pour servir à la science des choses naturelles "Second essai. De la nature de l'air" (Фр.). Paris, France: E. Michallet.
Humboldt, A., Gay-Lussac, J. L. . (1804.). Mémoires sur l'analyse de l'air atmosphérique(Фр.). Paris.
Gay-Lussac, J. L. (1827-1828). Cours de physique (Фр.). Paris. с. 562 p.
Gay-Lussac, J. L. (1802). Recherches sur la dilatation des gaz et des vapeurs. Annales de chimie. – 43. – Р. 137-175. (Фр.).
Avogadrо, A. (1811). Essai d'une manière de déterminer les masses relatives des molécules élémentaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons.Journal de Physique, de Chimie et d'Histoire naturelle. – 73. – Р. 58-76. (Фр.).
Clapeyron, E. (1834). Mémoire sur la puissance motrice de la chaleur. Journal de l'École Polytechnique. – XIV. – Р. 153-90. (Фр.).
Mayer, J. R. (1867). Die Mechanik der Wärme (Нім.). с. 294 р.
Mayer, J. R. (1842). Bemerkungen über die Kräfte der unbelebten Natur. Annalen der Chemie und Pharmacie. – 42 (2). – Р. 233-240. (Нім.).
Waterston, J. J. (1843.). Thoughts on the Mental Functions (Англ.).
Krönig, A. (1856). Grundzüge einer Theorie der Gase. Annalen der Physik. – Vol. 99 (10): – Р. 315-322. (Нім.).
Clausius, R. (1850). Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen. Annalen der Physik. – Vol. 79. – Р. 368-397, 500-524. (Нім.).
Clausius, R. (1857). Über die Art der Bewegung, die wir Wärme nennen. Annalen der Physik. – Vol. 100. – Р. 353-379. (Нім.).
Maxwell, J. C. (1867). On the Dynamical Theory of Gases. Philosophical Transactions of the Royal Society of London. – Vol. 157. – 49 р. (Англ.).
Boltzmann, L. E. (1871). Analytischer Beweis des zweiten Haubtsatzes der mechanischen Wärmetheorie aus den Sätzen über das Gleichgewicht der lebendigen Kraft.
Boltzmann, L. E. (1871). Über das Wärmegleichgewicht zwischen mehratomigen Gasmolekülen.
Thomson, W. (1851). On the dynamical theory of heat; with numerical results deduced from Mr. Joule's equivalent of a thermal unit and M. Regnault's observations on steam. Math. and Phys. Papers. – Vol. 1. – Р. 175-183. (Англ.).
Van der Waals, J. D. (1873). Over de Continuiteit van den Gas- en Vloeistoftoestand (on the continuity of the gas and liquid state). PhD thesis (Нім.). Leiden, The Netherlands.
Einstein, A. (1905). Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten. Teilchen. Annalen der Physik. – Vol. 17 (8). – Р. 549-560. (Нім.).
Smoluchowski, M. (1906). Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. Annalen der Physik. – Vol. 21 (14). – Р. 756-780. (Нім.).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Сидоров, В.І. (2018). Від макроскопічних до молекулярних технологій відновлюваної енергії.. Промислова електроенергетика та електротехніка – № 3. – С. 34-42 (Укр.).

[2] Сидоров, В.І. (2020). Молекулярна енергетика. Теорія та технічні рішення (Укр.). Черкаси: Вертикаль, видавець Кандич С.Г. с. 486. ISBN ISBN 978-617-7475-79-7.

[3] Clapeyron, E. (1834). Mémoire sur la puissance motrice de la chaleur. Journal de l'École Polytechnique. – XIV. – Р. 153-90 (Фр.).

[4] Mayer, J. R. (1867)). Die Mechanik der Wärme (Нім.). с. 294.

[5] Waterston, J. J. (1843). Thoughts on the Mental Functions.

[6] Krönig, A. (1856). Grundzüge einer Theorie der Gase. Annalen der Physik. – Vol. 99 (10): – Р. 315-322 (Нім.).

[7] Clausius, R. (1850). Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen. Annalen der Physik. – Vol. 79. – Р. 368-397, 500-524 (Нім.).

[8] Clausius, R. (1857). Über die Art der Bewegung, die wir Wärme nennen. Annalen der Physik. – Vol. 100. – Р. 353-379 (Нім.).

[9] Maxwell, J. C. (1867). On the Dynamical Theory of Gases. Philosophical Transactions of the Royal Society of London. – Vol. 157. – 49 (Англ.).