Обернений оператор
Обернений оператор до оператора — оператор, який кожному із множини значень оператора ставить у відповідність єдиний елемент із області визначення оператора , який є розв'язком рівняння . Якщо оператор має обернений, тобто рівняння має єдиний розв'язок за будь-якого із , то називають оборотним. Обернений оператор позначають [1].
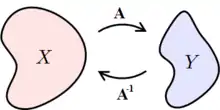
Визначення та умови існування
Інше визначення: оператор називають оберненим до оператора , якщо , де — одиничний оператор. Якщо виконується тільки співвідношення або тільки то оператор називають лівим оберненим або правим оберненим відповідно. Якщо оператор має лівий обернений і правий обернений, то вони рівні між собою, а оператор є оборотним[2]. Якщо обернений оператор існує, він визначається єдиним чином[3].
Оператор оборотний, якщо він відображає на взаємно однозначно, тобто за різних набуває різних значень [4]. Якщо оператор — лінійний, то для існування оберненого оператора достатньо, щоб виконувалося тільки при [5].
Лінійний оператор (навіть обмежений) може мати обернений, визначений не на всьому просторі. Наприклад, у просторі лінійний оператор
має обернений, який визначено для векторів із першою координатою рівною нулю: [5].
Властивості
- [6]
- [3]
- Оператор , обернений до лінійного оператора, також лінійний[1].
- , — спряжений оператор[7].
Теореми про обернений оператор
Теорема Банаха
|
Нехай — лінійний обмежений оператор, який взаємно однозначно відображає Банахів простір на Банахів простір . Тоді обернений оператор обмежений. |
Теорема Банаха є одним з основних принципів лінійного аналізу. З неї випливає теорема про відкрите відображення: лінійне неперервне відображення Банахового простору на (всі) Банахові простори відкрите[8].
Достатня умова існування оберненого оператора
- Нехай лінійний оператор , який відображає лінійний нормований простір на лінійний нормований простір , задовольняє для будь-якого умові
де — деяка константа. Тоді існує обернений обмежений лінійний оператор [9].
- Нехай — лінійний обмежений оборотний оператор, що діє з Банахового простору в Банахів простір і — лінійний обмежений оператор з в такий, що . Тоді оператор має обмежений обернений, причому
- Нехай — Банахів простір, — тотожний оператор в , а — такий лінійний обмежений оператор, який відображає в себе, що . Тоді оператор існує, обмежений і подається у вигляді ряду
- [12].
Приклади
Перетворення Фур'є
можна розглядати як лінійний обмежений оператор, що діє з простору в себе. Оберненим оператором для нього є обернене перетворення Фур'є
- [13].
Оператори інтегрування та диференціювання
Для оператора інтегрування
який діє в просторі неперервних функцій , оберненим буде оператор диференціювання:
визначений на лінійному многовиді неперервно диференційовних функцій, таких що [14].
Оператор Штурма — Ліувілля
Для диференціального оператора Штурма — Ліувілля
визначеного на лінійному многовиді двічі неперервно диференційовних функцій таких, що , оберненим оператором є інтегральний оператор
де — функція Гріна. — лінійний обмежений оператор у [14].
Інтегральний оператор
Нехай
— інтегральний оператор у просторі безперервних функцій . За достатньо малих значень параметра оператор (де — одиничний оператор) має обмежений обернений
- ,
де — резольвента ядра . Знаючи резольвенту, можна знайти розв'язок інтегрального рівняння
за будь-якого вільного члена [15].
Обернений оператор у скінченновимірному просторі
Оператор у скінченновимірному просторі оборотний тоді й лише тоді, коли його ранг збігається з розмірністю простору. Інакше кажучи, визначник його матриці відмінний від нуля. Оберненому оператору відповідає обернена матриця[16].
Див. також
Примітки
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 225.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 128.
- Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу, 1979, с. 168.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 351.
- Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу, 1979, с. 319.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 154.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 207.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, глава IV, §5, п. 4.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 155.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 157.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 229.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 230.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, глава VIII.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 161.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 163.
- Ильин В. А., Позняк Э. Г. Линейная алгебра. Учеб. для вузов. — 5-e изд. — М. : Физматлит, 2002. — 320 с. — ISBN 5-9221-0129-3.
Література
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 4-е изд. — Москва : Наука, 1976. — 544 с. — ISBN 5-9221-0266-4.(рос.)
- Люстерник Л. А., Соболев В. И.. Элементы функционального анализа. — Изд. 2-е, перераб. — М. : Наука, 1965. — 520 с.
- Рисс Ф., Сёкефальви-Надь Б.. Лекции по функциональному анализу. — М. : Мир, 1979. — 592 с.
- Соболев В. И. Обратное отображение // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1982. — Т. 3. — 592 с. — 150 000 экз.