Паралельне перенесення (диференціальна геометрія)

У геометрія паралельне перенесення — спосіб перенесення геометричних даних вздовж гладких кривих у многовиді. Якщо на многовиді задано афінну зв'язність (коваріантну похідну або зв'язність на дотичному просторі), то ця зв'язність дозволяє переносити дотичні вектори многовиду вздовж кривих, щоб вони залишалися «паралельними» відносно зв'язності.

Таким чином, паралельне перенесення для зв'язності дає спосіб, у певному сенсі, переносити локальну геометрію многовида уздовж кривої: тобто «з'єднувати» геометрії сусідніх точок. Загалом може існувати нескінченна кількість способів паралельного перенесення, але специфікація одного є рівнозначною заданню зв'язності. Фактично, звичайне поняттям зв'язності є інфінітезимальним аналогом паралельного перенесення. Навпаки, паралельне перенесення — локальна реалізація зв'язності.

Оскільки паралельне перенесення забезпечує локальну реалізацію зв'язності, воно також забезпечує локальну реалізацію кривини, відому як голономія. Теорема Емброуза — Сінгера явно задає таке співвідношення між кривиною та голономією.

Інші поняття зв'язності оснащені власними системами паралельного перенесення. Наприклад, зв'язність Кошуля у векторному розшаруванні також дозволяє паралельне перенесення векторів у значній мірі так само, як у випадку коваріантної похідної. Зв'язності Картана і Ересмана дозволяють ввести поняття «підняття кривих» з многовида на загальний простір головного чи локально тривіального розшарування.

Паралельне перенесення вздовж кривої на поверхні

Паралельне перенесення вектора по замкнутому контурі на сфері. Кут

\alpha

є пропорційним площі всередині контуру.

У звичайному тривимірному просторі $\mathbb {R} ^{3}$ дотичний простір у кожній точці можна ідентифікувати із самим простором $\mathbb {R} ^{3}$ . Для будь-якої регулярної кривої $\gamma \colon I\to \mathbb {R} ^{3}$ кожній точці $\gamma (t)$ кривої можна присвоїти вектор $X(t)\in \mathbb {R} ^{3}.$ Якщо при цьому $X(t)=const$ , то векторне поле $X(t)$ вздовж кривої називається паралельним. Очевидно, що $X(t)=const$ , тоді і тільки тоді, коли для похідної є правильною рівність ${\dot {X}}(t)=0.$

Якщо вектори зображати, як направлені відрізки із початком у точці кривої, то для паралельного векторного поля всі відрізки матимуть однакову довжину і будуть паралельними.

Паралельні векторні поля для площини

Для площини P у тривимірному просторі її дотичний простір теж можна ідентифікувати із самою площиною. Для кривої $\gamma \colon I\to P$ , якщо кожній точці $\gamma (t)$ кривої присвоїти вектор $X(t)\in \mathbb {R} ^{3}$ , що є паралельним площині P (тобто, його можна інтерпретувати як дотичний вектор у точці $\gamma (t)$ ), то у випадку диференційовності поля $X(t)$ поле ${\dot {X}}(t)$ теж буде складатися із дотичних векторів до площини у відповідних точках кривої. Зокрема полями, що задовольняють диференціальне рівняння ${\dot {X}}(t)=0$ теж будуть векторні поля $X(t)=const$ , де єдиним обмеженням у цьому випадку є те, що цей єдиний вектор є паралельний площині P. Такі поля теж називаються паралельними.

Паралельні векторні поля для довільної регулярної поверхні

Для загальної регулярної поверхні S у $\mathbb {R} ^{3}$ для регулярної кривої $\gamma \colon I\to S$ може не існувати поля $X(t)=const$ такого, що $X(t)\in T_{\gamma (t)}S$ . Також звичайна похідна (у тривимірному просторі) гладкого векторного поля може не бути векторним полем (тобто відповідні вектори не належатимуть дотичним площинам). У цьому випадку замість звичайної похідної векторного поля вздовж кривої має її тангенціальну складову, тобто проекцію похідної на дотичну площину. А саме для кривої $\gamma \colon I\to \mathbb {R} ^{3}$ , точки $p=\gamma (t_{0}),\;t_{0}\in I$ і диференційовного векторного поля $X(t)$ можна ввести коваріантну похідну:

\nabla _{{\dot {\gamma }}(t_{0})}X(t)=({\dot {X}}(t))(t_{0})-\langle ({\dot {X}}(t))(t_{0}),N(t_{0})\rangle N(t_{0})

де $N(t_{0})$ позначає нормаль до поверхні у даній точці.

Векторне поле $X(t)$ називається паралельним, якщо воно задовольняє рівнянню:

\nabla _{{\dot {\gamma }}(t)}X(t)=0.

Властивості

У локальних координатах, якщо записати $S=S(u,v),\;\gamma (t)=S(u(t),v(t)),\;X(\gamma (t))=X(t)=a(t)S_{u}+b(t)S_{v}$ то рівняння для паралельного поля вздовж кривої можна записати як лінійну систему диференціальних рівнянь другого порядку:

\nabla _{{\dot {\gamma }}(t)}X(t)=({\dot {a}}+\Gamma _{11}^{1}a{\dot {u}}+\Gamma _{12}^{1}a{\dot {v}}+\Gamma _{12}^{1}b{\dot {u}}+\Gamma _{22}^{1}b{\dot {v}})S_{u}+({\dot {b}}+\Gamma _{11}^{2}a{\dot {u}}+\Gamma _{12}^{2}a{\dot {v}}+\Gamma _{12}^{2}b{\dot {u}}+\Gamma _{22}^{2}b{\dot {v}})S_{v}=0.

де всі похідні беруться по t, а

\Gamma _{bc}^{a}

— символи Крістофеля.

Із властивостей лінійних диференціальних рівнянь випливає, що для довільного вектора $X\in T_{p}S,\;p=\gamma (t_{0}),$ існує єдине паралельне векторне поля вздовж кривої значення якого у точці p буде рівним X. Це поле називається паралельним перенесенням вектора X вздовж кривої. Зокрема для $s,t\in I$ можна ввести відображення $\Gamma (\gamma )_{s}^{t},$ що кожному вектору $X\in T_{\gamma (s)}S$ ставить у відповідність вектор $\Gamma (\gamma )_{s}^{t}(X)\in T_{\gamma (t)}S$ одержаний паралельним перенесенням вектора X вздовж кривої. З властивостей лінійних диференціальних рівнянь випливає, що $\Gamma (\gamma )_{s}^{t},$ є невиродженим лінійним відображенням.
Якщо $X(t),Y(t)$ — паралельні векторні поля вздовж кривої $\gamma \colon I\to S$ , то $\langle X(t),Y(t)\rangle =const.$ Зокрема довжини векторів паралельного поля є сталими, як і кут між векторами двох довільних паралельних векторних полів. Це випливає з того, що згідно означення коваріантної похідної і паралельного поля $\langle X(t),{\dot {Y}}(t)\rangle =\langle {\dot {X}}(t),Y(t)\rangle =0.$ Тому ${\frac {d}{dt}}\langle X(t),Y(t)\rangle =\langle {\dot {X}}(t),Y(t)\rangle +\langle X(t),{\dot {Y}}(t)\rangle =0.$

Паралельне перенесення на векторному розшаруванні

Означення і властивості паралельних векторних полів для поверхонь у тривимірних полях легко переносяться на гіперповерхні у багатовимірних просторах. Більш загально його можна ввести для многовидів із їх дотичними розшаруваннями або навіть для векторних розшарувань над многовидами.

Нехай M — гладкий многовид. Нехай E → M — векторне розшарування із зв'язністю ∇ і γ:I → M — гладка крива, параметризована відкритим інтервалом I. Перетин $X$ з $E$ уздовж γ називається паралельним якщо

\nabla _{{\dot {\gamma }}(t)}X=0,\;t\in I.\,

Припустимо, що нам задано елемент e₀ ∈ E_P у P = γ(0) ∈ M, а не перетин. Паралельним перенесенням e₀ уздовж γ називається продовження e₀ до паралельного перетину X на γ. Точніше, X є єдиним перетином E вздовж кривої γ, для якого

$\nabla _{\dot {\gamma }}X=0$
$X_{\gamma (0)}=e_{0}.$

Зазначимо, що, як і у випадку регулярних поверхонь, в будь-якому заданому координатному околі (1) є є системою лінійних звичайних диференціальних рівнянь, з початковими умовами, заданими (2). Таким чином, теорема Пікара — Лінделефа гарантує існування та єдиність розв'язку.

Зв'язність ∇ визначає спосіб перенесення елементів шарів уздовж кривої і (оскільки відповідні диференціальні рівняння є лінійними) лінійні ізоморфізми між шарами розшарування у точках вздовж кривої:

\Gamma (\gamma )_{s}^{t}:E_{\gamma (s)}\rightarrow E_{\gamma (t)}

з векторного простору, над точкою γ(s) у векторний простір, над точкою γ(t). Цей ізоморфізм називається відображенням паралельного перенесення, пов'язаним з кривою. Ізоморфізми між шарами, отримані таким способом, загалом залежатимуть від вибору кривої: якщо такої залежності немає, то паралельне перенесення уздовж кожної можна використати для введення паралельних перетинів Е на всьому M. Це можливо лише у тому випадку, якщо кривина зв'язності ∇ є рівною нулю.

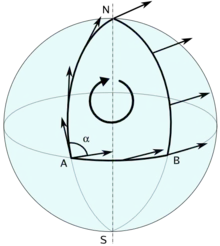
Зокрема, паралельне перенесення навколо замкнутої кривої, починаючи з точки x, визначає автоморфізм дотичного простору у точці x, що не обов'язково має тривіальне значення. Такі автоморфізми для всіх замкнутих кривих, для точки x, утворюють групу, що називається групою голономій зв'язності ∇ у точці x.

Існує тісний зв'язок між цією групою і значенням кривини ∇ у x; (теорема Емброуза — Сінгера).

Відновлення зв'язності з паралельного перенесення

Для коваріантної похідної ∇, паралельне перенесення вздовж кривої γ одержується шляхом інтегрування диференціального рівняння $\scriptstyle {\nabla _{\dot {\gamma }}=0}$ . Навпаки, якщо є деяке поняття паралельного перенесення, що задовольняє необхідні умови то відповідну зв'язність можна отримати диференціюванням.

Розглянемо для кожної кривої γ у многовиді набір лінійних відображень

\Gamma (\gamma )_{s}^{t}:E_{\gamma (s)}\rightarrow E_{\gamma (t)}

Нехай γ — диференційовна крива в M з початковою точкою γ(0) та початковим дотичним вектором X. Якщо V є гладким перетином E над γ, то

\nabla _{X}V=\lim _{h\to 0}{\frac {\Gamma (\gamma )_{h}^{0}V_{\gamma (h)}-V_{\gamma (0)}}{h}}=\left.{\frac {d}{dt}}\Gamma (\gamma )_{t}^{0}V_{\gamma (t)}\right|_{t=0}.

Справді, нехай $\xi _{1},\ldots ,\xi _{n}$ — деякий базис шару над $\gamma (0)$ і $\xi _{1}(t),\ldots ,\xi _{n}(t)$ — вектори одержані паралельним перенесенням (в кожному випадку одержується знову ж базис відповідного векторного простору оскільки оператори паралельного перенесення є невиродженими). Нехай у цих базисах $V(t)=V_{\gamma (t)}=\sum V_{i}(t)\xi _{i}(t).$ Згідно означення зв'язності:

\nabla _{{\dot {\gamma }}(t)}V(t)=\sum {\dot {V}}_{i}(t)\xi _{i}(t)+\sum V_{i}(t)\nabla _{{\dot {\gamma }}(t)}\xi _{i}(t)=\sum {\dot {V}}_{i}(t)\xi _{i}(t).

З іншого боку

{\frac {d}{dt}}\left(\Gamma {\gamma }_{t}^{0}(V(t))\right)|_{t=0}={\frac {d}{dt}}\left(\Gamma {\gamma }_{t}^{0}\left(\sum V_{i}(t)\xi _{i}(t)\right)\right)|_{t=0}={\frac {d}{dt}}\left(\sum V_{i}(t)\xi _{i}(0)\right)|_{t=0}=\sum {\dot {V}}_{i}(0)\xi _{i}(0),

що завершує доведення.

Якщо для кожної кривої γ у многовиді дано набір лінійних відображень

\Gamma (\gamma )_{s}^{t}:E_{\gamma (s)}\rightarrow E_{\gamma (t)},

що задовольняють умови

$\Gamma (\gamma )_{s}^{s}=Id$ , тотожне відображення E_(s).
$\Gamma (\gamma )_{u}^{t}\circ \Gamma (\gamma )_{s}^{u}=\Gamma (\gamma )_{s}^{t}.$
залежності Γ від γ, s, і t є гладкими у певному сенсі.

то ввівши диференціальний оператор:

\nabla _{X}V=\lim _{h\to 0}{\frac {\Gamma (\gamma )_{h}^{0}V_{\gamma (h)}-V_{\gamma (0)}}{h}}=\left.{\frac {d}{dt}}\Gamma (\gamma )_{t}^{0}V_{\gamma (t)}\right|_{t=0},

отримаємо зв'язність. Тобто фактично два поняття паралельного перенесення і зв'язності є тотожними і одне можна одержати з іншого.

Поняття гладкості в умовах 3 вимагає загалом деяких додаткових понять і часто є простішою для більш загальних понять паралельного перенесення.

Спеціальний випадок: дотичне розшарування

Нехай M — гладкий многовид. Тоді зв'язність на дотичному розшаруванні M, яка називається афінною зв'язністю є частковим випадком зв'язності на векторних розшаруваннях. Перетини векторного розшарування у цьому випадку є векторними полями. Відповідно векторне поле Y вздовж гладкої кривої γ:I → M називається паралельним якщо воно задовольняє умові $\nabla _{{\dot {\gamma }}(t)}X(t)=0.$

Нехай $x_{1},\ldots ,x_{n}$ — локальні координати в деякому координатному околі і $X_{1},\ldots ,X_{n}$ — відповідні їм векторні поля. За означенням символи Крістофеля вводяться із співвідношень $\nabla _{X_{k}}X_{j}=\sum _{i}\Gamma _{jk}^{i}X_{i}.$ Якщо образ кривої γ:I → M належить цьому координатному околу то можна ввести позначення

x_{i}(t)=x_{i}(\gamma (t)),\;X_{i}(t)=X_{i}(\gamma (t)),\;\Gamma _{ij}^{k}(t)=\Gamma _{ij}^{k}(\gamma (t)),\;Y(t)=Y(\gamma (t)).

При цих позначеннях можна записати $Y(t)=\sum a_{i}(t)X(t)$ і ${\dot {\gamma }}(t)=\sum {\dot {x}}_{i}(t)X(t).$ Тоді локально умову паралельності векторних полів можна записати як лінійну систему диференціальних рівнянь:

\sum _{i}\left[{\dot {a}}_{i}(t)X_{i}(t)+a_{i}(t)\sum _{j}{\dot {x}}_{j}(t)\Gamma _{ij}^{k}(t)X_{k}(t)\right]=0

або прирівнявши до нуля всі компоненти

{\dot {a}}_{k}(t)+\sum _{ij}a_{i}(t){\dot {x}}_{j}(t)\Gamma _{ij}^{k}(t)=0,\;\forall k\in 1,\ldots ,n.

При цьому виділяється клас кривих, що називаються (афінними) геодезичними. Гладка крива γ : I → M є афінною геодезичною, якщо ${\dot {\gamma }}$ є паралельним векторним полем уздовж $\gamma$ , тобто

\Gamma (\gamma )_{s}^{t}{\dot {\gamma }}(s)={\dot {\gamma }}(t).\,

Продиференціювавши це співвідношення можна записати:

\nabla _{{\dot {\gamma }}(t)}{\dot {\gamma }}=0.\,

Паралельне перенесення в рімановій геометрії

В (псевдо) рімановій геометрії, метрична зв'язність — зв'язність, відображення паралельного перенесення для якої зберігає метричний тензор. Таким чином, метрична зв'язність це будь-яка зв'язність Γ така, що для будь-яких двох векторів X, Y ∈ T_γ_(s)

\langle \Gamma (\gamma )_{s}^{t}X,\Gamma (\gamma )_{s}^{t}Y\rangle _{\gamma (t)}=\langle X,Y\rangle _{\gamma (s)}.

Взявши похідну при t = 0, пов'язаний диференційний оператор ∇ повинен відповідати правилу добутку щодо показника:

Z\langle X,Y\rangle =\langle \nabla _{Z}X,Y\rangle +\langle X,\nabla _{Z}Y\rangle .

Геодезичні

Якщо ∇ є метричною зв'язністю, то афінні геодезичні є звичайними геодезичними ріманової геометрії і є локально мінімальними кривими відстанями. Точніше, спочатку слід зазначити, що якщо γ : I → M, де I є відкритим інтервалом, є геодезичною, тоді норма ${\dot {\gamma }}$ є сталою на I. Дійсно,

{\frac {d}{dt}}\langle {\dot {\gamma }}(t),{\dot {\gamma }}(t)\rangle =2\langle \nabla _{{\dot {\gamma }}(t)}{\dot {\gamma }}(t),{\dot {\gamma }}(t)\rangle =0.

Узагальнення

Більш загальні поняття паралельного перенесення можна ввести для інших типів зв'язності.

Нехай P → M — головне розшарування над многовидом M зі структурною групою Лі G і зв'язністю ω. Як і у випадку векторних розшарувань, зв'язність ω на P визначає для кожної кривої γ в M, відображення

\Gamma (\gamma )_{s}^{t}:P_{\gamma (s)}\rightarrow P_{\gamma (t)}

з шару, над точкою γ(s) у шар, над точкою γ(t), що є ізоморфізмом однорідних просторів: тобто $\Gamma _{\gamma (s)}gu=g\Gamma _{\gamma (s)}$ для кожного g∈G.

Можливі також подальші узагальнення паралельного перенесення. У контексті зв'язності Ересмана, де зв'язність залежить від спеціального поняття горизонтального підйому.

Див. також

Література

Carmo, Manfredo Perdigão do (1976). Differential geometry of curves and surfaces. Upper Saddle River, NJ: Prentice-Hall. ISBN 0-13-212589-7.
do Carmo, Manfredo Perdigao (1994). Riemannian Geometry. Birkhauser. ISBN 978-0-8176-3490-2.
Darling, R. W. R. (1994). Differential Forms and Connections. Cambridge, UK: Cambridge University Press. ISBN 0-521-46800-0.
Guggenheimer, Heinrich (1977). Differential Geometry. Dover. ISBN 0-486-63433-7.
Kobayashi, Shoshichi; Nomizu, Katsumi (1996) [1963]. Foundations of Differential Geometry, Vol. 1. Wiley Classics Library. New York: Wiley Interscience. ISBN 0-471-15733-3.
Madsen, I. H.; Tornehave, J (1997). From Calculus to Cohomology: De Rham Cohomology and Characteristic Classes. Cambridge University Press. ISBN 978-0521580595.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.