Перелік розподілів імовірності
Багато розподілів імовірності, які важливі в теорії або застосуванні, отримали окремі назви.
Дискретні розподіли
Фінітні
- Розподіл Бернуллі, яке приймає значення 1 з ймовірністю p та значення 0 з ймовірністю q = 1 − p .
- Розподіл Радемахера, який приймає значення 1 з ймовірністю 1/2 і значення − 1 з ймовірністю 1/2.
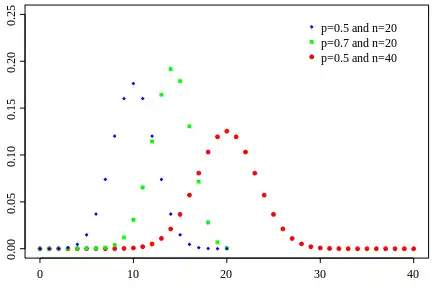
- Біноміальний розподіл, який описує кількість успіхів у серії незалежних експериментів «так/ні» з однаковою ймовірністю успіху.
- Бета-біноміальний розподіл, який описує кількість успіхів у серії незалежних експериментів Так/Ні з неоднорідністю ймовірності успіху.
- Вироджений розподіл при x 0, де X точно прийме значення x 0 . Це не виглядає випадковим, але задовольняє визначенню випадкової величини . Це корисно, оскільки ставить детерміновані змінні та випадкові змінні в один формалізм.
- Дискретний рівномірний розподіл, де всі елементи скінченної множини однаково ймовірні. Це теоретична модель розподілу збалансованої монети, неупередженого кубика, рулетки казино або першої карти добре перемішаної колоди.
- Гіпергеометричний розподіл, який описує число успіхів в перших т у серії п послідовних експериментів Так / Ні, якщо загальне число успіхів відомо. Такий розподіл виникає, коли немає заміни.
- Негативний гіпергеометричний розподіл, який описує кількість спроб, необхідних для досягнення n -го успіху в серії експериментів «так/ні» без заміни.
- Біноміальний розподіл Пуассона, який описує кількість успіхів у серії незалежних експериментів Так/Ні з різною ймовірністю успіху.
- Нецентральний гіпергеометричний розподіл Фішера
- Нецентральний гіпергеометричний розподіл Валленіуса
- Закон Бенфорда, який описує частоту першої цифри багатьох природних даних.
- Ідеальні та надійні розподіли солітонів .
- Закон Зіффа або розподіл Зіффа. Дискретний степеневий розподіл, найбільш відомим прикладом якого є опис частоти слів в англійській мові.
- Закон Зіпфа – Мандельброта - це дискретний степеневий розподіл, який є узагальненням розподілу Зіпфа .
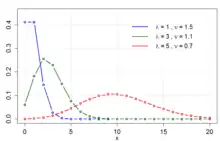
Розподіл Конвея – Максвелла – Пуассона
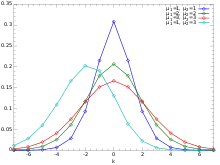
Розподіл Скеллама
З нескінченним носієм функції
- Бета -негативний біноміальний розподіл
- Розподіл Больцмана, дискретний розподіл, важливий у статистичній фізиці, який описує ймовірності різних рівнів дискретної енергії системи в тепловій рівновазі . Він має безперервний аналог. Особливі випадки включають:
- Розподіл Гіббса
- Розподіл Максвелла – Больцмана
- Розподіл Бореля
- Розширений негативний біноміальний розподіл
- Узагальнений розподіл логарифмічних рядів
- Розподіл Гаусса – Кузьміна
- Геометричний розподіл - дискретний розподіл, який описує кількість спроб, необхідних для досягнення першого успіху в серії незалежних випробувань Бернуллі, або, альтернативно, лише кількість втрат до першого успіху (тобто на одну спробу менше).
- Логарифмічний (послідовний) розподіл
- Негативний біноміальний розподіл або розподіл Паскаля, узагальнення геометричного розподілу до n -го успіху.
- Дискретний складний розподіл Пуассона
- Параболічний фрактальний розподіл
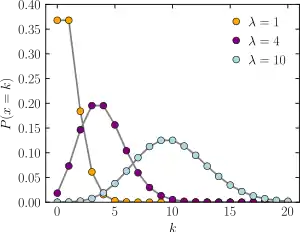
- Розподіл Пуассона, який описує дуже велику кількість індивідуальних малоймовірних подій, що відбуваються в певному часовому інтервалі. З цим розподілом пов'язана низка інших розподілів: зміщений Пуассон, гіперпуассон, загальний біноміал Пуассона та розподіли типу Пуассона.
- Розподіл Конвея – Максвелла – Пуассона, двопараметричне розширення розподілу Пуассона з регульованою швидкістю спаду.
- Обмежений нулем розподіл Пуассона для процесів, у яких нульовий рахунок не спостерігається
- Розподіл Полі – Еггенбергера
- Розподіл Скеллама, розподіл різниці між двома незалежними розподіленими Пуассоном випадковими величинами.
- Косий еліптичний розподіл
- Розподіл Юля – Саймона
- Розподіл дзета, що має застосування у прикладній статистиці та статистичній механіці, і, можливо, може бути корисним для теоретиків чисел. Це розподіл Zipf для нескінченної кількості елементів.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.