Інтеграл вздовж траєкторій

Інтеграл вздовж траєкторій — математичний оператор, який використовується у Фейнмановому формулюванні квантової механіки.

Ілюстрація дерева шляхів, які ведуть з точки A в точку B

Формальне визначення інтегралу вздовж траєкторій дається формулою

\int \limits _{W[t_{0},t]}(\ldots )D[q(t)]=\lim \limits _{n\rightarrow \infty ,\varepsilon \rightarrow 0}\left({\frac {m}{2\pi i\hbar \varepsilon }}\right)^{(n+1)/2}\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty }(\ldots )dq_{1}\ldots dq_{n}

,

де $\varepsilon (n+1)=t-t_{0}$ , $W[t_{0},t]\,$ — множина всіх траєкторій, які сполучають початкову точку $(q_{0},t_{0})\,$ та кінцеву точку $(q,t)\,$ , m — маса квантової частинки, $\hbar$ — зведена стала Планка.

Постулатом Фейманового формулювання квантової механіки є те, що пропагатор задається інтегралом вздовж траєкторій:

K(qt|q_{0}t_{0})=\int \limits _{W[t_{0},t]}\exp \left({\frac {i}{\hbar }}S[q(\cdot );t_{0},t]\right)D[q(t)]

,

де $S[q(\cdot );t_{0},t]$ — класична дія.

Якісна інтерпретація

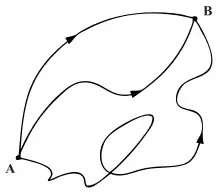
На відміну від звичайного інтеграла, в якому підсумовуються значення функції на відрізку, в інтегралі вздовж траєкторій підсумовуються значення функції вздовж усіх можливих кривих, які сполучають початкову й кінцеву точку. В рамках Фейнманового формулювання квантової механіки такий інтеграл визначає амплітуду ймовірності того, що квантова частинка переміститься з початкової точки в кінцеву.

Якщо в класичній механіці реалізується та з траєкторій, якій відповідає найменше значення дії, то в квантовій механіці свій вклад в ймовірність переходу частинки з однієї точки в іншу вносять усі можливі криві, які сполучають ці точки. Оскільки в квантовій механіці визначається не ймовірність переходу, а амплітуда ймовірності, то внески різних траєкторій інтерферують.

Інтеграл вздовж траєкторій у фазовому просторі

Квантову механіку можна сформулювати через інтеграли вздовж траєкторій, використовуючи також канонічні змінні — координату та імпульс. Пропагатор частинки задається при такому підході через співвідношення:

K(qt|q_{0}t_{0})=\int \limits _{W[t_{0},t]}\exp \left({\frac {i}{\hbar }}\int _{t_{0}}^{t}(p{\dot {q}}-{\mathcal {H}}(q,p))dt\right)D[q(t)]D[p(t)]

,

де ${\mathcal {H}}$ — функція Гамільтона.

Інтегрування проводиться вздовж усіх траєкторій у фазовому просторі із фіксованим значенням координати в початковій та кінцевій точках.

Статистична механіка

В квантовій статистичній механіці зележна від температури матриця густини задовольняє рівнянню

-{\frac {\partial {\hat {\rho }}}{\partial \beta }}={\hat {H}}{\hat {\rho }}

,

де $\beta ={\frac {1}{k_{B}T}}$ , $k_{B}$ — стала Больцмана.

Формальний розв'язок цього рівняння

{\hat {\rho }}(\beta )=e^{-\beta {\hat {H}}}{\hat {\rho }}(0)

.

Статистична сума дорівнює сліду від матриці густини

Z={\text{Sp}}\,{\hat {\rho }}

.

Вводячи умовний «час» $u=\beta \hbar$ , де $\hbar$ — зведена стала Планка, і розбиваючи інтервал [0, U] на дрібні інтервали, можна записати

{\hat {\rho }}(U)=\int \limits _{W(0,U)}\Phi [u]D[u]

,

розглядаючи всі можливі траєкторії, якими система може переміститися з початкового стану при нескінченно високій температурі в кінцевий стан при температурі, що визначається значенням U.

Історія

Формулювання квантової механіки через інтеграли вздовж траєкторій розробив у 1948 році Річард Фейнман.

Література

Вакарчук І.О. Квантова механіка. — 4-е видання, доповнене. — Л. : ЛНУ ім. Івана Франка, 2012. — 872 с.
Юхновський І.Р. Основи квантової механіки. — К. : Либідь, 2002. — 392 с.
Зи Э. Квантовая теория поля в двух словах. — Ижевск : РХД, 2009. — 632 с.
Зинн-Жюстен Ж. Континуальный интеграл в квантовой механике. — М. : Физматлит, 2010. — 360 с.
Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. — М. : Мир, 1968. — 384 с.
Simon B. Functional Integration and Quantum Physics. — Academic Press, 1979.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.