Інверсія кривої

Якщо пряма проходить через початок координат, її рівняння в полярних координатах буде θ = θ₀, де θ₀ сталий. Рівняння не змінюється за інверсії.

Рівняння в полярних координатах прямої, що не проходить через початок координат,

${\displaystyle r\cos(\theta -\theta _{0})=a}$

і рівнянням інверсії кривої буде

${\displaystyle r=a\cos(\theta -\theta _{0})}$

яке задає коло, що проходить через початок координат. Застосування інверсії вже до цього кола показує, що інверсією кола, яке проходить через початок координат, буде пряма.

У полярних координатах загальне рівняння кола, що не проходить через початок координат, має вигляд

${\displaystyle r^{2}-2r_{0}r\cos(\theta -\theta _{0})+r_{0}^{2}-a^{2}=0\quad (a,\ r>0,\ a\neq r_{0}),}$

де a — радіус і (r₀, θ₀) — полярні координати центра. Рівнянням інверсної кривої буде

${\displaystyle 1-2r_{0}r\cos(\theta -\theta _{0})+(r_{0}^{2}-a^{2})r^{2}=0,}$

або

${\displaystyle r^{2}-{\frac {2r_{0}}{r_{0}^{2}-a^{2}}}r\cos(\theta -\theta _{0})+{\frac {1}{r_{0}^{2}-a^{2}}}=0.}$

Це рівняння кола з радіусом

${\displaystyle A={\frac {a}{|r_{0}^{2}-a^{2}|}}}$

і центром у точці з координатами

${\displaystyle (R_{0},\ \Theta _{0})=\left({\frac {r_{0}}{r_{0}^{2}-a^{2}}},\ \theta _{0}\right).}$

Зауважимо, що R₀ може бути від'ємним.

Якщо початкове коло перетинається з одиничним колом, то центри цих двох кіл і точка перетину утворюють трикутник зі сторонами 1, a, r₀ і цей трикутник буде прямокутним, якщо

${\displaystyle r_{0}^{2}=a^{2}+1.}$

Але з рівняння вище випливає, що прочаткове коло збігається з його інверсією тільки в разі, коли

${\displaystyle r_{0}^{2}-a^{2}=1.}$

Таким чином, інверсія кола збігається з початковим колом тоді й лише тоді, коли коло перетинає одиничне коло під прямими кутами.

Рівнянням параболи, якщо повернути її так, щоб вісь стала горизонтальною, буде x = y². У полярних координатах це перетворюється на

${\displaystyle r={\frac {\cos \theta }{\sin ^{2}\theta }}.}$

Рівнянням інверсної кривої тоді буде

${\displaystyle r={\frac {\sin ^{2}\theta }{\cos \theta }}=\sin \theta \tan \theta }$,

і це цисоїда Діокла.

Рівняння в полярних координатах конічного перетину з фокусом у початку координат, з точністю до подібності

${\displaystyle r={\frac {1}{1+e\cos \theta }}}$,

де e — ексцентриситет. Інверсією цієї кривої буде:

${\displaystyle r=1+e\cos \theta }$,

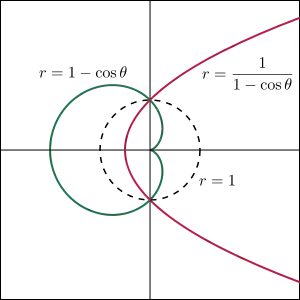
і це — рівняння равлика Паскаля. Якщо e = 0, це коло інверсії. Якщо 0 < e < 1, початкова крива є еліпсом і її інверсія — це замкнута крива з ізольованою точкою в початку координат. Якщо e = 1, початкова крива є параболою і її інверсія є кардіоїдою, що має касп у початку координат. Якщо e > 1, початкова крива є гіперболою і її інверсія утворює дві петлі з точкою перетину на початку координат.

Загальним рівнянням еліпса або гіперболи є:

${\displaystyle {\frac {x^{2}}{a^{2}}}\pm {\frac {y^{2}}{b^{2}}}=1}$.

Перетворимо рівняння так, щоб початок координат став вершиною:

${\displaystyle {\frac {(x-a)^{2}}{a^{2}}}\pm {\frac {y^{2}}{b^{2}}}=1}$,

і після перетворення:

${\displaystyle {\frac {x^{2}}{2a}}\pm {\frac {ay^{2}}{2b^{2}}}=x}$

або, замінивши константи:

${\displaystyle cx^{2}+dy^{2}=x}$.

Зауважимо, що парабола, розглянута вище, тепер потрапляє в цю схему, якщо покласти c = 0 і d = 1. Рівнянням інверсної кривої буде:

${\displaystyle {\frac {cx^{2}}{(x^{2}+y^{2})^{2}}}+{\frac {dy^{2}}{(x^{2}+y^{2})^{2}}}={\frac {x}{x^{2}+y^{2}}}}$

або

${\displaystyle x(x^{2}+y^{2})=cx^{2}+dy^{2}}$.

Це рівняння описує сімейство кривих, які називаються конхоїдами Слюза. Це сімейство включає, на додачу до цисоїди Діокла, описаної вище, трисектрису Маклорена (d = −c/3) і праву строфоїду (d = −c).

Рівняння еліпса або гіперболи:

${\displaystyle cx^{2}+dy^{2}=1}$,

після операції інвертування:

${\displaystyle (x^{2}+y^{2})^{2}=cx^{2}+dy^{2}}$

і це — лемніската Бута. Якщо d = −c, це лемніската Бернуллі.

Інверсія конічного перетину (відмінного від кола) є циркулярною кривою третього порядку, якщо центр інверсії лежить на кривій, і біциркулярною кривою четвертого порядку в іншому випадку. Конічні перетини є раціональними, так що інвертовані криві теж раціональні. І навпаки, будь-яка раціональна циркулярна крива третього порядку або раціональна біциркулярна крива четвертого порядку є інверсією конічного перетину. Фактично будь-яка з цих кривих повинна мати особливість, і якщо взяти цю точку за центр інверсії, інверсна крива буде конічним перетином[1][2].