Абстрактний багатогранник
У математиці абстрактний багатогранник, неформально кажучи, це структура, яка враховує тільки комбінаторні властивості традиційних багатогранників і ігнорує багато інших їхніх властивостей, таких як кути, довжини ребер тощо. При цьому не потрібна наявність будь-якого простору, що містить багатогранник, такого як евклідів простір. Абстрактне формулювання реалізує комбінаторні властивості як частково впорядковану множину (далі посет[1]).

Абстрактне визначення дозволяє деякі більш загальні комбінаторні структури, ніж традиційна концепція багатогранника, і допускає багато нових об'єктів, що не мають аналога в традиційній теорії.
Традиційні багатогранники в порівнянні з абстрактними
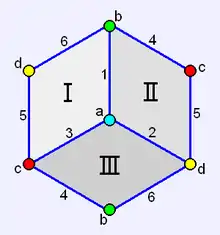
В геометрії Евкліда шість чотирикутників, наведених на малюнку вище, різні. Все ж вони мають щось спільне, що відрізняє їх від трикутника або куба, наприклад.
Елегантна, хоча географічно неточна, схема лондонського метро надає всю відповідну інформацію як проїхати з пункту A в пункт B. Ще один приклад — електрична принципова схема. За нею кінцеве розташування проводів і елементів часто з першого погляду визначити неможливо.
У кожному такому прикладі зв'язки між елементами ті ж самі і не пов'язані з фізичним розташуванням. У цьому випадку кажуть, що об'єкти комбінаторно еквівалентні. Ця еквівалентність і укладена в поняття абстрактного багатогранника. Таким чином, комбінаторно наші шість чотирикутників «ті ж самі». Кажучи строгіше, вони ізоморфні або «зберігають структуру».
Властивості, зокрема вимірні, традиційних багатогранників, такі як кути, довжина ребер, несиметрія і опуклість несуттєві для абстрактних багатогранників. Інші традиційні поняття можуть розглядатися, але не завжди таким самим чином. Може трапитися, що деяке судження, істинне для традиційних багатогранників, може бути хибним для абстрактних, і навпаки. Наприклад, традиційні багатогранники правильні, якщо всі їхні грані і вершинні фігури правильні, але це не стосується абстрактних багатогранників [2].
Вступні поняття
Для визначення абстрактних багатогранників слід увести кілька понять.
У цій статті багатогранник означає абстрактний багатогранник, якщо не зазначено явно інше. Термін традиційний використовується для посилань на те, що зазвичай розуміється під багатогранниками за винятком власне абстрактних багатогранників. Іноді використовуються терміни класичний або геометричний.
Багатогранники як частково впорядковані множини
Зв'язки на схемі залізниці або електричній схемі можна подати просто «точками і лініями», тобтографом. Багатогранники, однак, мають ієрархію за розмірністю. Наприклад, вершини, ребра і грані куба мають розмірності 0, 1 і 2 відповідно. Сам куб є 3-вимірним.
У цій абстрактній теорії поняття рангу замінює поняття розмірності. Це поняття формально визначено нижче.
Поняття грань використовується для будь-яких елементів будь-якого рангу, наприклад вершин (ранг 0) або ребер (ранг 1), а не тільки граней рангу 2. Елемент рангу k називається k-гранню.
Можемо тоді визначити багатогранник як множину граней P з відношенням порядку <, яке задовольняє додатковим аксіомам. Формально, P (з відношенням порядку <) буде (строго) частково впорядкованою множиною (посет[1]).
Якщо F < G, ми кажемо, що F є підгранню G (або G має підгрань F).
Ми кажемо, що F і G інцидентні, якщо або F = G, або F < G, або G < F. Це значення відрізняється від традиційного використання в геометрії та інших галузях математики. Наприклад, у квадраті abcd, ребра ab і bc НЕ інцидентні.
Найменші і найбільші грані
Так само як поняття нуля і нескінченності є необхідними в математиці, такі ж поняття корисні для абстрактних багатогранників — вважається що будь-який багатогранник має найменшу грань, яка є підгранню всіх інших, і найбільшу грань, для якої всі інші грані є підгранями.
Фактично, багатогранник може мати лише одну грань. В цьому випадку найменша і найбільша грані збігаються.
Найменшу і найбільшу грані називають невласними. Всі інші грані називають власними.
Найменшу грань називають порожньою гранню, оскільки вона не має вершин (або будь-яких інших граней) як підграней. Оскільки найменша грань міститься нижче за рівнем від вершин (граней нульового рангу), її ранг дорівнює -1. Ми позначаємо цю грань як F−1. Якщо це здається на перший погляд дивним, це почуття швидко зникає, коли розумієш, яку симетрію це поняття вносить у теорію. (Історично, математики противились таким поняттям, як від'ємні числа, дробові, ірраціональні і комплексні числа, і навіть нуль!)
Простий приклад
Як приклад тепер створимо абстрактний квадрат з гранями як у таблиці:
| Тип грані | Ранг (k) | Число | k-грані |
|---|---|---|---|
| Найменша | -1 | 1 | F −1 |
| Вершини | 0 | 4 | a, b, c, d |
| Ребра | 1 | 4 | W, X, Y, Z |
| Найбільша | 2 | 1 | G |
Відношення < визначається як множина пар, яка (для цього прикладу) включає
- F−1<a, ... , F−1<X, ... , F−1<G, ... , b<Y, ... , c<G, ... , Z<G.
У цьому прикладі ми могли б записати ребра W, X, Y і Z як ab, ad, bc і cd відповідно, і ми будемо часто використовувати такий варіант запису. Але, як ми незабаром побачимо, така система запису не завжди прийнятна.
Ми називаємо отриману фігуру квадратом, а не чотирикутником (або чотирибічником), оскільки в нашому абстрактному світі немає кутів і ребра не мають довжин. Всі чотири ребра ідентичні і «геометрія» в кожній вершині однакова.
Відношення порядку транзитивні, тобто з F < G і G < H випливає, що F < H. Таким чином, для опису ієрархії граней немає необхідності задавати всі випадки F < H, досить вказати для кожного елемента наступний елемент, тобто коли F < H і немає такого G, для якого F < G < H.
Діаграма Гассе
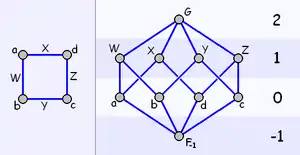
Малі посети, і багатогранники зокрема, часто добре візуалізуються за допомогою діаграми Гассе, як показано на рисунку. Зазвичай грані однакового рангу розміщуються на одному горизонтальному рівні. Кожна лінія між гранями відповідає парі F, G, такій що F < G, де F міститься на діаграмі нижче, ніж G.
Багатогранник часто малюють неформально як граф. Граф має вершини і ребра, але не має граней. Мало того, для більшості багатогранників неможливо отримати всі інші грані з графу, і, в загальному випадку, різні багатогранники можуть мати один граф.
Діаграма Гассе, з іншого боку, повністю описує будь посет — всі структури багатогранників покриваються діаграмами Гассе. Ізоморфні багатогранники дають ізоморфні діаграми Гассе і навпаки.
Ранг
Ранг грані F визначають як ціле (m − 2), де m — максимальна кількість граней в будь-якому ланцюжку (F', F", ... , F), що задовольняє F' < F" < ... < F.
Ранг посета P — це максимальний ранг n будь-якої грані, тобто ранг максимальної грані (як зазначено вище, будь-який багатогранник має максимальну грань). У цій статті ми завжди використовуємо n для позначення рангу посета або багатогранника.
Звідси випливає, що найменша грань, і ніяка інша, має ранг -1, а найбільша грань має ранг n. Ми позначаємо їх як F−1 і Fn відповідно.
Ранг грані або багатогранника зазвичай відповідає розмірності аналога в традиційній теорії, але не завжди. Наприклад, грань рангу 1 відповідає ребру, яке має розмірність 1. Але просторовий багатокутник у традиційній геометрії 3-вимірний, оскільки він не плоский. В абстрактному еквіваленті такий багатокутник залишається абстрактним багатокутником рангу 2.
Для деяких рангів існують назви типів граней.
| Ранг | -1 | 0 | 1 | 2 | 3 | … | n — 2 | n — 1 | n |
|---|---|---|---|---|---|---|---|---|---|
| Тип межі | Найменша | Вершина | Ребро | † | Комірка | Гіперребро | Гіпергрань | Найбільша |
† Хоча традиційно під «гранню» розуміють грань рангу 2, ми завжди будемо писати «2-грань», щоб уникнути двозначності і залишаємо термін «грань» для позначення грані будь-якого рангу.
Відрізок
_and_its_Hasse_Diagram.PNG.webp)
Відрізок — це посет, що має мінімальну грань, рівно дві 0-грані і найбільшу грань, наприклад {∅, a, b, ab}. Звідси випливає, що вершини a і b мають ранг 0, а найбільша грань ab, а тому й сам посет, мають ранг 1.
Прапори
Прапор — це максимальний ланцюжок граней, тобто (повністю) впорядкована множина Ψ граней, у якій кожна грань є підгранню наступної (якщо така є), і така, що Ψ не є підмножиною будь-якого більшого ланцюжка.
Наприклад, { ∅ , a, ab, abc} є прапором у трикутнику abc.
Ми будемо додатково вимагати, щоб для даного багатогранника всі прапори містили однакове число граней. Посети, в загальному випадку, не задовольняють цим вимогам. Посет {∅ , a, b, bc, abc} має 2 прапори нерівного розміру, а тому не є багатогранником.
Ясно, що якщо є дві різні грані F, G у прапорі, то або F < G або F > G.
Секції
Будь-яка підмножина P' посета P є посетом (з тим самим відношенням <, обмеженим на P').
Зокрема, якщо дано дві грані F, H посета P, де F ≤ H, множина {G | F ≤ G ≤ H} називають секцією посета P і позначають H/F. (У термінології теорії порядку секція має назву замкнутого інтервала посета і позначається [F, H], але поняття ідентичні).
Таким чином, P є секцією себе.
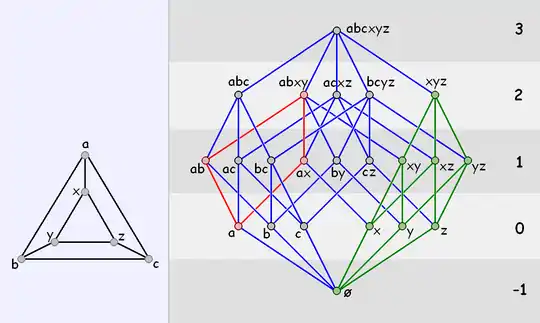
Наприклад, у призмі abcxyz (див. малюнок) секція xyz/ø (виділено зеленим кольором) є трикутником
- { ∅ , x, y, z, xy, xz, yz, xyz}.
k-секція — це секція рангу k.
Багатогранник, який є підмножиною іншого багатогранника, не обов'язково є секцією. Квадрат abcd є підмножиною тетраедра abcd, але не є його секцією.
Поняття секції не має того самого значення в традиційній геометрії.
Вершинні фігури
Вершинна фігура в заданій вершині V — це (n−1)-секція Fn/V, де Fn є найбільшою гранню.
Наприклад, у трикутнику abc вершинною фігурою в b, abc/b, є {b, ab, bc, abc}, тобто відрізок. Вершинними фігурами куба є трикутники.
Зв'язність
Посет P є зв'язним, якщо ранг P ≤ 1, або для будь-яких двох власних граней F і G існує послідовність власних граней: H1, H2, … , Hk
така, що F = H1, G = Hk і кожна грань Hi, i < k інцидентна попередній грані.
Умова вище забезпечує, що пара окремих трикутників abc і xyz не є (єдиним) багатогранником.
Посет P є строго зв'язним, якщо будь-яка секція P (включно з самим P) зв'язна.
З цією додатковою вимогою виключаються дві піраміди, що мають спільну вершину. Однак дві квадратні піраміди, наприклад, можуть бути «склеєні» квадратними гранями, що дає октаедр. У цьому випадку «спільна грань» не є гранню октаедра.
Формальне визначення
Абстрактний багатогранник — це частково впорядкована множина, елементи якої ми називаємо гранями, що задовольняє таким чотирьом аксіомам:
- Він має найменшу грань і найбільшу грань.
- Всі прапори містять одне і те саме число граней.
- Він строго пов'язаний.
- Будь-яка 1-секція є відрізком.
n-багатогранник є багатогранником рангу n.
Примітки
У разі порожнього багатогранника найменша і найбільша грані є одним і тим самим єдиним елементом.
Аксіома 2 еквівалентна твердженню, що посет є градуйованим посетом.
Якщо виконуються інші аксіоми, аксіома 3 еквівалентна строгій зв'язності прапорів, що неформально означає:
- Для будь-якої секції багатогранника (включно з самим багатогранником) будь-який прапор можна змінити в будь-який інший змінюючи лише одну грань за крок.
Аксіома 4 відома як «властивість діаманту», оскільки на діаграмі Гассе відрізок подається чотирикутником (діамантом).
З аксіом можна показати, що будь-яка секція є багатогранником і що Rank(G/F) = Rank(G) − Rank(F) − 1.
Найпростіші багатогранники
Ранг < 2
Є лише по одному багатограннику з рангами -1, 0 і 1, і це, відповідно, порожній багатогранник, точка і відрізок.
Для n ≤ 1 всі n-секції багатогранника є (унікальними) n-багатогранниками. Однак грані рангу 0 і 1 багатогранника називають вершинами і ребрами відповідно.
Ранг 2
Для будь-якого p, 3 ≤ p < є абстрактний еквівалент традиційного багатокутника з p вершинами і p ребрами, p-кутник. Для p = 3, 4, 5, … ми отримуємо трикутник, квадрат, п'ятикутник, ….
Дигон
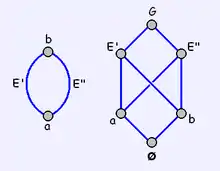
Дигон — це багатогранник з двома ребрами, що й відповідає назві. На відміну від інших багатокутників, обидва ребра мають дві спільні вершини. З цієї причини він вважається виродженим.
Досі ми використовували для визначення граней «вершинну нотацію», наприклад. {∅, a, b, c, ab, ac, bc, abc} для трикутника abc. Цей метод має певну перевагу перед заданням відношення <.
У випадку з дигоном і багатьма іншими абстрактними багатогранниками вершинну нотацію використовувати не можна. Ми мусимо дати граням індивідуальні назви і вказати пари підграней F < G (задати порядок).
Так, дигон слід визначити як множину {∅, a, b, E', E", G} з відношенням порядку <
- {ø<a, ø<b, a<E', a<E, b<E', b<E, E'<G, E"<G}
де E' і E" — два ребра, а G — найбільша грань.
Підсумовуючи, багатогранник можна повністю описати лише вершинною нотацією, якщо кожна грань має унікальний набір вершин. Багатогранник, який має таку властивість, називають атомарним.
Приклади вищого порядку
Як зазначалося вище, поняття абстрактного багатогранника дуже загальне і включає:
- Нескінченногранники, тобто нескінченні багатогранники або замощення
- Розкладання інших многовидів, таких як тор або дійсна проєктивна площина
- Багато інших об'єктів, таких як одинадцятикомірник і п'ятдесятисемикомірник, які не поміщаються звичним чином у «нормальні» геометричні простори.
В загальному випадку, множина j-граней (-1 ≤ j ≤ n) традиційного n-багатогранника утворює абстрактний n-багатогранник.
Осоедри
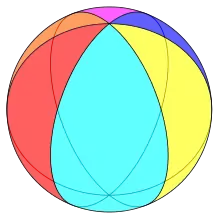
Дигон узагальнюється осоедрами, які можна реалізувати як сферичні багатогранники - замощення сфери.
Проєктивні багатогранники
Чотирма прикладами нетрадиційних абстрактних багатогранників є напівкуб[3] (показаний на малюнку), напівоктаедр, напівдодекаедр і напівікосаедр. Ці багатогранники є проєктивними двійниками правильних багатогранників і можуть бути реалізовані як проєктивні багатогранники — вони замощують дійсну проєктивну площину.
Напівкуб є ще одним прикладом, коли вершинна нотація незастосовна — всі 2-грані і 3-грані мають один і той самий набір вершин.
Двоїстість
Будь-який багатогранник має двоїстий, тобто багатогранник, у якому частковий порядок обернений — діаграма Гассе двоїстого багатогранника є такою ж, як і в оригінального, але перевернута («догори ногами»). Кожна початкова k-грань n-багатогранника переходить у (n − k − 1)-грань двоїстого. Так, наприклад, n-грань переходить в (-1)-грань. Двоїстий багатогранник двоїстому тотожний (ізоморфний) початковому.
Багатогранник є самодвоїстим, якщо він збігається зі своїм двоїстим багатогранником, тобто ізоморфний двоїстому. Таким чином, діаграма Гассе самодвоїстого багатогранника має бути симетричною відносно горизонтальної осі. Квадратна піраміда в прикладі вище є самодвоїстим багатогранником.
Вершинна фігура у вершині V є двоїстою відповідній грані двоїстого багатогранника.
Абстрактні правильні багатогранники
Формально, абстрактний багатогранник визначається як «правильний», якщо його група автоморфізмів діє транзитивно на множину його прапорів. Зокрема, будь-які дві k-грані F і G n-багатогранника є «однаковими», тобто є автоморфізм, який переводить F у G. Коли абстрактний багатогранник є правильним, його група автоморфізмів ізоморфна факторгрупі групи Коксетера.
Всі багатогранники рангу ≤ 2 правильні. Найвідоміші правильні багатогранники — п'ять платонових тіл. Напівкуб (показано на малюнку) є правильним.
Неформально це означає, що для кожного рангу k немає способу відрізнити яку-небудь k-грань від будь-якої іншої — грані мають бути однаковими і мати однакових сусідів, і так далі. Наприклад, куб є правильним, оскільки всі його грані є квадратами, кожна вершина квадрата належить трьом квадратам і кожен квадрат оточений однаково іншими гранями, ребрами і вершинами, і так далі.
Це умова без жодних доповнень є достатня для того, щоб абстрактний багатогранник мав ізоморфні правильні (n−1)-грані та ізоморфні правильні вершинні фігури.
Ця умова слабша, ніж правильність для традиційних багатогранників, оскільки вона стосується (комбінаторної) групи автоморфізмів, а не (геометричної) групи симетрії. Наприклад, будь-який абстрактний багатокутник є правильним, оскільки кути, довжини ребер, кривина ребер, перекіс тощо не існують для абстрактних багатогранників.
Існують деякі інші ослаблювальні поняття, деякі не цілком стандартизовані, такі як напівправильний, квазіправильний, однорідний, хіральний многогранники і архімедові тіла, застосовні до багатогранників, у яких деякі, але не всі грані еквівалентні для кожного рангу.
Приклад неправильного багатогранника
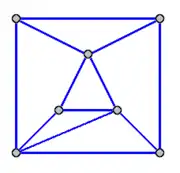
Якщо взяти до уваги, скільки місця приділено правильним багатогранникам, може здатися, що всі багатогранники правильні Насправді, правильні багатогранники є дуже частковими випадками.
Найпростішим неправильним багатогранником є квадратна піраміда, хоча вона має багато симетрій.
На малюнку наведено приклад багатогранника без нетривіальної симетрії — жодна пара вершин, ребер, або 2-граней не є «тими самими», як визначено вище. Можливо, це найпростіший з таких багатогранників.
Реалізації
Будь-який традиційний багатогранник є прикладом реалізації абстрактного багатогранника, що лежить у його основі. Це ж стосується замощень площини або інших кусково лінійних многовидів у розмірностях два і вище. До останніх належать, наприклад, проєктивні багатогранники. Їх можна отримати з багатогранників за допомогою центральної симетрії ототожненням протилежних вершин, ребер, граней і т. д. У тривимірному просторі це дає напівкуб і напівдодекаедр і їх двоїсті, напівоктаедр і напівікосаедр.
Більш загально, реалізація правильного абстрактного багатогранника — це набір точок у просторі (відповідних вершин багатогранника), разом зі структурою граней, породженою на них (абстрактним) багатогранником, і ця структура, щонайменше, має ті ж симетрії, що і вихідний абстрактний багатогранник. Тобто, всі комбінаторні автоморфізми абстрактних багатогранників реалізуються геометричними симетріями. Наприклад, набір точок {(0,0), (0,1), (1,0), (1,1)} є реалізацією абстрактного 4-кутника (квадрата). Однак це не єдина реалізація — можна вибрати замість цього вершини правильного тетраедра. Для будь-якої симетрії квадрата існує відповідна симетрія правильного тетраедра (однак, правильний тетраедр має більше симетрій, ніж абстрактний 4-кутник).
Фактично, будь-який абстрактний багатогранник з v вершинами має принаймні одну реалізацію як вершини (v − 1)-вимірного симплекса. Часто цікаво знайти реалізацію в найменшій розмірності.
Якщо абстрактний n-багатогранник можна реалізувати в n-вимірному просторі так, що геометричне розташування не порушує яких-небудь правил для традиційних багатогранників (таких як криволінійні грані або гребені[4] нульового розміру), про таку реалізацію кажуть як про правильну. В загальному випадку тільки обмежену множину абстрактних багатогранників рангу n можна реалізувати правильно для будь-якого n-простору.
Задача об'єднання і універсальні багатогранники
Базова теорія комбінаторних структур, які тепер відомі як «абстрактні багатогранники» (спочатку звані «incidence polytopes» — інциденціальні багатогранники), описана в докторській дисертації Егона Шульте, хоча вона ґрунтується на раніших роботах Бранко Ґрюнбаума, Гарольда Коксетера і Жака Тітса. Відтоді дослідження в теорії абстрактних багатогранників фокусувалися, переважно, на правильних багатогранниках, тобто багатогранниках, групи автоморфізмів яких діють транзитивно на множині прапорів багатогранника.
Важливим питанням у теорії абстрактних багатогранників є задача змішування. Задача складається із серії питань, таких як:
- Для заданих абстрактних багатогранників K і L, чи існує який-небудь багатогранник P, гіпергранями якого є багатогранник K, а вершинними фігурами — багатогранник L?
- Якщо так, чи є вони всі скінченними?
- Які скінченні багатогранники такого типу існують?
Наприклад, якщо K квадрат, а L — трикутник, відповіді на ці питання такі: Так, існують багатогранники P з квадратними гранями, з'єднаними по три в одній вершині (тобто, багатогранники типу {4,3}).
- Так, всі вони скінченні,
- Існує куб із шістьма квадратними гранями, дванадцятьма ребрами і вісьмома вершинами, і напівкуб із трьома гранями, шістьма ребрами і чотирма вершинами.
Відомо, що якщо відповідь на перше питання позитивна (Так) для деяких правильних K і L, існує єдиний багатогранник, гіпергранями якого є K, а вершинними фігурами якого є L. Цей багатогранник називається універсальним багатогранником з цими гіпергранями і вершинними фігурами, який покриває всі багатогранники цього типу. Тобто, припустимо, що P є універсальним багатогранником з гіпергранями K і вершинними фігурами L. Тоді будь-який інший багатогранник Q з цими гранями і вершинними фігурами можна записати Q=P/N, де
- N — підгрупа групи автоморфізмів P
- P/N є набором орбіт елементів P при діях N з частковим порядком, породженим групою P.
Q=P/N називається часткою від P, і кажуть, що P покриває Q.
Якщо враховувати цей факт, пошук багатогранників з вибраними гіпергранями і вершинними фігурами зазвичай відбувається за наступним сценарієм:
- Намагаємося знайти універсальний багатогранник
- Намагаємося класифікувати частки.
Ці дві задачі, в загальному випадку, дуже складні.
Повертаючись до прикладу вище, якщо K є квадратом, а L — трикутником, універсальним многогранником {K,L} буде куб (який записується як {4,3}). Напівкуб є відношенням {4,3}/N, де N — група симетрій (автоморфізмів) з двома елементами — тотожною симетрією і симетрією, що відображає кожен кут (ребро або грань) у протилежний елемент.
Якщо L є також квадратом, універсальним багатогранником {K,L} (тобто, {4,4}) є замощення евклідового простору квадратами. Це замощення має нескінченне число часток із квадратними гранями, по чотири на вершину, деякі з яких правильні, а деякі — ні. За винятком самого універсального багатогранника, всі частки відповідають різним способам замощення квадратами поверхні тора або нескінченно довгого циліндра.
Одинадцятикомірник і п'ятдесятисемикомірник
Одинадцятикомірник, незалежно відкритий Коксетером і Ґрюнбаумом, є абстрактним 4-вимірним багатогранником. Його гранями є напівікосаедри. Оскільки гіперграні є, топологічно, проєктивними площинами, а не сферами, одинадцятикомірник не є замощенням якогось многовиду в звичному сенсі. Замість цього одинадцятикомірник є локально проєктивним багатогранником. Одинадцятикомірник не тільки чудовий математично, він важливий як історично перший відкритий нетрадиційний абстрактний багатогранник. Багатогранник самодвоїстий і універсальний — це єдиний багатогранник з напівікосаедральними гіпергранями і напівдодекаедральними вертексними фігурами.
П'ятдесятисемикомірник також самодвоїстий, він має напівдодекаедральні гіперграні. Багатогранник знайшов Гарольд Коксетер невдовзі після відкриття одинадцятикомірника. Подібно до одинадцятикомірника він універсальний, єдиний багатогранник із напівдодекаедральними гіпергранями і напівікосаедральними вершинними фігурами. З іншого боку, існує багато інших багатогранників з напівдодекаедральними гіпергранями і символом Шлефлі {5,3,5}. Універсальний багатогранник з напівдодекаедральними гіпергранями й ікосаедральними (НЕ напівікосаедральними) вершинними фігурами скінченний, але дуже великий, він має 10 006 920 гіперграней і вдвічі менше вершин.
Локальна топологія
Завдання злиття, історично, стосувалася локальної топології. Тобто, замість обмеження K і L конкретними багатогранниками, дозволяються будь-які багатогранники із заданою топологією, тобто будь-яке замощення багатогранниками заданого многовида. Якщо K і L є сферичними (тобто, замощеннями топологічної сфери), то P називається локально сферичним і відповідає замощенню деякого многовида. Наприклад, якщо K і L є обидва квадратами (а тому, топологічно, колами), P буде замощенням площини, тора або пляшки Клейна квадратами. Замощення n-вимірного многовида, фактично, є багатогранником рангу n + 1. І це узгоджується з інтуїтивним уявленням, що платонові тіла тривимірні, навіть якщо їх можна розглядати як замощення поверхні двовимірної поверхні кулі.
У загальному випадку, абстрактний багатогранник називається локально X, якщо його гіперграні і вершинні фігури, топологічно, або сфери, або X, але не сфери одночасно. Одинадцятикомірник і п'ятдесятисемикомірник є прикладами локально проєктивних багатогранників рангу 4 (тобто, чотиривимірних), оскільки їхні гіперграні і вершинні фігури є замощеннями дійсних проєктивних площин. Тут, однак, існує слабкість термінології. Визначення не дає простих шляхів опису багатогранників, гіпергранями якого є тори, а вершинними фігурами — проєктивні площини, наприклад. Ще гірше, коли різні гіперграні мають різну топологію чи не мають визначеної топології взагалі. Однак значний крок зроблено щодо повної класифікації n локально тороїдальних правильних багатогранників[5].
Відображення обміну
Нехай Ψ — прапор абстрактного n-багатогранника і нехай -1 < i < n. З визначення абстрактного багатогранника можна довести, що є єдиний прапор, відмінний від Ψ тільки одним елементом рангу i і однаковий в іншому. Якщо ми позначимо такий прапор через Ψ(i), то це задає набір відображень прапорів багатогранника, скажімо φi. Ці відображення називаються відображеннями обміну, оскільки вони міняють місцями пари прапорів: (Ψφi)φi = Ψ[6]. Деякі інші властивості відображень обміну:
- φi2 тотожне відображення
- φi утворюють групу.
- якщо |i — j| > 1, 'φ'iφj = 'φ'jφi
- Якщо α — автоморфізм багатогранника, то αφi = φiα
- Якщо багатогранник правильний, то група, що генерується φi, ізоморфна групі автоморфізмів, в іншому випадку вона строго більша.
Відображення обміну можуть бути використані для доведення, що будь-який абстрактний багатогранник є похідним від деякого правильного багатогранника.
Матриці інциденцій
Багатогранник можна подати у вигляді таблиці інциденцій. Нижче наведено матрицю інциденцій для трикутника:
| ø | a | b | c | ab | bc | ca | abc | |
|---|---|---|---|---|---|---|---|---|
| ø | • | • | • | • | • | • | • | • |
| a | • | • | • | • | • | |||
| b | • | • | • | • | • | |||
| c | • | • | • | • | • | |||
| ab | • | • | • | • | • | |||
| bc | • | • | • | • | • | |||
| ca | • | • | • | • | • | |||
| abc | • | • | • | • | • | • | • | • |
Точка в таблиці показує, що одна грань є підгранню іншої грані (або навпаки, так що таблиця симетрична відносно діагоналі). Таким чином, таблиця містить надлишкову інформацію, досить було б показувати точку, коли номер грані рядка ≤ номера грані стовпця (верхню трикутну матрицю).
Оскільки саме тіло і порожня множина інцидентні всім іншим елементам, перший рядок і перший стовпець, а також останній рядок і останній стовпець тривіальні і їх можна опустити.
Подальшу інформацію можна отримати підрахунком інціденцій. Таке чисельне подання дозволяє групування за симетрією як у діаграмі Гассе квадратної піраміди — якщо вершини B, C, D і E еквівалентні за симетрією в абстрактному багатограннику, то ребра f, g, h і j групуються разом, і те саме для ребер k, l, m і n. Врешті-решт групуються і трикутники 'P', 'Q', 'R' і 'S'. Відповідна матриця інціденцій абстрактного багатогранника може виглядати так:
| A | B, C, D, E | f, g, h, j | k, l, m, n | P, Q, R, S | T | |
|---|---|---|---|---|---|---|
| A | 1 | * | 4 | 0 | 4 | 0 |
| B, C, D, E | * | 4 | 1 | 2 | 2 | 1 |
| f, g, h, j | 1 | 1 | 4 | * | 2 | 0 |
| k, l, m, n | 0 | 2 | * | 4 | 1 | 1 |
| P, Q, R, S | 1 | 2 | 2 | 1 | 4 | * |
| T | 0 | 4 | 0 | 4 | * | 1 |
У цій матриці інціденцій діагональні елементи дають загальне число елементів кожного типу.
Ясно, що елементи різних типів одного рангу ніколи не можуть бути інцидентними, так що значення завжди дорівнює 0, але щоб допомогти розпізнати це відношення в таблиці використовується зірочка (*) замість нуля.
Піддіагональні елементи таблиці для кожного рядка представляють число інціденцій відповідних піделементів, тоді як наддіагональні елементи представляють число інціденцій елемента вершинам, ребрам та іншим фігурам.
Вже цей приклад квадратної піраміди показує, що така матриця інциденцій не симетрична. Однак залишаються прості зв'язки елементів таблиці, оскільки для таких матриць інциденцій виконується:
Історія
Ранні приклади абстрактних багатогранників виявили Коксетер і Петрі — три нескінченні структури {4, 6}, {6, 4} і {6, 6}, які вони назвали правильними косими нескінченногранниками.
1960 року Бранко Ґрюнбаум запропонував геометричній спільноті обговорити узагальнення поняття правильних багатогранників, які він назвав polystromata (poly + stromata[7]). Він розробив теорію, показавши приклади нових об'єктів, включно з одинадцятикомірником.
Одинадцятикомірник є самодвоїстим чотиривимірним багатогранником, грані якого не ікосаедри, а напівікосаедри, тобто, фігури, які виходять, якщо протилежні сторони ікосаедра вважати однією (тією ж) гранню (Grünbaum, 1977). Через кілька років після відкриття Ґрюнбаумом одинадцятикомірника Коксетер виявив схожий багатогранник, пятдесятисемикомірник (Coxeter 1982, 1984), а потім, незалежно, перевідкрив одинадцятикомірник.
Егон Шульте (Egon Schulte) визначив «правильні комплекси інциденцій» і «правильні інциденційні багатогранники» в свій дисертації в 1980-х, у якій було вперше наведено сучасне визначення. Згодом він і Пітер Макмаллен розробили базову теорію в серії статей, пізніше зібраних у книгу. Численні дослідники зробили відтоді свій внесок, а піонери досліджень (зокрема Ґрюнбаум) прийняли визначення Шульте як «правильне».
Див. також
- Одинадцятикомірник і п'ятдесятисемикомірник — два абстрактних правильних 4-вимірних багатогранники
- Ейлерова частково впорядкована множина
- Градуйована частково впорядкована множина
- Правильний багатогранник
Примітки
- poset = partially ordered set = частково впорядкована множина
- McMullen, Schulte, 2002, с. 31.
- В англійській мові є два терміни, які можна перекласти як напівкуб — hemicube і demicube. У статті йдеться про hemicube.
- Гребінь — це грань розмірності n-2. Для тривимірних багатогранників гребінь збігається з ребром.
- McMullen, Schulte, 2002.
- Hartley, Hulpke, 2010, с. 107.
- polystromata = poly + stromata, stromata = множ. від stroma = основа, кістяк
Література
- Peter McMullen, Egon Schulte. Abstract Regular Polytopes. — 1st. — Cambridge University Press, 2002. — ISBN 0-521-81496-0.
- Jaron's World: Shapes in Other Dimensions, Discover mag., Apr 2007
- Dr. Richard Klitzing, Incidence Matrices
- E. Schulte. Handbook of discrete and computational geometry / J. E. Goodman, O'Rourke, J. — 2nd. — Chapman & Hall, 2004.
- MIichael I. Hartley, Alexander Hulpke. Polytopes derived from sporadic simple groups // Contributions to Discrete Mathematics. — 2010. — Т. 5, вип. 2 (3 березня). — С. 106-118. — ISSN 715-0868.