Граф призми

Окремі графи можна назвати за асоційованими тілами:

• Граф трикутної призми — 6 вершин, ребер 9
• Кубічний граф — 8 вершин, ребер 12
• Граф п'ятикутної призми — 10 вершин, ребер 15
• Граф шестикутної призми — 12 вершин, ребер 18
• Граф семикутної призми — 14 вершин, ребер 21
• Граф восьмикутної призми — 16 вершин, ребер 24
• …

Y3 = GP(3,1)

Y4 = Q3 = GP(4,1)

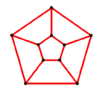Y5 = GP(5,1)

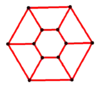Y6 = GP(6,1)

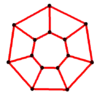Y7 = GP(7,1)

Y8 = GP(8,1)

Хоча геометрично зірчасті багатокутники також є гранями іншої послідовності (самоперетинних і неопуклих) призматичних багатогранників, графи цих зірчастих призм ізоморфні графам призм і не утворюють окремої послідовності графів.

Графи призм є прикладами узагальнених графів Петерсена з параметрами GP(n,1). Графи також можна утворити як прямий добуток циклу і одиничного ребра.

Як і багато вершинно-транзитивних графи, призматичні графи можна побудувати як граф Келі. Діедральна група порядку n є групою симетрій правильного n-кутника на площині. Вона діє на n-кутник обертаннями і відбиттями. Групу можна згенерувати двома елементами: обертанням на кут ${\displaystyle 2\pi /n}$ і одним відбиттям, і граф Келі цієї групи з цією генерувальною множиною є графом призми. Абстрактно група має задання ${\displaystyle \langle r,f\mid r^{n},f^{2},(rf)^{2}\rangle }$ (де r — це обертання, а f — відбиття) і граф Келі має генератори r і f (або r, r⁻¹ і f)[1].

Граф n-кутної призми з непарним n можна побудувати як циркулянтний граф ${\displaystyle C_{2n}^{2,n}}$, однак ця побудова не працює для парних значень n.

Граф n-кутної призми має 2n вершин і 3n ребер. Графи є регулярними кубічними графами. Оскільки призма має симетрії, які переводять будь-яку вершину в будь-яку іншу, графи призм є вершинно-транзитивними графами. Як поліедральні графи, ці графи також є вершинно 3-зв'язними планарними графами. Будь-який граф призми має гамільтонів цикл[2].

Серед усіх двозв'язних кубічних графів графи призм мають з точністю до сталого множника найбільше можливе число 1-розкладень графу. 1-розкладення — це розбиття множини ребер графу на три досконалих парування, або, еквівалентно, реберне розфарбування графу трьома кольорами. Будь-який двозв'язний кубічний граф з n вершинами має O(2^n/2) 1-розкладень, а граф призми має Ω(2^n/2) 1-розкладень[3].

Число кістякових дерев графу n-кутної призми задається формулою[4]:

${\displaystyle {\frac {n}{2}}{\bigl (}(2+{\sqrt {3}})^{n}+(2-{\sqrt {3}})^{n}){\bigr .}}$

Для n = 3, 4, 5, … ці числа рівні

78, 388, 1810, 8106, 35294, …

Графи n-кутних призм для парних n є частковими кубами. Вони утворюють одне з небагатьох відомих нескінченних сімейств кубічних графів часткових кубів, і вони є (за винятком чотирьох випадків) єдиними вершинно-транзитивними кубічними частковими кубами[5].

Граф п'ятикутної призми є одним із заборонених мінорів для графів з деревною шириною три[6]. Графи трикутної призми і куба мають деревну ширину рівно три, але всі великі призми мають деревну ширину чотири.

Інші нескінченні сімейства поліедральних графів, засновані подібним чином з багатогранників з правильними основами: графи антипризм і колеса (графи пірамід). Іншими вершинно-транзитивними поліедральними графами є архімедові графи.

Якщо два цикли призматичного графу розірвати видаленням одного ребра в одному і тому ж місці в обох циклах, отримаємо драбину. Якщо два видалених ребра замінити двома перехрещеними ребрами, отримаємо непланарний граф «драбина Мебіуса»[7].

• David Eppstein. The complexity of bendless three-dimensional orthogonal graph drawing // Journal of Graph Algorithms and Applications. — 2013. — Т. 17, вип. 1 (3 листопада). — С. 35–55. — DOI:10.7155/jgaa.00283.
• A. A. Jagers. A note on the number of spanning trees in a prism graph // International Journal of Computer Mathematics. — 1988. — Т. 24, вип. 2 (3 листопада). — С. 151–154. — DOI:10.1080/00207168808803639.
• Tilen Marc. Classification of vertex-transitive cubic partial cubes. — 2015. — 3 листопада. — arXiv:1509.04565.
• Stefan Arnborg, Andrzej Proskurowski, Derek G. Corneil. Forbidden minors characterization of partial 3-trees // Discrete Mathematics. — 1990. — Т. 80, вип. 1 (3 листопада). — С. 1–19. — DOI:10.1016/0012-365X(90)90292-P.
• Richard K. Guy, Frank Harary. On the Möbius ladders // Canadian Mathematical Bulletin. — 1967. — Т. 10 (3 листопада). — С. 493–496. — DOI:10.4153/CMB-1967-046-4.
• R. C. Read, R. J. Wilson. Chapter 6 special graphs // An Atlas of Graphs. — Oxford, England : Oxford University Press, 2004. — С. 261, 270.