Закон електромагнітної індукції Фарадея

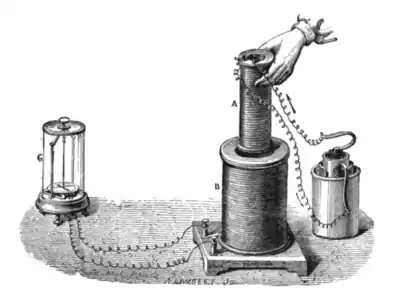
Електромагнітна індукція була виявлена незалежно один від одного Майклом Фарадеєм і Джозефом Генрі у 1831 році, проте Фарадей першим опублікував результати своїх експериментів[2][3].

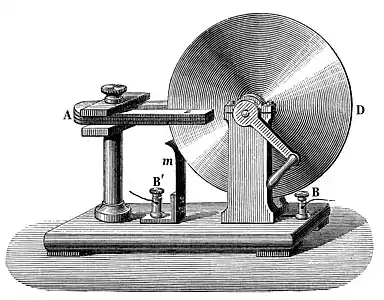
У першій експериментальній демонстрації електромагнітної індукції (серпень 1831) Фарадей обмотав двома проводами протилежні сторони залізного тора (конструкція схожа на сучасний трансформатор). Ґрунтуючись на своїй оцінці недавно виявленого властивості електромагніта, він очікував, що при включенні струму в одному проводі особливого роду хвиля пройде крізь тор і викличе деякий електричний вплив на його протилежний бік. Він підключив один провід до гальванометр у і дивився на нього, коли інший провід підключав до батареї. Справді, він побачив короткочасний сплеск струму (який він назвав «хвилею електрики»), коли підключав провід до батареї, і другий такий же сплеск, коли відключав його.[4] Протягом двох місяців Фарадей знайшов кілька інших проявів електромагнітної індукції. Наприклад, він побачив сплески струму, коли швидко вставляв магніт в котушку і витягав його назад, він генерував постійний струм в обертовому поблизу магніту мідному диску з ковзаючим електричним дротом («диск Фарадея»)[5].

Диск Фарадея

Фарадей пояснив електромагнітну індукцію з використанням концепції так званих силових ліній. Однак, більшість вчених того часу відхилили його теоретичні ідеї, в основному тому, що вони не були сформульовані математично.[6] Виняток склав Максвелл, який використовував ідеї Фарадея як основу для своєї кількісної електромагнітної теорії.[6][7][8] в роботах Максвелла аспект зміни в часі електромагнітної індукції виражений у вигляді диференціальних рівнянь. Олівер Хевісайд назвав це законом Фарадея, хоча він дещо відрізняється за формою від первинного варіанту закону Фарадея і не враховує індукування ЕРС при русі. Версія Хевисайда є формою визнаної сьогодні групи рівнянь, відомих як рівняння Максвелла.

Емілій Христіанович Ленц сформулював в 1834 році закон (правило Ленца), який описує «потік через ланцюг» і дає напрямок індукованої ЕРС і струму в результаті електромагнітної індукції.

Експеримент Фарадея, що показує індукцію між витками дроту: рідинна батарея (справа) дає струм, який протікає через невелику котушку (A) "", створюючи магнітне поле . Коли котушки нерухомі, струм не індукується. Але коли маленька котушка вставляється або вилучають із великою котушки (B) "", магнітний потік через котушку змінюється, викликаючи струм, який реєструється гальванометром (G) .[9]

Деякі фізики відзначають, що закон Фарадея в одному рівнянні описує два різних явища: 'рухову ЕРС' , генеровану дією магнітної сили на рухомий провід, і 'трансформаторну ЕРС' , генеровану дією електричної сили внаслідок зміни магнітного поля . Джеймс Клерк Максвелл звернув увагу на цей факт у своїй роботі Про фізичні силові лінії в 1861 році. У другій половині частини II цієї праці Максвелл дає окреме фізичне пояснення для кожного з цих двох явищ. Посилання на ці два аспекти електромагнітної індукції мається на деяких сучасних підручниках.[10] Як пише Річард Фейнман:[11]

Таким чином, «правило потоку» про те, що ЕРС в ланцюзі дорівнює швидкості зміни магнітного потоку через контур, застосовується незалежно від причини зміни потоку: чи то тому що поле змінюється, чи то тому що ланцюг рухається (або і те, і інше)... В нашому поясненні правила ми використовували два абсолютно різних закону для двох випадків - ${\displaystyle {\stackrel {\mathbf {v\times B} }{}}}$ для «рухомого ланцюга» і ${\displaystyle {\stackrel {\mathbf {\nabla \ x\ E\ =\ -\partial _{\ t}B} }{}}}$ для «мінливого поля».

Ми не знаємо ніякого аналогічного положення у фізиці, коли такі прості і точні загальні принципи вимагали б для свого реального розуміння аналізу з точки зору двох різних явищ.

— 'Річард Фейнман' , Фейнмановські лекції з фізики

Відображення цієї очевидної дихотомії було одним з основних шляхів, які привели Ейнштейна до розробки спеціальної теорії відносності:

Відомо, що електродинаміка Максвелла - як її зазвичай розуміють нині - при застосуванні до рухомих тіл призводить до асиметрії, яка, як здається, не притаманна цьому явищу. Візьмемо, приміром, електродинамічне взаємодія магніту і провідника. Спостережуване явище залежить тільки від відносного руху провідника і магніту, тоді як звичайне думка малює велика відмінність між цими двома випадками, в яких або одне, або інше тіло знаходиться в русі. Бо, якщо магніт знаходиться в русі, а провідник спочиває, в околиці магніту виникає електричне поле з певною щільністю енергії, створюючи струм там, де розташований провідник. Але якщо магніт покоїться, а провідник рухається, то в околиці магніту ніяке електричне поле не виникає. У провіднику, проте, ми знаходимо електрорушійну силу, для якої не існує відповідної енергії самої по собі, але яка викликає - припускаючи рівність відносного руху в двох обговорюваних випадках - електричні струми по тому ж напрямку і тій же інтенсивності, як у першому випадку.

Приклади подібного роду разом з невдалою спробою виявити який-небудь рух Землі щодо «світлоносного середовища» припускають, що явища електродинаміки, а також механіки не володіють властивостями, відповідними ідеї абсолютного спокою.

— 'Альберт Ейнштейн' , До електродинаміки рухомих тіл [12]

Визначення поверхневого інтеграла припускає, що поверхня Σ поділена на дрібні елементи. Кожен елемент пов'язаний з вектором d 'A' , величина якого дорівнює площі елемента, а напрям — по нормалі до елемента у зовнішню сторону.

Векторне поле 'F' ( 'r' , t ) визначено у всьому просторі, а поверхню Σ обмежена кривою ∂Σ, що рухається зі швидкістю 'v' . З цієї поверхні виробляється інтегрування поля.

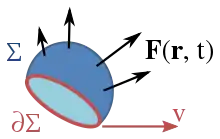
Закон електромагнітної індукції Фарадея використовує поняття магнітного потоку Φ _B через замкнуту поверхню Σ, який визначений через поверхневий інтеграл:

${\displaystyle \Phi _{B}=\iint \limits _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,t)\cdot d\mathbf {A} ,}$

де d A — площа елемента поверхні Σ ( t ), B — магнітне поле, а B · d A - скалярний добутокBіd A. Передбачається, що поверхня має «гирло», окресленої замкнутої кривої, позначеної ∂Σ ( t ). Закон індукції Фарадея стверджує, що коли потік змінюється, то при переміщенні одиничного позитивного пробного заряду по замкнутій кривій ∂Σ відбувається робота ${\displaystyle {\mathcal {E}}}$, величина якої визначається за формулою:

${\displaystyle |{\mathcal {E}}|=\left|{{d\Phi _{B}} \over dt}\right|,}$

де ${\displaystyle |{\mathcal {E}}|}$ — величина електрорушійної сили (ЕРС) в вольтах, а Φ _B  — магнітний потік в веберах. Напрямок електрорушійної сили визначається законом Ленца.

Для щільно намотаною котушки індуктивності, яка містить N витків, кожен з однаковим магнітним потоком Φ _B , закон індукції Фарадея стверджує, що:

${\displaystyle |{\mathcal {E}}|=N\left|{{d\Phi _{B}} \over dt}\right|}$

де N — число витків проводу, Φ _B  — магнітний потік в веберах на один виток.

При виборі шляху ∂Σ ( t ) для знаходження ЕРС зауважимо, що шлях повинен задовольняти двом основним вимогам: (i) шлях повинен бути замкнутим, і (ii) шлях повинен охоплювати відносний рух частин контуру (джерело походження t -залежності в ∂Σ ( t )). До вимог не відноситься те, що шлях повинен збігатися з лінією струму, але, звичайно, ЕРС, яка знаходиться за законом потоку, вважатиметься обраним шляхом. Якщо шлях не збігається з лінією струму, то підрахована ЕРС, можливо, буде не та ЕРС, яка викликає струм.

Мал. 3. Замкнутий прямокутний провід рухається уздовж осі x зі швидкістю 'v' в магнітному полі, яке змінюється в уздовж x .

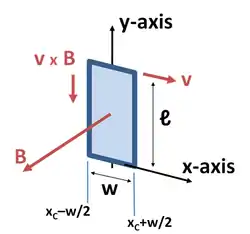
Розглянемо випадок на малюнку 3, на якому прямокутна замкнута дротова петля, розташована в площині xy , переміщується в напрямку осі x зі швидкістю v . Центр петлі x _C задовольняє умові v = dx _C / dt . Петля має довжину ℓ в напрямку осі y і ширину w в напрямку осі x . Залежне від часу просторово мінливий магнітне поле B ( x ) показано в напрямку z . Магнітне поле на лівій стороні одно B ( x _C  — w / 2 ), а на правій стороні B ( x _C + w / 2 ). Електрорушійну силу можна знайти або за допомогою закону Лоренца, або, що еквівалентно, використовуючи вищевикладений закон індукції Фарадея.

Рис. 4. Замкнуте прямокутний провід обертається з кутовий швидкістю ω в радіальному, направленому назовні магнітному полі 'B' фіксованої величини. Струм знімається щітками, що стосуються верхнього і нижнього дисків з провідними ободами.

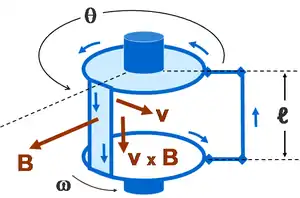
На рис. 4 показаний шпиндель, утворений двома дисками з які проводять ободами, і провідна петля, розташована вертикально між цими ободами. Ця конструкція обертається в магнітному полі, яке спрямоване радіально назовні і має одне і те ж значення в будь-якому напрямку. Радіально орієнтований колекторний зворотний контур на кінцях петлі знімає струм з провідних поверхонь ободів. Розташування колекторного зворотного контуру по відношенню до поля 'B' таке, що поле має напрямок у площині цього колекторного контуру, тому сам він не вносить ніякого додаткового потоку в ланцюг. Електрорушійну силу можна знайти безпосередньо за допомогою вищевикладеного закону Фарадея.

Пряма оцінка зміни потоку

Мал. 5. Спрощена версія рис. 4. Петля ковзає зі швидкістю 'v' в стаціонарному однорідному полі 'B' .

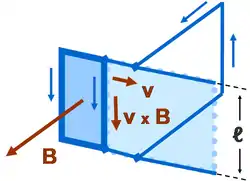
Використання замкнутого шляху для обчислення ЕРС, як це зроблено вище, залежить від детальної геометрії шляху. На відміну від цього, використання закону Лоренца не залежить від таких обмежень. Нижченаведене розгляд призначено для кращого розуміння еквівалентності шляхів і дозволить уникнути з'ясування деталей обраного шляху при використанні закону потоку.

Рис.5 є ідеалізацією малюнка 4, тут зображена проекція циліндра на площину. Дійсний той самий аналіз по зв'язаному шляху, але зроблені деякі спрощення. Не залежні від часу деталі ланцюга не можуть впливати на швидкість зміни потоку. Наприклад, при постійній швидкості ковзання петлі, протікання струму через петлю не залежить від часу. замість того, щоб при обчисленнях ЕРС розглядати деталі обраного замкнутого контуру, можна зосередитися на області поля 'B' , замітають рухомій петлей. Предложеніе зводиться до знаходження швидкості, з якою потік перетинає ланцюг.[15] Це поняття забезпечує пряму оцінку швидкості зміни потоку, що дозволяє не замислюватися про більш залежних від часу деталях різних варіантів шляху по цепі. Так ж, як при застосуванні закону Лоренца, стає ясно, що два будь шляху, пов'язаних з ковзаючою петлею, але відрізняються тим, яким чином вони перетинають петлю, створюють потік з такою ж швидкістю його зміни.

На рис.5 область замітання в одиницю часу дорівнює dA / dt = v ℓ, незалежно від деталей обраного замкнутого шляху, так що за законом індукції Фарадея ЕРС дорівнює:[16]

${\displaystyle {\mathcal {E}}={{d\Phi _{B}} \over dt}=Bv\ell \ .}$

Цей шлях незалежної ЕРС показує, що якщо змінна петля замінена твердої провідної пластиною або навіть деякої складної викривленої поверхнею, аналіз буде такою ж: знайти потік в замітає області рухомі частини ланцюга. Аналогічним чином, якщо ковзна петля в барабані генератора на рис. 4 замінюється на твердий провідний циліндр, розрахунок замітає площі робиться точно так же, як і у випадку з простою петлею. Тобто ЕРС, обчислена за законом Фарадея, буде точно така ж, як у випадку циліндра з твердими провідними стінками, або, якщо хочете, циліндра із стінками з тертого сиру. Зауважимо, однак, що струм, що протікає в результаті цієї ЕРС, не буде точно таким же, тому що струм залежить ще від опору ланцюга.

Мал. 6. Ілюстрація теореми Кельвіна-Стокса за допомогою поверхні Σ, її кордони ∂Σ і орієнтації n, встановленої правилом правої руки.

Змінне магнітне поле створює електричне поле, що описується рівнянням Фарадея — Максвелла:

де:

${\displaystyle \nabla \times }$ позначає ротор

E — електричне поле

B — щільність магнітного потоку.

Це рівняння присутній в сучасній системі рівнянь Максвелла, часто його називають законом Фарадея. Однак, оскільки воно містить тільки частинні похідні за часом, його застосування обмежене ситуаціями, коли заряд покоїться в змінному за часом магнітному полі. Воно не враховує електромагнітну індукцію у випадках, коли заряджена частинка рухається в магнітному полі.

В іншому вигляді закон Фарадея може бути записаний через інтегральну форму теореми Кельвіна-Стокса:[17]

${\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\partial \over {\partial t}}\mathbf {B} \cdot d\mathbf {A} }$

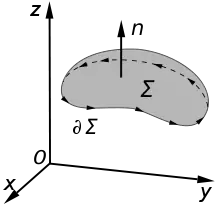
Для виконання інтегрування потрібно незалежна від часу поверхню Σ (розглянута в даному контексті як частина інтерпретації частинних похідних). Як показано на рис. 6:

Σ — поверхня, обмежена замкнутим контуром ∂Σ, причому, як Σ, так і ∂Σ є фіксованими, не залежними від часу,

E — електричне поле,

D ℓ — нескінченно малий елемент контуру ∂Σ,

B — магнітне поле,

D A — нескінченно малий елемент вектора поверхні Σ.

Елементи d ℓ і d A мають невизначені знаки. Щоб встановити правильні знаки, використовується правило правої руки, як описано в статті про теоремі Кельвіна-Стокса. Для плоскої поверхні Σ позитивний напрямок елемента шляху d ℓ кривої ∂Σ визначається правилом правої руки, за яким на цей напрям вказують чотири пальці правої руки, коли великий палець вказує в напрямку нормалі n до поверхні Σ.

Інтеграл по ∂Σ називається інтеграл по шляху або криволінійним інтегралом . Поверхневий інтеграл в правій частині рівняння Фарадея-Максвелла є явним виразом для магнітного потоку Φ _B через Σ. Зверніть увагу, що ненульовий інтеграл по шляху для E відрізняється від поведінки електричного поля, створюваного зарядами. Генероване зарядом E — поле може бути виражено як градієнт скалярного поля, яке є рішенням рівняння Пуассона і має нульовий інтеграл по шляху.

Інтегральне рівняння справедливо для будь-якого шляху ∂Σ в просторі і будь-якій поверхні Σ, для якої цей шлях є кордоном. <! — Однак слід зазначити, що в цій формулі ∂Σ і Σ розуміються як не залежними від часу. Ця інтегральна форма не може ставитися до рухової ЕРС, бо Σ не залежить від часу. Зверніть також увагу, що це рівняння не має посилання на ЕРС ${\displaystyle {\overset {\mathcal {E}}{}}}$, & thinsp, та й не може її мати без введення сили Лоренца, що дозволяє провести обчислення роботи.- ->

Мал. 7. Площа замітання елемента вектора d ℓ кривої ∂Σ за час dt при русі зі швидкістю v.

Використовуючи повну силу Лоренца для розрахунку ЕРС,

${\displaystyle {\mathcal {E}}=\oint _{\partial \Sigma (t)}\left(\mathbf {E} (\mathbf {r} ,t)+\mathbf {v\times B} (\mathbf {r} ,t)\right)\cdot d{\boldsymbol {\ell }},}$

заяву закон індукції Фарадея більш загальним, ніж інтегральна форма рівнянь Максвелла-Фарадея рівняння (див. Лоренца сила): a statement of Faraday's law of induction more general than the integral form of the Maxwell-Faraday equation is (see Lorentz force):

${\displaystyle \oint _{\partial \Sigma (t)}\left(\mathbf {E} (\mathbf {r} ,t)+\mathbf {v\times B} (\mathbf {r} ,t)\right)\cdot d{\boldsymbol {\ell }}\ }$ ${\displaystyle \ =-{\frac {d}{dt}}\iint _{\Sigma (t)}d{\boldsymbol {A}}\cdot \mathbf {B} (\mathbf {r} ,\ t)\,}$

де ∂ Σ (T) є замкнутою траєкторії переміщення обмежує рухомої поверхні Σ (T), а V-швидкість руху. Див. Рисунок 2. Зверніть увагу, що звичайна похідна за часом використовується, а не часткова похідна часу, що означає зміну в часі Σ (T) повинні бути включені в диференціації. В підінтегральний елемент крива г ℓ рухається зі швидкістю v. Використовуючи[18]

${\displaystyle {\frac {\text{d}}{{\text{d}}t}}\int \limits _{A}{\mathbf {B} }{\text{ d}}\mathbf {A} =\int \limits _{A}{\left({\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {v} \ {\text{div}}\ \mathbf {B} +{\text{curl}}\;(\mathbf {B} \times \mathbf {v} )\right)\;{\text{d}}}\mathbf {A} }$

і враховуючи ${\displaystyle {\text{div}}\mathbf {B} =0}$ (Ряд Гаусса), ${\displaystyle \mathbf {B} \times \mathbf {v} =-\mathbf {v} \times \mathbf {B} }$ і беручи до уваги ${\displaystyle {\text{div}}\mathbf {B} =0}$ (Ряд Гаусса), ${\displaystyle \mathbf {B} \times \mathbf {v} =-\mathbf {v} \times \mathbf {B} }$ (Векторний добуток) і ${\displaystyle \int _{A}{\text{curl}}\;\mathbf {X} \;\mathrm {d} \mathbf {A} =\oint _{\partial A}\mathbf {X} \;{\text{d}}{\boldsymbol {\ell }}}$ (теорема Кельвіна — Стокса), ми знаходимо, що повна похідна магнітного потоку може бути виражена

${\displaystyle \int \limits _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}{\textrm {d}}\mathbf {A} ={\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{d}}\mathbf {A} +\oint _{\partial \Sigma }\mathbf {v} \times \mathbf {B} \,{\text{d}}{\boldsymbol {\ell }}}$

Додаючи член ${\displaystyle \oint \mathbf {v} \times \mathbf {B} \mathrm {d} \mathbf {\ell } }$ до обох частин рівняння Фарадея-Максвелла і вводячи вищенаведене рівняння, ми отримуємо:

${\displaystyle \oint \limits _{\partial \Sigma }{(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}{\text{d}}\ell =\underbrace {-\int \limits _{\Sigma }{\frac {\partial }{\partial t}}\mathbf {B} {\text{d}}\mathbf {A} } _{{\text{induced}}\ {\text{emf}}}+\underbrace {\oint \limits _{\partial \Sigma }{\mathbf {v} }\times \mathbf {B} {\text{d}}\ell } _{{\text{motional}}\ {\text{emf}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{d}}\mathbf {A} ,}$

що і є законом Фарадея. Таким чином, закон Фарадея і рівняння Фарадея-Максвелла фізично еквівалентні.

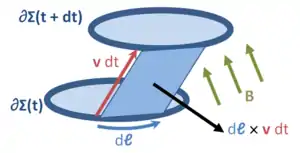
Мал.7 показує інтерпретацію вкладу магнітної сили в ЕРС у лівій частині рівняння. Площа, що замітається сегментом d ℓ кривої ∂Σ за час dt при русі зі швидкістю v, дорівнює:

${\displaystyle d\mathbf {A} =-d{\boldsymbol {\ell \times v}}dt\,}$

так що зміна магнітного потоку ΔΦ _B через частину поверхні, обмеженої ∂Σ за час dt, одна:

${\displaystyle {\frac {d\Delta \Phi _{B}}{dt}}=-\mathbf {B} \cdot \ d{\boldsymbol {\ell \times v}}\ =-\mathbf {v} \times \mathbf {B} \cdot \ d{\boldsymbol {\ell }}\,}$

і якщо скласти ці ΔΦ _B -вклади навколо петлі для всіх сегментів d ℓ, ми отримаємо сумарний вклад магнітної сили в закон Фарадея. Тобто цей термін пов'язаний з руховою ЕРС.

Мал. 8. Електричний генератор на основі диска Фарадея. Диск обертається з кутовий швидкістю ω, при цьому провідник, розташований уздовж радіуса, рухається в статичному магнітному полі B. Магнітна сила Лоренца v × B створює струм вздовж провідника за напрямом до обода, потім ланцюг замикається через нижню щітку і вісь підтримки диска. Таким чином, внаслідок механічного руху генерується струм.

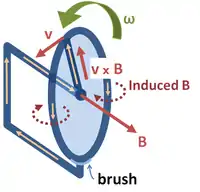
Явище виникнення ЕРС, породженої за законом індукції Фарадея через відносного руху контуру і магнітного поля, лежить в основі роботи електричних генераторів. Якщо постійний магніт переміщається щодо провідника або навпаки, провідник переміщається щодо магніту, то виникає електрорушійна сила. Якщо провідник підключений до електричної навантаженні, то через неї буде текти струм, і отже, механічна енергія руху перетворюватиметься на електричну енергію. Наприклад, дисковий генератор побудований за тим же принципом, як зображено на рис. 4. Інший реалізацією цієї ідеї є диск Фарадея, показаний в спрощеному вигляді на рис. 8. Зверніть увагу, що і аналіз рис. 5, і пряме застосування закону сили Лоренца показують, що твердий проводить диск працює однаковим чином.

У прикладі диска Фарадея диск обертається в однорідному магнітному полі, перпендикулярному диску, в результаті чого виникає струм в радіальному плечі завдяки силі Лоренца. Цікаво зрозуміти, як виходить, що щоб управляти цим струмом, необхідна механічна робота. Коли генерований струм тече через провідний обід, по закону Ампера цей струм створює магнітне поле (на рис. 8 вона підписана «індуковане B» — Induced B). Обод, таким чином, стає електромагніт ом, який чинить опір обертанню диска (приклад правила Ленца). В дальній частині малюнка зворотний струм тече від обертового плеча через дальню сторону обода до нижньої щітці. Поле В, створюване цим зворотним струмом, протилежно прикладеному полю, викликаючи скорочення потоку через дальню сторону ланцюга, на противагу збільшенню потоку, викликаного обертанням. На ближній стороні малюнка зворотний струм тече від обертового плеча через ближню сторону обода до нижньої щітці. Індуковане поле B збільшує потік по цю сторону ланцюга, на противагу зниженню потоку, викликаного обертанням. Таким чином, обидві сторони ланцюга генерують ЕРС, що перешкоджає обертанню. Енергія, необхідна для підтримки руху диска на противагу цій реактивної силі, в точності дорівнює вироблюваної електричної енергії (плюс енергія на компенсацію втрат через тертя, через виділення тепла Джоуля та інше). Така поведінка є загальним для всіх генераторів перетворення механічної енергії в електричну.

Хоча закон Фарадея описує роботу будь-яких електричних генераторів, детальний механізм в різних випадках може відрізнятися. Коли магніт обертається навколо нерухомого провідника, мінливий магнітне поле створює електричне поле, як описано в рівнянні Максвелла-Фарадея, і це електричне поле штовхає заряди через провідник. Цей випадок називається індукованої ЕРС. З іншого боку, коли магніт нерухомий, а провідник обертається, на рухомі заряди впливає магнітна сила (як описується законом Лоренца), і ця магнітна сила штовхає заряди через провідник. Цей випадок називається рухової ЕРС.[21]

Електричний генератор може працювати в «зворотному напрямку» і ставати двигуном. Розглянемо, наприклад, диск Фарадея. Припустимо, постійний струм тече через яке проводить радіальне плече від будь-якого напруження. Тоді за законом сили Лоренца на цей рухомий заряд впливає сила в магнітному полі B, яка буде обертати диск у напрямку, певним правилом лівої руки. За відсутності ефектів, що викликають дисипативні втрати, таких як тертя або тепло Джоуля, диск буде обертатися з такою швидкістю, щоб d ΦB/dt дорівнювало напрузі, що породжує струм.

ЕРС, передвіщена законом Фарадея, є також причиною роботи електричних трансформаторів. Коли електричний струм в дротяній петлі змінюється, мінливий струм створює змінне магнітне поле. Другий провід в доступному для нього магнітному полі буде відчувати ці зміни магнітного поля як зміни пов'язаного з ним магнітного потоку d ΦB / d t. Електрорушійна сила, що виникає в другій петлі, називається індукованої ЕРС або ЕРС трансформатора. Якщо два кінця цієї петлі зв'язати через електричну навантаження, то через неї потече струм.

Закон Фарадея використовується для вимірювання витрати електропровідних рідин і суспензій. Такі прилади називаються магнітними витратомірам. Наведене напруга ℇ, що генерується в магнітному полі B за рахунок провідної рідини, що рухається зі швидкістю v , визначається за формулою:

${\displaystyle {\mathcal {E}}=B\ell v,}$

де ℓ — відстань між електродами в магнітному витратомірі.

У будь-якому металевому об'єкті, рухомому по відношенню до статичного магнітному полю, виникатимуть індукційні струми, як і в будь-якому нерухомому металевому предметі по відношенню до рухомого магнітному полю. Ці енергетичні потоки найчастіше небажані, через них в шарі металу тече електричний струм, який нагріває метал.

Є ряд методів, використовуваних для боротьби з цими небажаними індуктивними ефектами.

• Електромагніти в електричних двигунах, генераторах і трансформаторах не роблять із суцільного металу, а використовують тонкі листи жерсті, звані «ламінатами». Ці тонкі пластини зменшують паразитні вихрові струми, як буде описано нижче.
• Котушки індуктивності в електроніці зазвичай використовують магнітні сердечники, щоб мінімізувати паразитний струм. Їх роблять з суміші металевого порошку зі сполучною наповнювачем, і вони мають різну форму. Сполучний матеріал запобігає проходженню паразитних струмів через порошковий метал.

Розшарування електромагніта

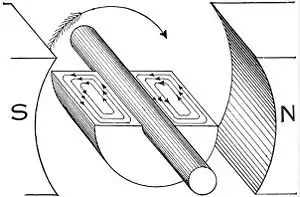
Вихрові струми виникають, коли суцільна маса металу обертається в магнітному полі, так як зовнішня частина металу перетинає більше силових ліній, ніж внутрішня, отже, iндукцiйна електрорушійна сила нерівномірна і прагне створити струми між точками з найбільшим і найменшим потенціалами. Вихрові струми споживають значну кількість енергії, і часто призводять до шкідливого підвищення температури.[22]

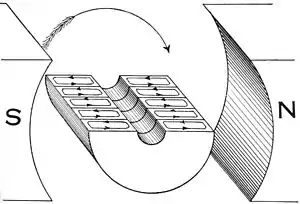
На цьому прикладі показані всього п'ять ламинатiв або пластин для демонстрації розщеплення вихрових струмів. На практиці число пластин або перфорацій складає від 40 до 66 на дюйм, що призводить до зниження втрат на вихрових токах приблизно до одного відсотка. Хоча пластини можуть бути відокремлені одна від одної ізоляцією, але оскільки виникаючі напруги надзвичайно низькі, то природної іржі або оксидного покриття пластин достатньо для того, щоб запобігти струм через пластини.[22]

Це ротор від двигуна постійного струму діаметром приблизно 20 мм, використовуваного в програвачах компакт-дисків. Зверніть увагу, для зниження паразитних індуктивних втрат зроблено розшарування полюса електромагніта на частини.

Паразитні втрати в котушках індуктивності

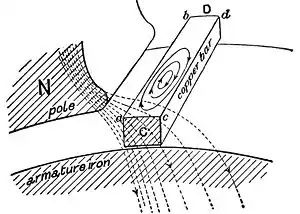
На цій ілюстрації суцільний мідний стрижень котушки індуктивності в обертовому якорі просто проходить під кінчиком полюса N магніту. Зверніть увагу на нерівномірний розподіл силових ліній через стрижень. Магнітне поле має велику концентрацію і, отже, сильніше на лівому краю мідного стержня (a, b), тоді як слабше по правому краю (c, d). Оскільки два краю стержня рухатимуться з однаковою швидкістю, це розходження в напруженості поля через стрижень створить вихори струму всередині мідного стержня.[23]

Це одна з причин, по якій пристрої з високою напругою, як правило, більш ефективні, ніж низьковольтні пристрої. Високовольтні пристрої мають безліч невеликих витків дроту в двигунах, генераторах і трансформаторах. Ці численні невеликі витки проводу в електромагніті розбивають вихрові потоки, а в межах великих, товстих котушок індуктивності низької напруги утворюється вихрові струми більшої величини.

• A simple interactive Java tutorial on electromagnetic induction
• R. Vega Induction: Faraday's law and Lenz's law — Highly animated lecture
• Notes from Physics and Astronomy HyperPhysics at Georgia State University
• Faraday's Law for EMC Engineers
• James Clerk (1881), A treatise on electricity and magnetism, Vol.II, Chapter III, § 530, p. 178. Oxford, UK: Clarendon Press.ISBN 0-486-60637-6.
• Tankersley and Mosca: Introducing Faraday's law.