Логічні елементи

Логічні операції (булева функція) своє теоретичне обґрунтування отримали в математичній логіці.

Логічні операції з одним операндом називаються унарними, з двома — бінарними, з трьома — тернарними і т. д.

Із ${\displaystyle 2^{(2^{1})}=2^{2}=4}$ можливих унарних операцій з унарним виходом інтерес для реалізації представляють операції заперечення і повторення, причому, операція заперечення має більше значення, ніж операція повторення, так як повторювач може бути зібраний з двох інверторів, а інвертор з повторювачів не зібрати.

Заперечення. Операція "НЕ"

Інвертор, НЕ (IEC)

Інвертор, НЕ (ANSI)

${\displaystyle A}$	${\displaystyle -A}$
0	1
1	0

Мнемонічне правило для НЕ звучить так:

На виході буде:

• «1» тоді і лише тоді, коли на вході «0»,

• «0» тоді і лише тоді, коли на вході «1»

Повторення

Повторювач

${\displaystyle A}$	${\displaystyle A}$
0	0
1	1

Перетворення інформації вимагає виконання операцій з групами знаків, найпростішої з яких є група з двох знаків. Оперування з великими групами завжди можна розбити на послідовні операції з двома знаками.

Із ${\displaystyle 2^{(2^{2})}=2^{4}=16}$ можливих бінарних логічних операцій з двома знаками та унарним виходом. Інтерес для реалізації представляють 10 операцій, наведених нижче.

Кон'юнкція. Операція "І"

І (IEC)

І (ANSI)

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle A\land B}$
0	0	0
1	0	0
0	1	0
1	1	1

Логічний елемент, який реалізує функцію кон'юнкції, називається схемою збігу. Мнемонічне правило для І з будь-якою кількістю входів звучить так: На виході буде:

• «1» тоді і тільки тоді, коли на всіх входах діють «1»,
• «0» тоді і тільки тоді, коли хоча б на одному вході діє «0»

Словесно цю операцію можна виразити таким виразом: "Істина на виході може бути при істині на вході 1 та істині на вході 2".

Диз'юнкція. Операція "АБО"

АБО (IEC)

АБО (ANSI)

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle B\lor A}$
0	0	0
1	0	1
0	1	1
1	1	1

Мнемонічне правило для АБО з будь-якою кількістю входів звучить так: На виході буде:

• «1» тоді і тільки тоді, коли хоча б на одному вході діє «1»,
• «0» тоді і тільки тоді, коли на всіх входах діють «0»

Заперечення кон'юнкції. Операція "І-НЕ" (штрих Шефера)

І-НЕ (IEC)

І-НЕ (ANSI)

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle A|B}$
0	0	1
0	1	1
1	0	1
1	1	0

Мнемонічне правило для І-НЕ з будь-якою кількістю входів звучить так: На виході буде:

• «1» тоді і тільки тоді, коли хоча б на одному вході діє «0»,
• «0» тоді і тільки тоді, коли на всіх входах діють «1»

Заперечення диз'юнкції. Операція "АБО-НЕ" (стрілка Пірса)

В англомовній літературі NOR.

АБО-НЕ (IEC)

АБО-НЕ (ANSI)

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle A}$↓${\displaystyle B}$
0	0	1
0	1	0
1	0	0
1	1	0

Мнемонічне правило для АБО-НЕ з будь-якою кількістю входів звучить так: На виході буде:

• «1» тоді і тільки тоді, коли на всіх входах діють «0»,
• «0» тоді і тільки тоді, коли хоча б на одному вході діє «1»

Еквіваленція. Операція "ВИКЛЮЧНЕ_АБО-НЕ"

ВИКЛ._АБО-НЕ (IEC)

ВИКЛ._АБО-НЕ (ANSI)

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle A}$↔${\displaystyle B}$
0	0	1
0	1	0
1	0	0
1	1	1

Мнемонічне правило ВИКЛЮЧНЕ_АБО-НЕ з будь-якою кількістю входів звучить так: На виході буде:

• «1» тоді і тільки тоді, коли на вході діє парна кількість,
• «0» тоді і тільки тоді, коли на вході діє непарна кількість

Словесний опис: "істина на виході при істині на вході 1 і вході 2 або при хибності на вході 1 і вході 2".

Виключна диз'юнкція. Операція ВИКЛЮЧНЕ_АБО

ВИКЛ._АБО (IEC)

ВИКЛ._АБО (ANSI)

В англомовній літературі XOR (від англ. eXclusive OR).

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle f(AB)}$
0	0	0
0	1	1
1	0	1
1	1	0

Мнемонічне правило для ВИКЛЮЧНЕ_АБО з будь-якою кількістю входів звучить так: На виході буде:

• «1» тоді і тільки тоді, коли на вході діє непарна кількість,
• «0» тоді і тільки тоді, коли на вході діє парна кількість

Словесний опис: «істина на виході — тільки при істині на вході 1, або тільки при істині на вході 2».

Імплікація

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle A}$→${\displaystyle B}$
0	0	1
0	1	1
1	0	0
1	1	1

Мнемонічне правило для імплікації звучить так: На виході буде:

• «0» тоді і тільки тоді, коли на «B» менше «А»,
• «1» тоді і тільки тоді, коли на «B» більше або дорівнює «А»

Обернена імплікація

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle B}$→${\displaystyle A}$
0	0	1
0	1	0
1	0	1
1	1	1

Мнемонічне правило для оберненої імплікації звучить так: На виході буде:

• «0» тоді і тільки тоді, коли на «B» більше «А»,
• «1» тоді і тільки тоді, коли на «B» менше або дорівнює «А»

Декремент

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle f(A,B)}$
0	0	0
0	1	0
1	0	1
1	1	0

Мнемонічне правило для декременту від A до B звучить так: На виході буде:

• «1» тоді і тільки тоді, коли на «A» більше «B»,
• «0» тоді і тільки тоді, коли на «A» менше або дорівнює «B»

Інкремент

${\displaystyle A}$	${\displaystyle B}$	${\displaystyle f(A,B)}$
0	0	0
0	1	1
1	0	0
1	1	0

Мнемонічне правило для інкременту звучить так: На виході буде:

• «1» тоді і тільки тоді, коли на «B» більше «A»,
• «0» тоді і тільки тоді, коли на «B» менше або дорівнює «A»

Цими найпростішими логічними операціями (функціями), і навіть деякими їх підмножинами, можна висловити будь-які інші логічні операції. Такий набір найпростіших функцій називається функціонально повним логічним базисом. Таких базисів 4:

• І, НЕ (2 елемента)
• АБО, НЕ (2 елемента)
• І-НЕ (1 елемент)
• АБО-НЕ (1 елемент).

Для перетворення логічних функцій в один з названих базисів необхідно застосовувати правила де Моргана.

Реалізація логічних елементів можлива за допомогою пристроїв, що використовують найрізноманітніші фізичні принципи:

• Механічні,
• Гідравлічні,
• Пневматичні,
• Електромагнітні,
• Електромеханічні,
• Електронні.

Фізичні реалізації однієї і тієї ж логічної функції, а також позначення для істини і хибності, в різних системах електронних і не електронних елементів відрізняються один від одного.

Логічні елементи підрозділяються і за типом використаних в них електронних елементів. Найбільше застосування в даний час знаходять такі логічні елементи:

• РТЛ (резисторно-транзисторна логіка)
• ДТЛ (діодно-транзисторна логіка)
• ТТЛ (транзисторно-транзисторна логіка)

Спрощена схема двовхідного елемента І-НЕ ТТЛ .

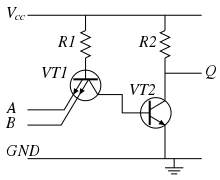
Зазвичай вхідний каскад логічних елементів ТТЛ являє собою найпростіший компаратор, який може бути виконаний різними способами (на багатоемітерному транзисторі або на діодній збірці). У логічних елементах ТТЛ вхідний каскад, окрім функцій компараторів, виконує і логічні функції. Далі слідує вихідний підсилювач з двотактним (двоключовим) виходом.

У логічних елементах КМОН вхідні каскади також являють собою найпростіші компаратори. Підсилювачами є КМОН-транзистори. Логічні функції виконуються комбінаціями паралельно і послідовно включених ключів, Які одночасно є і вихідними ключами.

Транзистори можуть працювати в інверсному режимі, але з меншим коефіцієнтом посилення. Ця властивість використовуються в ТТЛ багатоемітерних транзисторах. При подачі на обидва входи сигналу високого рівня (1,1) перший транзистор виявляється включеним в інверсному режимі за схемою емітерного повторювача з високим рівнем на базі, транзистор відкривається і підключає базу другого транзистора до високого рівня, струм йде через перший транзистор в базу другого транзистора і відкриває його. Другий транзистор «відкритий», його опір малий і на його колекторі напруга відповідає низькому рівню (0). Якщо хоча б на одному з входів сигнал низького рівня (0), тоді транзистор опиняється увімкненим за схемою із загальним емітером, через базу першого транзистора на цей вхід йде струм, що відкриває його і він замикає базу другого транзистора на землю, напруга на базі другого транзистора мала і він «закритий», вихідна напруга відповідає високому рівню. Таким чином, таблиця істинності відповідає функції 2І-НЕ.

• ТТЛШ (з діодами Шотткі)

Для збільшення швидкодії логічних елементів в них використовуються транзистори Шотткі (транзистори з діодами Шотткі), відмінною рисою яких є застосування в їхній конструкції випрямляючого контакту метал-напівпровідник замість p-n переходу. При роботі цих приладів відсутня інжекція неосновних носіїв та явища накопичення та розсмоктування заряду, що забезпечує високу швидкодію. Включення цих діодів паралельно колекторного переходу блокує насичення вихідних транзисторів, що збільшує напругу логічних 0 та 1, але зменшує втрати часу на перемикання логічного елемента при тому ж споживанні струму (або дозволяє зменшити споживаний струм при збереженні стандартної швидкодії). Так, серія 74хх і серія 74LSxx мають приблизно рівну швидкодію (насправді, серія 74LSxx дещо швидша), але споживаний від джерела живлення струм менший в 4-5 разів (у стільки ж разів менший і вхідний струм логічного елемента).

• КМОН (логіка на основі МДН-транзисторів)
• ЕЗЛ (емітерно-зв'язана логіка)

Ця логіка, інакше звана логікою на перемикачах струму, побудована на базі біполярних транзисторів, об'єднаних в диференціальні каскади. Один із входів зазвичай підключений усередині мікросхеми до джерела опорної (зразкової) напруги, приблизно посередині між логічними рівнями. Сума струмів через транзистори диференціального каскаду постійна, в залежності від логічного рівня на вході змінюється лише те, через який з транзисторів тече цей струм. На відміну від ТТЛ, транзистори в ЕЗЛ працюють в активному режимі і не входять до насичення або в інверсний режим. Це призводить до того, що швидкодія ЕЗЛ-елемента при тій же технології (тих же характеристиках транзисторів) набагато більша, ніж ТТЛ-елемента, але більший і споживаний струм. До того ж, різниця між логічними рівнями у ЕЗЛ-елемента набагато менша, ніж у ТТЛ (менше вольта), і, для прийнятної завадостійкості, доводиться використовувати негативну напругу живлення (а іноді і застосовувати для вихідних каскадів друге живлення). Зате максимальні частоти перемикання тригерів на ЕЗЛ більш ніж на порядок перевищують можливості сучасних їм ТТЛ, наприклад, серія К500 забезпечувала частоти перемикання 160-200 МГц, в порівнянні з 10-15 МГц сучасної їй ТТЛ серії К155. В даний час і ТТЛ (Ш), і ЕЗЛ практично не використовуються, оскільки зі зменшенням проектних норм КМОН-технологія досягла частот перемикання в кілька гігагерц.

Логічні елементи входять до складу мікросхем, наприклад ТТЛ елементи - до складу мікросхем К155 (SN74), К133; ТТЛШ - 530, 533, К555, ЕЗЛ - 100, К500 і т. д.

Комбінаційними називаються такі логічні пристрої, вихідні сигнали котрих однозначно визначаються вхідними сигналами:

• Суматор
• Напівсуматор
• Шифратор
• Дешифратор
• Мультиплексор
• Демультиплексор
• Цифровий компаратор
• Мажоритарний елемент
• Постійний запам'ятовувач як універсальна комбінаційна логічна схема

Всі вони виконують найпростіші двійкові, трійкові або n-кові логічні функції.

Послідовними називають такі логічні пристрої, вихідні сигнали яких визначаються не тільки сигналами на входах, а й передісторією їх роботи, тобто станом елементів пам'яті.

• Тригер
• Лічильник імпульсів
• Регістр
• Вен'юнктор
• Секвентор

• Бітові операції
• Булева функція
• Алгебра логіки
• Комбінаційна логіка
• Секвенційна логіка

• Элементы и узлы цифровых электронных приборов. Логические элементы.(рос.)

• Новиков Ю. В. Введение в цифровую схемотехнику. Курс лекций. — Москва : Интернет-университет информационных технологий, 2006.