Нерівність Єнсена

Нерівність Єнсена — зв'язує визначений інтеграл опуклої функції та значення цієї функції від інтеграла. Вона була доведена данським математиком Йоганом Єнсеном у 1906 році.[1]

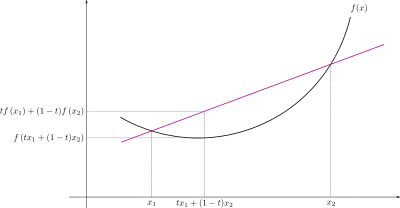
Нерівність Єнсена узагальнює твердження, що січна лінія опуклої функції лежить над її графіком.

Враховуючи свою загальність, нерівність проявляється у багатьох формах залежно від контексту, деякі з яких представлені нижче. У найпростішому випадку нерівність стверджує, що значення опуклого перетворення є меншим або дорівнює значенню отриманого після опуклого перетворення; це простий наслідок того, що обернене твердження вірне щодо перетворень увігнутих функцій.

Нерівність Єнсена узагальнює твердження, що січна опуклої функції лежить над графіком функції (нерівність Єнсена для двох точок): січна лінія утворюється ваговими середніми значеннями опуклої функції (для $t\in [0,1]$ ),

tf(x_{1})+(1-t)f(x_{2}),

у той час як графік функції є опуклою функцією зважених середніх значень

f(tx_{1}+(1-t)x_{2}).

Отже, нерівність Єнсена має вигляд

f(tx_{1}+(1-t)x_{2})\leq tf(x_{1})+(1-t)f(x_{2}).

У контексті теорії ймовірності нерівність як правило подається у наступному вигляді: якщо $X$ — випадкова величина, а $\varphi$ — опукла функція, то

\varphi ({\rm {E}}[X])\leq {\rm {E}}[\varphi (X)].

Різниця між двома частинами нерівності,

{\rm {E}}\left[\varphi (X)\right]-\varphi \left({\rm {E}}[X]\right)

називається проміжком Єнсена [2].

Формулювання

Класична форма нерівності Єнсена включає декілька чисел і вагових коефіцієнтів. Нерівність можна сформулювати у досить загальному вигляді, використовуючи або мову теорії міри, або (що еквівалентно) теорії ймовірності. У термінах теорії ймовірності нерівність можна узагальнити далі.

Дискретний випадок

Для дійсної опуклої функції φ, та чисел $x_{1},x_{2},\dots ,x_{n}$ з її області визначення та додатних чисел a_i, справджується:

\varphi \left({\frac {\sum a_{i}x_{i}}{\sum a_{i}}}\right)\leq {\frac {\sum a_{i}\varphi (x_{i})}{\sum a_{i}}};

нерівність міняє знак, коли φ — угнута функція:

\varphi \left({\frac {\sum a_{i}x_{i}}{\sum a_{i}}}\right)\geq {\frac {\sum a_{i}\varphi (x_{i})}{\sum a_{i}}}.

Рівність виконується тоді і тільки тоді, коли $x_{1}=x_{2}=\dots =x_{n}$ або $\varphi$ є лінійною на її області визначення, що містить $x_{1},x_{2},\dots ,x_{n}$ . Частковим випадком є

\varphi \left({\frac {\sum x_{i}}{n}}\right)\leq {\frac {\sum \varphi (x_{i})}{n}}.

Позначивши $\lambda _{i}={\frac {a_{i}}{\sum _{i=1}^{n}a_{i}}}$ отримаємо еквівалентне формулювання:

f\left(\sum _{i=1}^{n}\lambda _{i}x_{i}\right)\leqslant \sum _{i=1}^{n}\lambda _{i}f(x_{i}),

де

\lambda _{1}+\lambda _{2}+\dots +\lambda _{n}=1.

За допомогою нерівності Єнсена в даному вигляді можна довести:

Інтегральне та ймовірнісне формулювання

Нехай $(\Omega ,A,\mu )$ — ймовірнісний простір, тобто $\mu (\Omega )=1$ . Якщо $g$ — дійснозначна функція, яка є $\mu$ — інтегровною, $\varphi$ — опукла функція на дійсній прямій, тоді [3]

\varphi \left(\int _{\Omega }g\,{\rm {d}}\mu \right)\leq \int _{\Omega }\varphi \circ g\,{\rm {d}}\mu .

У аналізі функцій однієї змінної може знадобитися оцінка для

\varphi \left(\int _{a}^{b}f(x)\,{\rm {d}}x\right),

де $a,b\in {\mathbb {R} }$ та $f\colon [a,b]\to {\mathbb {R} }$ — невід'ємна функція, яка інтегровна за Лебегом. У цьому випадку міра Лебега відрізка $[a,b]$ не обов'язково має дорівнювати одиниці. Однак, за допомогою інтегрування з використанням заміни змінних, інтервал може бути відмасштабований так, що міра дорівнюватиме одиниці. Тоді можна застосувати нерівність Єнсена і отримаємо[4]

\varphi \left({\frac {1}{b-a}}\int _{a}^{b}f(x)\,{\rm {d}}x\right)\leq {\frac {1}{b-a}}\int _{a}^{b}\varphi (f(x))\,{\rm {d}}x.

Аналогічний результат можна сформулювати у термінах теорії ймовірності за допомогою простої зміни позначень. Нехай $(\Omega ,{\mathfrak {F}},P)$ — ймовірністний простір, $X$ — інтегровна дійснозначна випадкова величина, а $\varphi$ — опукла функція. Тоді[5]

\varphi ({\rm {E}}[X])\leq {\rm {E}}[\varphi (X)].

У цьому ймовірнісному формулюванні міра $\mu$ визначається як ймовірність $P$ , інтеграл відносно $\mu$ як математичне сподівання $E$ , а функція $g$ як випадкова величина $X$ .

Зауважимо, що рівність буде мати місце тоді і лише тоді, коли $\varphi$ є лінійною функцією на деякій множині $A$ такій, що $P(X\in A)=1$ (це випливає з наведеного нижче інтегрального доведення).

Загальна нерівність в ймовірнісному формулюванні

Більш загально, нехай $T$ — дійсний топологічний векторний простір, $X$ — $T$ -значна інтегровна випадкова величина. У цих загальних умовах інтегровний означає, що в просторі $T$ існує елемент $E[X]$ , такий, що для будь-якого елемента $z$ із спряженого простору до простору $T$ : $\operatorname {E} |\langle z,X\rangle |<\infty /$ та $\langle z,\operatorname {E} [X]\rangle =\operatorname {E} [\langle z,X\rangle ]$ . Тоді для будь-якої вимірної опуклої функції $\varphi$ та під- $\sigma$ -алгебри ${\mathfrak {G}}$ у $\sigma$ -алгебрі ${\mathfrak {F}}$ :

\varphi \left(\operatorname {E} \left[X\mid {\mathfrak {G}}\right]\right)\leq \operatorname {E} \left[\varphi (X)\mid {\mathfrak {G}}\right].

Тут $\operatorname {E} [\cdot \mid {\mathfrak {G}}]$ є умовним математичним сподіванням відносно $\sigma$ -алгебри ${\mathfrak {G}}$ . Це загальне твердження зводиться до попередніх, якщо топологічний векторний простір $T$ є дійсною віссю, а ${\mathfrak {G}}$ є тривіальною $\sigma$ -алгеброю $\{{\varnothing ,\Omega }\}$ (де $\varnothing$ — порожня множина}, а $\Omega$ — простір елементарних подій)[6].

Уточнена та узагальнена форма

Нехай $X$ — одновимірна випадкова величина із математичним сподіванням $\mu$ та дисперсією $\sigma ^{2}\geq 0$ . Нехай $\varphi (x)$ — двічі диференційована функція, визначимо функцію

h(x)\triangleq {\frac {\varphi (x)-\varphi \left(\mu \right)}{(x-\mu )^{2}}}-{\frac {\varphi '(\mu )}{x-\mu }}.

Тоді[7]

{\begin{aligned}\sigma ^{2}\inf {\frac {\varphi ''(x)}{2}}&\leq \sigma ^{2}\inf h(x)\leq E[\varphi (X)]-\varphi ({\rm {E}}[X])\leq \\&\leq \sigma ^{2}\sup h(x)\leq \sigma ^{2}\sup {\frac {\varphi ''(x)}{2}}.\end{aligned}}

Зокрема, якщо $\varphi (x)$ — опукла функція, то $\varphi ''(x)\geq 0$ і стандартний вигляд нерівності Єнсена безпосередньо випливає, якщо додатково вважати функцію $\varphi (x)$ двічі диференційованою.

Доведення

Графічне доведення нерівності Єнсена для ймовірнісного випадку. Пунктирна крива вздовж осі

X

є гіпотетичним розподілом

X

, тоді як пунктирна крива вздовж осі

Y

є відповідним розподілом значень

Y

. Зауважимо, що опукле відображення

Y(X)

дедалі більше ``розтягує розподіл для збільшення значень $X$ .

Доведення нерівності Єнсена для

n

змінних без слів. Без втрати загальності вважаємо, що сума додатних вагових коефіцієнтів дорівнює 1. Звідси випливає, що вагома точка знаходиться в опуклій оболонці вихідних точок, яка лежить над самою функцією за означенням опуклості. Звідси випливає відповідне твердження.[8]

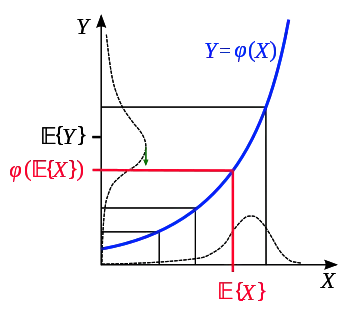
Нерівність Єнсена можна довести декількома способами, і нижче буде запропоновано три різні доведення, що відповідають вищезазначеним твердженням. Однак перед тим як приступати до цих математичних доведень варто проаналізувати інтуїтивно зрозумілий графічний аргумент на основі ймовірнісного випадку, де $X$ є дійсним числом (див. рисунок). Припускаючи гіпотетичний розподіл значень $X$ , можна одразу визначити положення математичного сподівання ${\rm {E}}[X]$ та його образу $\varphi ({\rm {E}}[X])$ на графіку. Враховуючи, що для опуклих відображень $Y=\varphi (X)$ відповідний розподіл значень $Y$ є зростаючим і розтягується при зростаючих значеннях $X$ , легко зрозуміти, що розподіл $Y$ є ширшим в інтервалі, що відповідає $X>X_{0}$ і вужчим при $X<X_{0}$ для будь-якого $X_{0}$ . Зокрема, це також справедливо для $X_{0}={\rm {E}}[X]$ .

Отже, на цьому рисунку математичне сподівання для $Y$ завжди зміщуватиметься вгору по відношенню до положення $\varphi ({\rm {E}}[X])$ . А налогічне міркування справедливе, якщо розподіл $X$ охоплює спадну частину опуклої функції, або одночасно спадну і зростаючу його частини. Це доводить нерівність, тобто

\varphi ({\rm {E}}[X])\leq {\rm {E}}[\varphi (X)]={\rm {E}}[Y],

яка перетворюється у рівність, якщо $\varphi ({X})$ не є строго опуклою функцією, наприклад, якщо вона є прямою, або, якщо $X$ має вироджений розподіл (тобто є константою).

Наведені нижче доведення формалізують це інтуїтивне поняття.

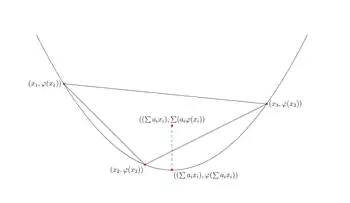
Доведення 1 (дискретна форма)

Якщо $\lambda _{1}$ і $\lambda _{2}$ — два довільні невід'ємні дійсні числа такі, що $\lambda _{1}+\lambda _{2}=1$ , то з опуклості $\varphi$ випливає

\forall x_{1},x_{2}\colon \quad \varphi \left(\lambda _{1}x_{1}+\lambda _{2}x_{2}\right)\leq \lambda _{1}\varphi (x_{1})+\lambda _{2}\varphi (x_{2}).

Цю нерівність можна легко узагальнити: якщо $\lambda _{1},\dots ,\lambda _{n}$ — невід'ємні дійсні числа такі, що $\lambda _{1}+\dots +\lambda _{n}=1$ , тоді

\varphi (\lambda _{1}x_{1}+\lambda _{2}x_{2}+\cdots +\lambda _{n}x_{n})\leq \lambda _{1}\varphi (x_{1})+\lambda _{2}\varphi (x_{2})+\cdots +\lambda _{n}\varphi (x_{n})

для будь-яких $x_{1},\dots ,x_{n}$ . Цю скінченну форму нерівності Єнсена можна довести за допомогою методу математичної індукції: за припущення опуклості твердження справедливе для $n=2$ . Припустимо, що воно справедливе і для деякого $n$ , потрібно довести нерівність для $n+1$ . Щонайменше одне з $\lambda _{i}$ є додатним і строго меншим 1, нехай $\lambda _{1}$ ; тоді з означення опуклості:

{\begin{aligned}\varphi \left(\sum _{i=1}^{n+1}\lambda _{i}x_{i}\right)&=\varphi \left(\lambda _{1}x_{1}+(1-\lambda _{1})\sum _{i=2}^{n+1}{\frac {\lambda _{i}}{1-\lambda _{1}}}x_{i}\right)\\&\leq \lambda _{1}\varphi (x_{1})+(1-\lambda _{1})\varphi \left(\sum _{i=2}^{n+1}{\frac {\lambda _{i}}{1-\lambda _{1}}}x_{i}\right).\end{aligned}}

Оскільки

\sum _{i=2}^{n+1}{\frac {\lambda _{i}}{1-\lambda _{1}}}=1,

то можна застосувати індукційні гіпотези до останнього члена в попередній формулі для того, щоб отримати результат, а саме кінцеву форму нерівності Єнсена.

Для того, щоб отримати загальну нерівність з цієї кінцевої форми, необхідно використовувати аргумент щільності. Скінченну форму можна переписати як

\varphi \left(\int x\,{\rm {d}}\mu _{n}(x)\right)\leq \int \varphi (x)\,{\rm {d}}\mu _{n}(x),

де $\mu _{n}$ — міра, що задається довільною опуклою комбінацією дельта-функцій Дірака:

\mu _{n}=\sum _{i=1}^{n}\lambda _{i}\delta _{x_{i}}.

Оскільки опуклі функції є неперервними, й опуклі комбінації дельта-функцій Дірака є слабко щільними в множині ймовірнісних мір (що можна легко перевірити), то загальне твердження отримується легко за допомогою граничного переходу.

Доведення 2 (інтегральне формулювання)

Нехай $g$ — дійснозначна $\mu$ -інтегровна функція у ймовірностному просторі $\Omega$ , а $\varphi$ — опукла дійснозначна функція. Оскільки $\varphi$ опукла, то для кожного дійсного значення $x$ маємо непусту множину субдиференціалів, які можна розглядати як лінії, що дотикаються до графіка функції $\varphi$ в точці $x$ , але які знаходяться над графіком функції $\varphi$ або нижче нього у всіх точках (опорні лінії графіка).

Тепер, якщо визначимо

x_{0}:=\int _{\Omega }g\,{\rm {d}}\mu ,

то внаслідок існування субдиференціалів для опуклих функцій можемо вибрати $a$ та $b$ такі, що

ax+b\leq \varphi (x)

для всіх дійсних $x$ і $ax_{0}+b=\varphi (x_{0}).$ Але тоді маємо, що $\varphi \circ g(x)\geq ag(x)+b$ для всіх $x$ . Оскільки маємо ймовірнісну міру, то інтеграл є монотонним з $\mu (\Omega )=1$ , так що

{\begin{aligned}\int _{\Omega }\varphi \circ g\,{\rm {d}}\mu &\geq \int _{\Omega }(ag+b)\,{\rm {d}}\mu =\\&=a\int _{\Omega }g\,{\rm {d}}\mu +b\int _{\Omega }{\rm {d}}\mu =\\&=ax_{0}+b=\varphi (x_{0})=\varphi \left(\int _{\Omega }g\,{\rm {d}}\mu \right),\end{aligned}}

що й треба було довести.

Зауваження

Якщо функція $f(x)$ угнута (опукла догори), то знак в нерівності змінюється на протилежний.

Примітки

Jensen, J. L. W. V. (1906). Sur les fonctions convexes et les inegalites entre les valeurs moyennes. Acta Mathematica 30 (1): 175–193. doi:10.1007/BF02418571.
Gao, Xiang; Sitharam, Meera; Roitberg, Adrian (2019). Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions. The Australian Journal of Mathematical Analysis and Applications 16 (2). arXiv:1712.05267.
p. 25 of Rick Durrett (2019). Probability: Theory and Examples (вид. 5th). Cambridge University Press. ISBN 978-1108473682.
Niculescu, Constantin P. "Integral inequalities", P. 12.
p. 29 of Rick Durrett (2019). Probability: Theory and Examples (вид. 5th). Cambridge University Press. ISBN 978-1108473682.
Attention: In this generality additional assumptions on the convex function and/ or the topological vector space are needed, see Example (1.3) on p. 53 in Perlman, Michael D. (1974). Jensen's Inequality for a Convex Vector-Valued Function on an Infinite-Dimensional Space. Journal of Multivariate Analysis 4 (1): 52–65. doi:10.1016/0047-259X(74)90005-0.
Liao, J.; Berg, A (2018). Sharpening Jensen's Inequality. American Statistician. arXiv:1707.08644. doi:10.1080/00031305.2017.1419145.
Bradley, CJ (2006). Introduction to Inequalities. Leeds, United Kingdom: United Kingdom Mathematics Trust. с. 97. ISBN 978-1-906001-11-7.

Див. також

Джерела

Зорич В. А. Математический анализ. — 10-е. — М : МЦНМО, 2019. — Т. 1. — 564 с. — ISBN 978-5-4439-4029-8.(рос.)
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1962. — Т. 1. — 607 с.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Jensen, J. L. W. V. (1906). Sur les fonctions convexes et les inegalites entre les valeurs moyennes. Acta Mathematica 30 (1): 175–193. doi:10.1007/BF02418571.

[Gao_et_al.-2] Gao, Xiang; Sitharam, Meera; Roitberg, Adrian (2019). Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions. The Australian Journal of Mathematical Analysis and Applications 16 (2). arXiv:1712.05267.

[3] . 25 of Rick Durrett (2019). Probability: Theory and Examples (вид. 5th). Cambridge University Press. ISBN 978-1108473682.

[4] Niculescu, Constantin P. "Integral inequalities", P. 12.

[5] . 29 of Rick Durrett (2019). Probability: Theory and Examples (вид. 5th). Cambridge University Press. ISBN 978-1108473682.

[6] Attention: In this generality additional assumptions on the convex function and/ or the topological vector space are needed, see Example (1.3) on p. 53 in Perlman, Michael D. (1974). Jensen's Inequality for a Convex Vector-Valued Function on an Infinite-Dimensional Space. Journal of Multivariate Analysis 4 (1): 52–65. doi:10.1016/0047-259X(74)90005-0.

[Liao_&_Berg-7] Liao, J.; Berg, A (2018). Sharpening Jensen's Inequality. American Statistician. arXiv:1707.08644. doi:10.1080/00031305.2017.1419145.

[8] Bradley, CJ (2006). Introduction to Inequalities. Leeds, United Kingdom: United Kingdom Mathematics Trust. с. 97. ISBN 978-1-906001-11-7.