Рівняння мілкої води
Рівняння мілкої води (відоме також, як рівняння Сен-Венана в лінійній формі) — система гіперболічних диференціальних рівнянь в часткових похідних, яка описує потоки під поверхнею рідини.
| Механіка суцільних середовищ |
|---|
 |
|
Тверде тіло:
Напруження • Деформація • Теорія малих деформацій • Теорія великих деформацій • Теорія пружності • Механіка контактної взаємодії • Опір матеріалів • Теорія пластичності • Механіка руйнування |
|
Флюїд: Тиск • Гідростатика (закон Архімеда; закон Паскаля) • Гідродинаміка (закон Бернуллі) • В'язкість (ньютонівська рідина; неньютонівська рідина) Рідина: Поверхневий натяг • Капілярний ефект |
|
В'язкоеластичність • Розумні рідини (Магнетореологічна рідина, Електрореологічна рідина, Феромагнітна рідина) • Реометрія |
|
Основні рівняння |

Рівняння отримуються[1] шляхом інтегрування по глибині Рівняння Нав'є — Стокса за умови, що горизонтальний масштаб більший, аніж вертикальний. При цій умові зі закону нерозривності випливає, що вертикальні швидкості в рідині є малими, вертикальні градієнти тиску близькі до нуля, а горизонтальні градієнти спричиняються нерівністю поверхні рідини однакові по всій глибині. При інтегруванні по вертикалі вертикальні швидкості виводяться з рівнянь.
Хоча вертикальні швидкості відсутні у рівняннях мілкої води, вони не обов'язково дорівнюють нулю. Це важливо, оскільки вертикальна швидкість не може бути рівною нулю, наприклад, при вимірюванні глибини акваторії. Нульовій вертикальній швидкості відповідає тільки випадок плоского дна. Коли отримано горизонтальні швидкості, вертикальні швидкості виводяться з рівняння неперервності.
Ситуації, коли глибина акваторії набагато менша, аніж горизонтальні розміри, достатньо поширена, тому рівняння мілкої води мають широке застосування. Вони використовуютьсяз уразуваннням коріолісових сил при моделювання атмосфери і океану, як спрощення примітивних рівнянь, які описують потоки в атмосфері.
Рівняння мілкої води враховують тільки один вертикальний рівень, тому вони не можуть описувати фактори, які міняються з глибиною. Тим не менше, коли динаміка потоків у вертикальному напрямку відносно проста, вертикальні зміни можуть бути відокремлені від горизонтальних і стан такої системи можна описати кількома системами рівнянь для мілкої води.
Рівняння
Консервативна форма
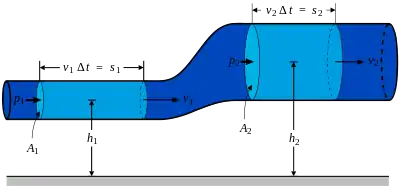
Рівняння мілкої води виводяться з рівнянь збереження маси та імпульсу (рівняння Нав'є-Стокса), які справедливі для загального випадку, в тому числі в ситуаціях, коли умови мілкої води не виконуються. Без врахування сил Коріоліса, тертя и в'язкості рівняння мають вигляд:
Некосервативна форма
Рівняння можуть бути записані для швидкостей. Оскільки швидкості не входять у фундаментальні закони збереження, ці рівняння не описують явища типу гідравлічного удару чи гідравлічного стрибка.
де
— швидкість вздовж осі x; — скорость вдоль осі y; — середня висота поверхні рідини; — відхилення тиску в горизонтальній площині від середнього значення; — прискорення вільного падіння; — Параметр Коріоліса, що дорівнює на Землі — кутова швидкість обертання Землі навколо осі ( радіан/година); — географічна широта; — коефіцієнт в'язкого опору.
Застосування в моделюванні
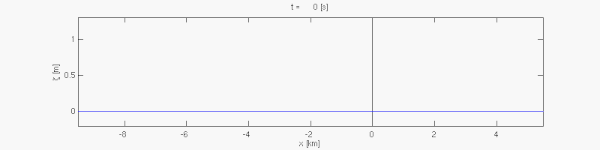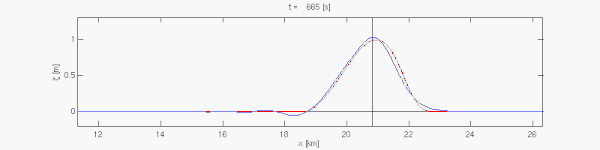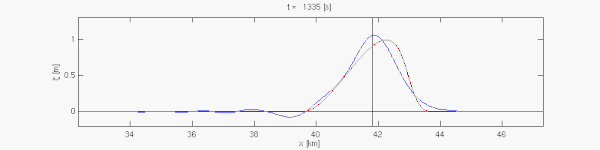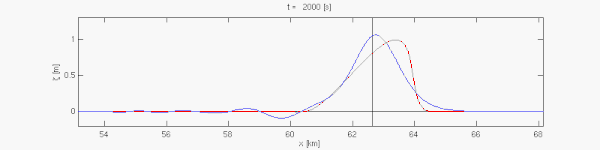
Рівняння мілкої води можна застосовувати для моделювання Россбі та Кельвіна в атмосфері, ріках, озерах, океанах, а також мілкіших водоймах, таких як басейн. Для того, щоб застосування рівнянь мілкої води було коректним, горизонтальні розміри акваторії мають бути значно більшими, ніж глибина. Рівняння мілкої води придатні також для моделювання припливів. Припливні рухи, які мають горизонтальні масштаби в сотні кілометрів, можуть ввжатись явищами мілкої води, навтіь якщо відбуваються над багатокілометровими океанськими глибинами
Примітки
- David A. Randall (6 липня 2006). The Shallow Water Equations (англ.). Архів оригіналу за 6 вересня 2012. Процитовано 17 грудня 2011.
Література
- Савула Я. Метод скінченних елементів (окремі[які?] сторінки посібника 1993 р.) http://old.ami.lnu.edu.ua/books/AMI/savula.pdf
- Шинкаренко Г. Чисельні методи математичної фізики (окремі[які?] сторінки чорновика посібника)http://old.ami.lnu.edu.ua/books/AMI/nmmf.pdf
