Тензорна алгебра

Нехай V — векторний простір над полем k. Для будь-якого натурального числа k визначимо k-ий тензорний степінь V як тензорний добуток V на себе k раз :

${\displaystyle T^{k}V=V^{\otimes k}=V\otimes V\otimes \cdots \otimes V}$

Таким чином, T^k V складається з усіх тензорів над V рангу k. Будемо вважати, що T⁰ V — основне поле k (одновимірний векторний простір над собою).

Визначимо T(V) як пряму суму T^k V для всіх k = 0,1,2, ...

${\displaystyle T(V)=\bigoplus _{k=0}^{\infty }T^{k}V=K\oplus V\oplus (V\otimes V)\oplus (V\otimes V\otimes V)\oplus \cdots }$

Добуток в T(V) визначається заданим тензорним добутком канонічним ізоморфізмом:

${\displaystyle T^{k}V\otimes T^{\ell }V\to T^{k+\ell }V}$

який потім продовжується по лінійності на всю T(V). Таке множення перетворює тензорну алгебру T(V) в градуйовану алгебру.

Тензорна алгебра T(V) — вільна алгебра векторного простору V. Як і для будь-якої іншої вільної конструкції, функтор Т є лівим спряженим функтором забуваючого функтора (який в даному випадку відправляє К-алгебру в її векторний простір). Тензорна алгебра задовольняє універсальну властивість, яка формалізує твердження, що це найбільш загальна алгебра, що містить простір V:

Будь-яке лінійне відображення ${\displaystyle f:V\to A}$ простору V над полем К в алгебру A над k може бути єдиним чином продовжено до гомоморфізма алгебр ${\displaystyle {\bar {f}}:T(V)\to A}$. Це твердження виражається комутативною діаграмою:

Universal property of the tensor algebra

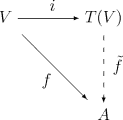
де i — канонічне вкладення V в T(V). Тензорну алгебру можна визначити як єдину (з точністю до ізоморфізму) алгебру, що володіє такою властивістю, хоча необхідно ще явно показати, що така алгебра існує.

Наведена вище універсальна властивість показує, що тензорна алгебра функторіальна, тобто T — функтор з категорії K-Vect векторних просторів над K в категорію k-Alg K-алгебр. Функторіальность Т означає, що будь-яке лінійне відображення з V в W може бути єдиним чином продовжено до гомоморфізму з алгебри T(V) у T(W).

Якщо розмірність V є скінченною і дорівнює n, то тензорну алгебру можна розглядати як алгебру многочленів над k з n некомутативними змінними. Базисним векторам V відповідають некомутативними змінні, причому їх множення буде асоціативним, дистрибутивним і k — лінійним.

Зауважимо, що алгебра многочленів над V - це не ${\displaystyle T(V)}$, а ${\displaystyle T(V^{*})}$: однорідна лінійна функція на V є елементом спряженого простору ${\displaystyle V^{*}}$.

Зважаючи на загальність тензорної алгебри багато інших важливих алгебр на просторі V можна отримати, накладаючи певні обмеження на твірні елементи тензорної алгебри, тобто як факторалгебри від T(V). Наприклад, так можна побудувати зовнішню алгебру, симетричну алгебру і алгебру Кліффорда.

Конструкція тензорної алгебри над лінійним простором природно узагальнюється до тензорною алгебри над модулем M над комутативним кільцем. Якщо R - некомутативне кільце, можна побудувати тензорний добуток для будь-яких R-бімодулів над M. Для звичайних R-модулів є неможливою побудова кратного тензорного добутку.

• Алгебра Кліфорда
• Зовнішня алгебра
• Симетрична алгебра

• Винберг Э. Б. Курс алгебри. — 4-е изд. — Москва : МЦНМО, 2011. — 592 с. — ISBN 978-5-94057-685-3.(рос.)

• Ленг С. Алгебра. — Москва : Мир, 1968. — 564 с. — ISBN 5458320840.(рос.)
• Бурбаки Н. Алгебра. Часть 1. Алгебраические структуры. Линейная и полилинейная алгебра. — Москва : ГИФМЛ, 1962. — С. 516.(рос.)