Кодування кінематики руху моторною корою
Кодування кінематики руху моторною корою характеризує відношення нейронного кодування між активністю одиничних та популяції нейронів в моторній корі та кінематичними параметрами руху (напр., напрямок, швидкість, положення, траєкторія) верхніх кінцівок, які ця активність репрезентує.
Однією з головних і найдискусійніших проблем нейрофізіології моторного керування рухами верхніх кінцівок є питання, якою є природа вихідних команд моторної кори (і зокрема, первинної моторної кори), яка відіграє ключову роль у плануванні, підготовці та виконанні довільних рухів. Подібно до нейрофізіології сенсорних систем, більшість досліджень нейронної активності в моторній корі ґрунтуються на припущенні, що нейрони цієї області кори головного мозку кодують конкретні моторні параметри, пов'язані з рухом руки в просторі. Однак, нейронауковці розходяться щодо того, які саме параметри кодують нейрони в моторній корі.
Щодо первинної моторної кори (М1), яка відіграє ключову роль у керуванні довільними рухами, проблема нейронного кодування полягає в тому, чи кодують нейрони М1 моторні параметри вищого порядку, пов'язані з цілями та зовнішніми, просторовими координатами (кінематику руху), або ж параметри нижчого порядку, пов'язані з моторною периферією та внутрішніми змінними (кінетикою)?
Кінетика (динаміка) руху стосується сил руху, що генеруються склетеними м'язами; крутних моментів, породжуваних силами на суглобах; рівнодійної сили, генерованої цілою кінцівкою. Кінематика ж руху відноситься до зовнішніх, просторових змінних руху: положення в просторі, швидкість, прискорення, напрямок і траєкторія руху.
Нейронауковці, які займають «кінетичну позицію», вважають, що М1 визначає точну активацію м'язів довкола суглобів таким чином, щоб генерувати необхідні крутні моменти, які перемістять руку до вибраної поведінкової цілі. Нейронауковці ж, які займають кінематичну позицію, вважають, що М1 кодує лише просторову траєкторію руху руки. Ця група дослідників визнає, що м'язова активність та крутні моменти повинні визначатись на деякому рівні моторної системи, без чого рух багато-сегментної кінцівки був би неможливим, але вони відводять роль у кодуванні цих параметрів нейронам спинного мозку.
Кодування моторних параметрів руху
Для вивчення того, що кодує нейронна активність в М1, одним з перших і найпоширеніших підходів серед нейрофізіологів була реєстрація активності одиничних нейронів притомних мавп під час виконання ними різноманітних сенсорно-моторних завдань, як то рух зап'ястка, просторові досягання від однієї точки до іншої чи тримання кисті руки на просторових цілях за різних механічних умов. Незважаючи на складність нейронної активності в обробці інформації, подібні дослідження автоматично припускали, що характерна форма розрядів нейронів може бути пояснення на основі кореляції з певними очевидними рисами конкретної сенсорно-моторної поведінки.
Американський нейрофізіолог Едвард Евартс першим використав хронічні позаклітинні мікроелектродні реєстрації множини одиничних нейронів для вивчення природи нейронного кодування в М1 притомних мавп.[1][2] На основі дослідження нейронної активності в М1 (зокрема, пірамідного шляху) Евартс припустив, що нейрони в М1 кодують величину сили (кінетику), необхідну для генерування руху, а не сам рух кінцівки (кінематику).
З робіт Евартса бере початок традиція у вивченні моторної системи, згідно з якою, подібно до сенсорних областей кори, нейронауковці намагались знайти нейронний код моторної кори.
Кодування напрямку руху
До початку 1970-х рр. нейрофізіологічні дослідження моторної кори фокусувались головним чином на взаємозв'язку між активністю одиничних нейронів в М1 та рухом одиничних суглобів. Американський нейрофізіолог Дональд Хамфрі (Donald R. Humphrey) разом з колегами вперше показав, що відповідним чином зважена сума активності невеликої групи нейронів в моторній корі краще корелює з параметрами руху зап'ястя в ізотонічному завданні, аніж активність одиничних нейронів.[3] Хамфрі виявив, що якщо оптимально підібрати для кожного параметру руху зап'ястя зважені параметри одиничних нейронів, то зважені суми частот розрядів нейронів будуть збігатися з траєкторіями сили м'язів та переміщення зап'ястя.[4] А додаючи ще більше нейронів до популяції можна було значно покращити відповідність між зваженими розрядами нейронів та механічними параметрами, оскільки кожен ненадлишковий додатковий нейрон зменшував залишкову різницю. Це було першим відкриттям механізму популяційного кодування параметрів руху моторною корою.
Направлена налаштованість одиничних нейронів
Хоча завдання з одним суглобом є популярними та корисними для вивчення багатьох питань, пов'язаних з нейронним кодуванням рухів, з їхньою допомогою неможливо розв'язати низку проблем моторного керування, які постають, коли рух включає другий суглоб. По-перше, між конечним ефектором (кистю руки) та рухами суглобів нема простого лінійного відображення: рух кисті до конкретного місця в просторі може бути виконаний з використанням багатьох різних просторових траєкторій через зміну координації рухів двох суглобів. По-друге, відношення між рухом суглобу та крутним моментом суглобу істотно різниться в одно-суглобовій та багато-суглобовій системах. Тоді як крутний момент та рух лінійно пов'язані в одно-суглобовій системі, то внаслідок міжсегментної динаміки в багато-суглобовій системі не існує простого відображення між рухом та крутним моментом: крутний момент в одному суглобі може привести до руху в інших суглобах, а багато-суглобовий крутний момент викликати рух одиничного суглобу.[5][6] Тому, коли рух включає більше, аніж один суглоб, то моторна система повинна ретельно координувати моторні патерни одного суглобу з патернами іншого, щоб зробити рух в просторі настільки плавним, наскільки можливо.[7]
Перше дослідження нейронної активності в моторній корі під час завдання на досягання всією рукою було здійснене на початку 1980-х відомим американським нейрофізіологом Апостолосом Георгопулосом (англ. Apostolos P. Georgopoulos), який з колегами в серії новаторських досліджень виявив стійкий зв'язок між активністю популяції нейронів та напрямком природних рухів.
Результати ранніх нейрофізіологічних досліджень припускали, що моторна кора керує багато-сегментними рухами досягання через поєднання рухів одиничних суглобів. Тоді як Георгопулос, — на основі поведінкових даних, що рухи досягання рукою включають добре координовані та тісно пов'язані рухи суглобів плеча та ліктя, які переміщають руху до бажаного місця в просторі,[8] — припустив, що ЦНС керує рухами верхніх кінцівок, як пов'язаною, єдиною системою, а не як сукупністю окремих одиниць.
Отримані Георгопулосом та колегами дані дійсно свідчили, що моторна кора визначає та керує рухами досягання, як організованими, багато-сегментними рухами, підтверджуючи давнє припущення про те, що моторні команди визначають цілісні рухи руки, призначені для певних поведінкових цілей, а не деталі м'язових скорочень протягом виконання цих рухів.[9]
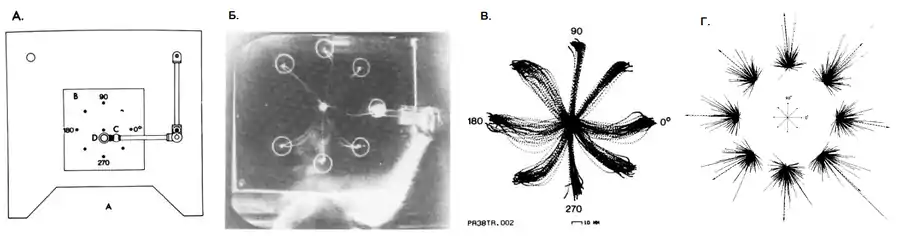
У першій статті, яка змінила усталений погляд на керування рухами моторною корою, Георгопулос та ін. досліджували нейронну активність мавпи, яка рухала маніпуляндум до візуальних цілей на плоскій поверхні (операційний простір).[10] На відміну від рухів відносно одного суглобу (напр., згинання/розгинання в лікті), рухи досягання включають добре скоординовані та тісно поєднані рухи суглобів плеча та ліктя і зазвичай спрямовані в бік візуальних цілей. Рухи досягання переміщують кінцівку від початкової точки до бажаного місця в просторі і складаються з двох просторових компонентів — напрямку та амплітуди.
Складність у вивченні відношення нейронної активності до напрямку руху полягає в тому, що напрямок є сферичною, а не лінійною змінною. Відтак, існують два способи репрезентувати напрямок: 1) для відображення конкретного напрямку призначити конкретний нейрон і 2) репрезентувати напрямок через ансамбль нейронів. В першому випадку, рухи досягання в бажаному напрямку будуть здійснюватись через залучення нейронів, які мають відповідну направленість, тоді як в другому випадку, увесь ансамбль нейронів буде залучений в такий спосіб, який дозволить однозначно репрезентувати напрямок в активності даного ансамблю. Дослідження Георгопулоса та колег показали що саме другий спосіб притаманний нейронам моторної кори.
Із виділених дослідниками ~600 нейронів в моторно-кортикальній області руки, 323 проявляли активність протягом поставленого завдання: їхня інтенсивність розрядів, знак зміни (збільшення/зменшення розряду) та час настання цих змін систематично змінювались з напрямком руху. Більшість із цих нейронів змінювали частоту розрядів залежно від руху руки в більш ніж одному, частіше всіх, напрямках. Тобто, подібно до вибіркової налаштованості одиничних нейронів в зоровій корі по відношенню до орієнтації, положення чи форми стимулу, одиничні нейрони М1 проявляли налаштованість до певного напрямку руху (т. зв. «направлена налаштованість», англ. directionally tuned), оскільки частота їхніх розрядів була найвищою для конкретного напрямку (т. зв. «переважний напрямок» нейрону, англ. preferred direction) і поступово спадала, коли рука рухалась в напрямках, протилежних переважному напрямку. Подібний зв'язок з напрямком спостерігався у нейронних розрядах ще до перших змін в електроміографії, за 80 мс до настання руху, припускаючи, що зв'язок нейронної активності з напрямком руху руки не був результатом периферійного зворотного сигналу.
241 із 323 нейронів, які мали найвищу частоту розрядів в одному напрямку руху та нижчу в усіх інших напрямках, класифікувались, як направлено налаштовані і їхня активність (криві частотного налаштування; англ. tuning curve) найкраще апроксимувалась синусоїдальною функцією від напрямку руху: частота їхніх розрядів, , синусоїдально змінювалась залежно від кута, , напрямку руху.
(1)
або в термінах нейронного «переважного напрямку», ,
(2)
де — це «переважний напрямок», , основна (середня) частота розрядів, а та — скалярні величини.
Тобто, коли мавпа робила рух руки в певному напрямку, то активізувались нейрони, «направлена перевага» яких збігалася чи була близькою до цього напрямку руху, а нейрони з протилежною чи віддаленою «направленою перевагою», гальмувались. Особливий розподіл збудження та гальмування серед направлено налаштованих нейронів утворював популяційний код для напрямку руху.[10]
Головним відкриттям цього дослідження Георгопулоса та ін. було те, що активність нейрону змінювалась залежно від кількох, а не тільки одного напрямку руху. Тобто, одиничні нейрони не кодували один конкретний напрямок, а як свідчила систематична, синусоїдальна зміна кривих налаштування, — нейрони з кривими, що перекривались, разом генерували траєкторію руки в бажаному напрямку. Тим самим, змінні руху кодувались не одиничним нейроном, як припускали ранні нейрофізіологічні дослідження, а популяцією нейронів. Крім того, робота Георгопулоса та колег продемонструвала, що протягом природної поведінки активність нейронів моторної кори найкраще співвідносилась з напрямком руху в просторі, що свідчило на користь кодування кінематичної змінної руху моторною корою.[10]
Нейронний вектор популяції
Як показали пізніші дослідження, виявлена Георгопулосом та ін. функція направленого налаштування активності одиничного нейрону мала три ключові риси: 1) вона широка, що означало що активність нейрону змінювалась у всьому діапазоні напрямків, як в двовимірному,[10][11] так і в трьох-вимірному[12][13] 2) вона змінювалась впорядковано і добре описувалась косинусною функцією і 3) вона симетрична та унімодальна, тобто, існують напрямки, для яких частота розрядів нейронів буде найвищою («переважний напрямок» нейрону); різні нейрони мали різні переважні напрямки, які охоплювали увесь континуум напрямків.
З цих властивостей функції направленого налаштування випливало, що (за винятком пікової активності) активність нейрона містила двозначну інформацію про напрямок руху, оскільки одна і та ж частота розрядів нейрону могла відповідати двом різним напрямкам. Відтак, даний нейрон активізувався під час рухів в різних напрямках і тому рух в конкретному напрямку включав активацію всієї популяції нейронів. Поставало тоді питання, яким чином напрямок руху може однозначно кодуватись популяцією нейронів, якщо кожен з них має широку направлену налаштованість?

Георгопулос та колеги, вивчаючи активність нейронів моторної кори мавпи під час рухів в тривимірному просторі, запропонували популяційний код, який однозначно визначав напрямок руху.[12][14]
Відношення між напрямком досягального руху, , та частотою розряду нейрону, , виражалось функцією широкого налаштування, , пік якої означував «переважний напрямок» нейрону, , тобто, напрямок руху, по відношенню до якого частота розрядів нейрону буде найвищою. Переважні напрямки направлено-налаштованих нейронів охоплювали весь тривимірний континуум напрямків відносно початку руху. Зміни в активності нейрону були пов'язані з напрямком, а не з ціллю руху руки. Головною змінною, від якої залежала ця активність нейрону, був кут, , між напрямком руху досягання руки та переважним напрямком нейрону . Пік активності нейрону (найвища частота розрядів) протягом рухів до інших напрямків найкраще апроксимувався лінійною функцією косинуса кута між переважним напрямком нейрону та напрямком руху. Тоді направлену налаштованість нейрона можна виразити як
(3)
де — це передбачений розряд i-го нейрону коли рух здійснюється в напрямку , — переважний напрямок нейрону, і — це константи для цього нейрону, а — кут між переважним напрямком нейрону та напрямком руху руки. З цього випливало, що частота розряду нейрону буде найвищою тоді, коли рухи руки будуть в «переважному напрямку» нейрону (коли та будуть однаковими), найнижчою — коли рухи будуть в протилежному напрямку, і середньою — коли рухи будуть в проміжних напрямках. Це дозволяє, якщо відомий розряд нейрону для переважного напрямку, передбачити розряд для будь-якого іншого напрямку руху.[14]
З рівняння (3) також випливає, що нейрони моторної кори є широко налаштованими, тобто змінюють свою активність коли рука рухається в будь-якому напрямку. Тоді як вузько налаштованих нейронів, які б змінювали свою активність залежно тільки від одного чи двох прилеглих напрямків рухів, Георгопулос та ін. не виявили.
Однак така широка налаштованість кожного нейрону М1 накладала певну проблему на кодування руху: як можна отримати конкретний, точний напрямок руху із подібних широких, косинусних кривих налаштування? Як показав Георгопулос та ін., напрямок руху кодується не індивідуальними нейронами, які реагують на рухи в конкретному напрямку, а направлено налаштованою популяцією нейронів. Тому рух є результатом активності всієї популяції нейронів в М1.
В основі нейронного популяційного кодування напрямку руху лежить оригінальна ідея Георгопулоса: оскільки направлено налаштований нейрон має переважний напрямок, то популяцію таких нейронів може бути задано як ансамбль векторів, кожен з яких вказує в переважному напрямку конкретного нейрону.[14]
Переважні напрямки нейронів залишаються незмінними для різних рухів, тоді як інтенсивність розряду нейрону є функцією напрямку руху (рівн. 3), тому й довжина вектора, , i-го нейрону для руху в напрямку змінюватиметься відповідно, та буде рівною зміні розряду нейрону, , пов'язаному з цим напрямком руху, мінус величина зміщення, :
(4)
Тобто, нейрони, чий переважний напрямок близький до напрямку руху руки, роблять більший внесок, а ті нейрони, чий переважний напрямок віддалений, мають менший внесок до популяційного коду.
Додавши всі вектори напрямків одиничних нейронів, Георгопулос отримав вектори, орієнтовані в напрямку виконуваних рухів. Зважена векторна сума внеску популяції нейронних векторів дозволила сформулювати «вектор популяції».
Формально, вектор популяції виражається, як
де — це нейронний вектор популяції для руху в напрямку ; — кількість нейронів в популяції; це направлена перевага i-го нейрону в популяції; а — це зважена функція, яка відображає величину внеску i-го нейрону в популяційний вектор для руху в напрямку . Тобто, кожному нейрону приписується пара ваг відповідно до його переважного напрямку. Зважена сума — це сума активностей всіх нейронів, зважених відповідно до того ступеня, до якого даний нейрон віддає перевагу певному напрямку руху.
Коли Георгопулос зобразив активність всіх одиничних нейронів протягом кожного руху, як множину векторів, то отриманий розподіл векторів виявив сильне направлене відхилення, яке систематично зміщувалось з напрямком руху.[12]
Тож, інформацію щодо напрямку руху можливо однозначно отримати із популяції нейронів і завдяки ній передбачити напрямок майбутнього руху руки. Саме тому вектор популяції є в основі майже всіх наявних сьогодні нейрокомп'ютерних інтерфейсів.[15][16][17]
Відкриття Георгопулосом та ін. популяційного кодування напрямку руху первинною моторною корою підтверджувало, що саме кінематичні параметри руху репрезентуються нейронною активністю в М1. Оскільки протягом руху досягання багато м'язів активуються одночасно, то пряме відношення між одиничними нейронами М1 та одиничними м'язами повинно характеризуватись складним зв'язком із напрямком руху. Натомість Георгопулос та ін. знайшли просту, широку налаштованість нейронів М1 до напрямку руху. Це було першим відкриттям функціональної ролі моторної кори: багато нейронів моторної кори активізувались у відповідь на напрямок руху і тому кодували кінематичні моторні параметри, незалежно від конкретних м'язів, які вони іннервували. Тоді як функцією спинномозкових нейронів було перетворення кінематичних змінних у відповідні конкретні сигнали активації м'язів.

Застосування вектора популяції
Продуктивність популяційного коду руху була підтверджена Георгопулосом та іншими в серії новаторських досліджень. В одному з досліджень, з допомогою нейронного вектора популяції вдалось передбачити напрямок майбутнього руху протягом часу реакції — період який триває ~300 мс між появою візуальної цілі та ініціювання руху і протягом якого планується рух та розпочинається його виконання.[18]
Окрім того, з допомогою вектора популяції змогли точно перебачити напрямок руху протягом навченого періоду затримки.[19] Мавп навчили затримувати рух на деякий час після появи візуального сигналу і рухати рукою пізніше, у відповідь на сигнал «пішов». Протягом цього періоду затримки, вектор популяції міг достовірно передбачити напрямок руху, який мавпа ініціювала після завершення цього періоду.
У ще складнішому завданні з допомогою вектора популяції вдалось передбачити напрямок руху протягом запам'ятовуваного періоду затримки.[20] В цьому дослідженні ціль руху була показана тільки на 300 мс. Мавпу навчили затримувати рух на такий же період часу, протягом якого цілі не було, а потім рухати руку в напрямку запам'ятованої цілі у відповідь на сигнал «пішов». Протягом цього запам'ятованого періоду затримки вектор популяції вказував у напрямку запам'ятованого руху.
Оскільки вектор популяції може бути обчислювано в часі (напр. кожні 10 чи 20 мс), він дає можливість неперервного зчитування активності нейронів моторної кори, що уможливлює передбачування майбутньої моторної поведінки. Додана популяційна активність нейронів на кожному наступному 20 мс часовому відрізку систематично варіювалась із напрямком руху в 3D просторі, починаючи від 100 мс до настання руху аж до його завершення. Коли були додані начала до кінців 20 мс векторів популяції, то отриманні нейронні траєкторії досить точно узгоджувались з реальними просторовими траєкторіями руки під час досягання до кожної цілі.[22]
Окрім того, точність вектора популяції є відносно стійкою до втрат нейронів і може вдало передбачити напрямок руху навіть всього лишень з 20 направлено налаштованими нейронами.[23]
Найоригінальнішим чином передбачувальна властивість вектора популяції проявилась у вивченні когнітивних процесів, пов'язаних з напрямком руху, зокрема ментальних трансформацій напрямку. Макак резус було навчено виконувати ментальне обертання. Вони дивилися на вісім кнопок, розміщених по колу. Коли одна кнопка спалахувала світлом, мавпа повинна була досягнути та торкнутись кнопки, яка знаходилась на 90° проти годинникової стрілки від освітленої кнопки. Реєстрація нейронної активності мавпи та обчислення змінного за часом вектора популяції виявили, що протягом часу реакції, між освітленням кнопки та настанням руху, вектор популяції нейронів М1 спочатку вказував в напрямку освітленої кнопки, а потім поступово, проти годинникової стрілки обернувся в напрямку руху руки. В інших завданнях цього ж експерименту, мавпа повинна була рухати руху в напрямку стимулу. В цьому випадку, вектор популяції не обертався, а вказував в напрямку стимулу.[24][25]
Пізніші дослідження виявили нейронні кореляти рухів руки в первинній сомато-сенсорній корі,[26] в області 5 тім'яної кори,[27] в дорсальній премоторній корі,[28] в мозочку,[29] дорсальному спинно-мозочковому шляху (шлях Говерса),[30] в м'язових аферентних сигналах[31][32] і навіть в м'язовій активності проксимальної кінцівки.[33] Втім, саме в первинній моторній корі було відкрито стійкі нейронні кореляти зовнішніх просторових направлених та навіть ненаправлених (скалярних) параметрів, таких як: напрямку руху, положення цілі в просторі, відстані руху, швидкості та тангенціального прискорення протягом прямолінійного досягання та фігурних рухів.[34][35][36][37][38][39][40]
З результатів досліджень активності популяції нейронів під час рухів всією рукою у декартовому просторі випливало, що первинна моторна кора містить детальну репрезентацію просторово-часових траєкторій рухів, виражену у формі зовнішньо-просторової кінематики руху, включаючи напрямок, швидкість та прискорення руху. Тому припускалось, що М1 повинна знаходитись на досить ранніх щаблях ієрархії моторного керування, визначаючи загальну форму рухів кінцівки, а не механічні властивості їхньої реалізації.[41] Вважалось, що нейронна активність, що корелює з рухом в просторі, забезпечує спільну мову вищого порядку, яка дозволяє М1 взаємодіяти з іншими областями ЦНС.[42]
Недоліки векторного коду
Кореляція між популяційною функцією та рухом руки в просторі не може бути повним описом нейронної активності в моторній корі, оскільки не дає причинного пояснення мережі синаптичних зв'язків та відношення між вектором популяції та м'язовою активністю і механікою кінцівки.
Критики векторної гіпотези вказували на те, що вона буде корелювати з нейронною активністю та достовірно вказувати напрямок руху, навіть якщо такої кореляції насправді нема.[43] Для даного конкретного руху, за умови достатнього розподілу нейронів, ті нейрони, чий переважний напрямок найкраще збігатиметься з напрямком руху, матимуть найбільший прямий внесок. Нейрони, чиї вектори вказуватимуть в протилежному напрямку, матимуть від'ємний векторний внесок, оскільки середні частоти віднімаються, а тому вони також роблять позитивний внесок у напрямок руху. Внесок нейронів, які матимуть позаосьові векторні компоненти, анулюватиметься із достатньо великою нейронною популяцією. Тому векторна гіпотеза буде узгоджуватись з напрямком руху незалежно від того, чи мають направлено-налаштовані нейрони який-небудь вплив на м'язову активність, чи ні.[44][45]
Хоча нейронні кореляти напрямку руху в М1 забезпечують важливий зв'язок з моторною поведінкою, залишається незрозумілим, яким чином можна поєднати ці команди вищого порядку з активністю нижчого порядку — спинномозковими нейронами та м'язами, які підтримують складні багато-суглобові та координовані рефлекторні моторні реакції.[46][47][48][49][50]
Навіть якщо активність одиничних нейронів та їхніх популяцій корелює з напрямком руху, це ще не свідчить про те, що нейрони М1 кодують виключно напрямок руху. М'язова активність, до прикладу, також змінюється разом з напрямком руху, а тому нейрони в М1 можуть кодувати м'язові параметри, а не сам рух. Результати анатомічних та нейрофізіологічних досліджень, на основі спайк-зумовленого усереднення показали, що одиничні нейрони моторної кори впливають на кілька пулів мотонейронів, а відтак можуть активувати багато м'язів, які часто розподілено вздовж більше ніж одного суглобу.[51][52][53] В такому випадку, нейрони, напр., можуть залучати різні м'язи з різними силами, формуючи множину м'язів з переважним напрямком, а відтак створюючи велику кількість потенційних переважних напрямків, в які може бути спрямовано нейрони М1. Тоді під час руху в багатьох різних напрямках активуватиметься множина м'язів, на які проєктується даний нейрон, тим самим обумовлюючи достатньо широку направлену налаштованість нейрону, яку спостерігав Георгопулос та ін. експериментально. Тож напрямок руху в просторі не є єдиною можливою інтерпретацією вектора популяції, отриманого з активності групи нейронів, чи переважного напрямку одиничних нейронів в М1.[54]
Кілька теоретичних моделей переконливо продемонстрували, що нейронна активність може передбачувати напрямок руху руки, навіть якщо нейрони кодують інші параметри моторної поведінки, напр. активність м'язів чи суглобів. Математичний аналіз Фердинанда Мусси-Івальді переконливо показав, як розв'язок матричного перетворення між напрямком шляху руки та змінними стану м'язів плеча передбачує, що нейрони, які кодують довжину м'язів плеча та частоту зміни довжини м'язів, матимуть такі самі косинусні криві налаштування, як і нейрони моторної кори.[55] Ці ж самі властивості моторних нейронів виникали в моделях штучних нейронних мереж, де косинусні криві налаштування поставали як результат навчання лінійного відображення між просторовими напрямками та обертаннями суглобів, а не бувши закладеними до моделі нейрону.[56][57] Результати Мусси-Івальді також узгоджувалися з моделями моторного керування, в яких такі кінематичні параметри, як рух, були емерджентною властивістю взаємодії між обчислено запрограмованими силами та навантаженнями кінцівки,[58] або ж поставали як результат кодування популяцією нейронів м'язової активності, а не через вектори популяції.[59] Тим самим ці теоретичні та обчислювальні результати, на відміну від вектора популяції, поєднали нейронне кодування руху руки із фактом, що багато прецентральних нейронів кори дійсно мають вплив на м'язову активність.[60]
Також про не цілковиту відповідність векторної моделі з моторною активністю в корі свідчили відкриття того, що кореляція частоти розрядів нейронів в М1 з просторовими кінематиками пояснює тільки частину мінливості нейронної активності, яка спостерігається під час руху руки в просторі.[61][62]
Крім того, вектори популяції, побудовані на нейронній активності в М1, не завжди передбачують напрямок руху, як в класичних дослідженнях Георгопулоса. При вивченні рухів мавп у горизонтальній площині було виявлено, що вектори їхньої нейронної активності в М1 були зміщеними в бік одного з напрямків.[63] А довжина вектора популяції істотно змінювалася з напрямками руху, хоча самі рухи мали однакову величину та схожі піки швидкостей руки. Більшість напрямків руки не можна було передбачити через вектори популяції навіть використавши 18 різних способів їх побудови. Одна з причин неможливості вектора популяції передбачити напрямок руху в цьому дослідженні полягала в тому, що розподіл переважних напрямків нейронів не є одномірним: нейрони мають переважні напрямки або «від тіла і ліворуч», або ж «до тіла і праворуч».[64] Іншою причиною зміщення переважних напрямків нейронів є механічна анізотропія кінцівки: для генерації рухів кінцівок в цих двох напрямках потрібно більше механічного зусилля, аніж для рухів в інших двох декартових квадрантах.[65]
Кодування положення та швидкості руки в просторі
Окрім того, що нейронна активність в первинній моторній корі може кодувати відносно статичні кінематичні параметри руху (напрямок руху руки від точки до точки), вона також здатна репрезентувати параметри, які неперервно змінюються протягом прямолінійних рухів руки, як положення, швидкість та прискорення.
Свого часу, постулюючи проблему надлишковості ступенів свободи, російський радянський психофізіолог Микола Бернштейн зазначав, що нема єдиного й однозначного відношення між активацією м'яза та кінематикою руху руки.[66] Відомо, що нелінійне відношення між м'язовою активацією та генерованою ним м'язовою силою залежить як від поточної довжини м'яза, так і від швидкості його подовження.[67] Сили, викликані скороченням м'язів, генерують крутні моменти суглобів, які хоч і діють локально, призводять до прискорення суглобів всієї системи, що істотно змінюється з поточним положенням та швидкістю руки. Якимось чином ЦНС повинна «обчислювати» ці складні, нелінійні перетворення від активації м'язів до зміни положення руки в просторі, щоб вправно керувати рухами руки. Для того, аби точно обчислити м'язову активацію, ЦНС потрібна інформація про поточний стан скелетно-м'язової системи: положення руки та її швидкість.
Інформацію про поточне положення та (векторну) швидкість руки моторна кора може отримувати як через зорову систему, так і через пропріорецептори. У випадку пропріоцепції (відчуття положення частин тіла відносно один одного та їхнього руху), м'язове веретено вимірює положення руки та її швидкість та відсилає цю інформацію до спинного мозку. Однак, сам по собі, без залучення кори, ані спинний мозок, ані пропріоцепція не обчислюють перетворення м'язової активації в рух руки, оскільки пацієнти з міопатією м'язових волокон великого діаметра (відсутність пропріоцептивних імпульсів із веретен) можуть робити відносно точні рухи досягання за наявності зорової інформації.[68][69] Відтак, моторна кора може кодувати поточне положення та швидкість руки через зорову інформацію.
Характерною рисою руху руки в просторі є те, що її векторну швидкість може бути розкладено на скалярну швидкість та напрямок. Проте, як показали поведінкові дослідження рухів[70] та аналізовані в наступних розділах реєстрації нейронної активності in vivo, в М1 ці кінематичні параметри також кодуються окремо для рухів досягання. Тож моторна кора розрізняє між корелятивно поєднаними кінематичними параметрами і здатна керувати складними рухами багатосегментних кінцівок, кодуючи вищі моторні змінні.
В традиційних експериментах, вибірковість нейронів М1 до напрямку зазвичай оцінювали через одиничну частоту розрядів для кожного руху досягання. Однак, для виявлення неперервного зв'язку між параметрами руху та нейронною активністю необхідно знати, як ці параметри змінюються з часом. Траєкторія руху руки під час руху досягання є достатньо прямолінійною й напрямок руху є майже сталим. Тоді як швидкість руху руки, як виявили поведінкові дослідження, має форму куполоподібної кривої для найрізноманітніших завдань досягання[8][71] (Див. інтерактивну демонстрацію на Мал.3.9[72]), що дозволяє дослідникам порівняти швидкість із частотою розрядів нейрону протягом певного часу.
Регресійні моделі кодування положення та швидкості
Послідовність спайків (англ. spike train), реєстрована в М1 під час виконання рухів, не є регулярною між різними завданнями, та навіть в рамках одного й того ж завдання, тому в обчислювальній нейронауці її апроксимують як Пуассонівський процес. З огляду на цю мінливість генерування серії спайків для виявлення інформації, наявної в нейронній активності про моторні параметри, доречно використовувати ймовірнісні моделі кодування, які на відміну від моделей кривих налаштування (англ. tuning curves), беруть до уваги нейронну мінливість та шум.[73] Однією з таких імовірнісних моделей, яку широко використовують у моторній нейробіології, є лінійна регресійна модель, яка хоч і призначена для аналізу неперервних даних, після попередньої обробки цих даних може достовірно кодувати кінематичні змінні.[74]
Якщо є деякий експериментально спостережуваний сигнал (напр., рух), то постає завдання передбачити ймовірність появи послідовності спайків даного нейрону у відповідь на цей сигнал (напр., реакцію нейрону на швидкість руху руки в певному напрямку). Тобто, потрібно оцінити умовну ймовірність послідовності спайків за умови стимулу .
На прикладі М1, якщо це зріз положення та швидкості руки в час , тоді налаштованість нейрону моделюється через простий лінійний вираз
де позначує скалярний добуток між векторами і , — основна (середня) частота розрядів, а це 2D вектор, чия абсолютна величина відображає силу налаштованості нейрону і чий напрямок є «переважним напрямком» (виражається через синусоїдну (косинусну) криву налаштування).[75] Подібна модель досить добре передбачує частоту розрядів відповідно до деякого положення руки чи її руху з певною швидкістю, в певний проміжок часу.
Використавши метод множинної лінійної регресії, нейронауковці на чолі з Георгопулосом показали, що 3-вимірне положення кисті руки кодується нейронами М1 як скалярний добуток між вектором положенням кисті та «градієнтом положення» (англ. positional gradient), визначеним як вектор, в напрямку якого різниця в положенні кисті приводить до найбільшої різниці в нейронній активності.[76] Зокрема, 64 % із реєстрованих дослідниками нейронів проявляли лінійну залежність між тонічною частотою розрядів та положенням кисті, виражену через регресійне рівняння
- ,
де — це частота розряду нейрону в місцеположенні , а є коефіцієнтами регресії. Якщо, до прикладу, положення змінюватиметься тільки вздовж 1 із 3 осей координат, тоді частота розрядів буде лінійною функцією від положення в цій осі.
Згодом Георгопулос з колегами виявили, що хоча нейрони в М1 кодували положення кисті під час її руху в просторі, вони ще більше реагували на (векторну) швидкість кисті руки, тим самим одночасно кодуючи кілька моторних параметрів руху.[34] Інша група дослідників показала, що репрезентація кожного з цих параметрів в нейронній активності змінювалася протягом завдання рухів досягання: швидкість була домінуючим чинником в активності одиничного нейрону в середині завдання, тоді як положення було домінуючим наприкінці досягання, коли потрібне тримання постави руки.[28]
В серії оригінальних досліджень Ендрю Шварц (англ. Andrew B. Schwartz) з колегами виявили, що швидкість та напрямок руху (тобто, векторна швидкість) лінійно кодуються популяцією нейронів М1 не тільки в прямолінійних рухах досягання до цілі, але й в рухах малювання.[37][39][77]
Дослідники виявили, що напрямок та швидкість руху, які неперервно змінювались протягом рухів малювання та спірального відстежування цілі, активно впливали на нейронну активність в М1.[40][78] Отримані на основі цих кінематичних параметрів вектори популяції дозволяли точно передбачити складні траєкторії руху кисті руки в просторі.[38] Затримка в часі між нейронною активністю, вираженою через вектор популяції, та відповідним рухом зростала із збільшенням кривини шляху кисті руки в просторі. Тому регресійні моделі, які включали швидкість та напрямок руху (векторну швидкість), передбачували нейронну активність значно точніше за ті, які використовували лише напрямок руху.[37] Хоча апроксимація нейронної активності моделями, які включали ЕМГ сигнали чи швидкість кутів суглобів, схоплювала відносно меншу мінливість нейронних розрядів і не була такою точною, як моделі траєкторії руки.[38].
Цікаво, що було виявлено стійку кореляцію між часовим профілем нейронних розрядів в М1 та куполоподібною кривою швидкості руху руки. Це свідчило про те, що швидкість руху є одним з ключових моторних параметрів, які кодуються в М1.[37]
На основі цих досліджень кодування швидкості руху в М1 постала канонічна модель, яка лінійно пов'язувала частоту розрядів нейронів із швидкістю руху:
де — середня частота розрядів, — основна (вихідна) частота розрядів; — переважний напрямок нейрону; — швидкість руки в час , а — часова затримка між нейронною активністю в М1 та кінематикою руху (зазвичай, від 100 до 150 мс).[37]
Недоліки відцентрових завдань
Основною поведінковою парадигмою більшості попередніх досліджень було класичне відцентрове завдання: коли суб'єкт, тримаючи маніпуляндум чи з вільною рукою, робив рухи досягання від центру до кількох периферійних цілей в дво- чи тривимірному просторі. Однак це завдання має низку недоліків, які не дозволяють однозначно встановити, які саме параметри кодує М1.
Відцентрове завдання покрокового відстеження (англ. step-tracking task) уможливлюють тільки обмежений контроль над кінематичними параметрами, оскільки рух руки контролюється суб'єктом, а не експериментатором. Крім того, в таких завданнях обмежується розмір параметричного простору: дослідник обирає невелику фіксовану групу можливих локацій в просторі (найчастіше, 8), які, через необхідність зупинки руху біля вибраної цілі, призводять до майже прямолінійних, стереотипних рухів руки. Позаяк в такому завданні швидкість та положення руки надто сильно корелюють, то важко визначити їхній окремий внесок до розрядів нейронів М1.[61]
В ранніх дослідження нейронної активності в М1 поведінкові змінні трактували як статичні, скалярні величини (напр. середній напрямок руки чи скалярна швидкість), а корелюючу з ними й мінливу в часі нейронну активність підсумовували як єдине число — усереднену частоту розрядів. Дані нейронної активності усереднювали протягом різних випробувань і апроксимували високо-параметричними моделями налаштування (як косинусна функція), усуваючи потенційно багату, динамічну інформацію про індивідуальну нейронну активність, що накладало відбиток на той код нейронної популяції в М1, який отримувався в підсумку.[43][79] В пізніших дослідженнях часові аспекти кодування кінематики в М1 вже вивчали більш явно, трактуючи моторну кінематику та відповідну нейронну активність як мінливі в часі.[34][37] Однак в цих дослідженнях дослідники не змогли подолати статистичну залежність між змінними та плутали властивості, «залежні від часу» (англ. time-dependent), із «залежними від часової затримки» (англ. lag-dependent), де затримка — це відставання між нейронними спайками та їхнім проявом в моторній поведінці. Тому часова динаміка, яку виявляли ці дослідження, могла відображати часову еволюцію умов поведінкового завдання, а не основоположну нейронну динаміку кодування моторних параметрів.[61]
Окрім того, серійна техніка реєстрації нейронної активності, яку використовували в ранніх дослідженнях М1, унеможливлювала пряме порівняння кодування просторово-часових властивостей між нейронами, оскільки окремі одиниці реєстрували за поведінкових та станово-нейронних умов, які змінювались між різними випробуваннями протягом завдання, а відтак і між різними нейронами. Подібна серійна реєстрація призводила до припущення про статистичну незалежність між нейронами (оскільки залежність неможливо виявити без одночасної реєстрації популяції нейронів), що однак було спростоване новітніми даними.[80][81]
Завдання випадкового супроводжувального відстежування
З метою усунути недоліки класичних поведінкових «відцентрових» завдань та відокремити корельовані моторні параметри в нейронній активності, Панінські та ін. досліджували просторово-часове кодування руху використовуючи запропоноване Ліамом Панінські (англ. Liam Paninski) оригінальне поведінкове завдання випадкового, неперервного супроводжувального відстежування (англ. pursuit-tracking task, PTT).[61] Цей психофізичний метод значно краще підходив для вивчення окремих моторних параметрів і згодом широко використовувався для вивчення природи нейронного кодування в моторній корі.[82][83][84][85][86]
Завдання PTT навмисно було організовано таким чином, щоб виділити просторові та часові характеристик нейронів М1, одночасно мінімізуючи статистичні залежності та мінливості, притаманні завданням з відцентровими рухами. Дослідники навчили трьох мавп неперервно відстежувати візуальну ціль, що плавно та випадково рухалася на комп'ютерному моніторі, та в рухати в її напрямку маніпуляндум, що обмежував рух кисті горизонтальною площиною. На початку кожного випробування з'являлася візуальна ціль у випадковому місці, вибрана із двовимірного, нуль-коваріаційного розподілу Ґауса із середнім, розміщеним по центру операційного простору. Кожне положення цілі (а тому і положення кисті руки, яка з маніпуляндумом за нею слідувала) було випадково генерованим (через Гаусів білий шум) сигналом, що з'являвся тільки один раз.[61]
Таке відстежування випадкової цілі найкраще підходило для вивчення кодування в М1 положення та швидкості руху. В завданні PTT траєкторію кисті трактували як випадковий «стимул» до моторної системи, а нейронну активність — як «реакцію» системи на нього. Експериментатор вибирав кожен стимул із визначеного ним розподілу стимулів, який неперервно і широко покривав простір швидкості та положення, і був стаціонарним відносно часу випробування. Відтак, дослідник може ефективно впливати на рух мавпою кисті та зменшувати статистичні залежності між моторними параметрами.
Розподілена репрезентація швидкості та положення в М1
Статистичні властивості завдання PTT дозволили Панінські та ін. застосувати методи теорії інформації та обробки сигналів для аналізу кодування положення та швидкості. А мультиелектродна реєстрація, використана дослідниками, уможливлювала порівняння кодування моторних параметрів між кількома нейронами. На основі PTT, методів лінійної регресії та інформаційної теорії, Панінські та ін. виявили, що положення та швидкість кисті руки одночасно кодуються одиничними нейронами М1, хоча також були нейрони, які кодували положення окремо від швидкості.[61] Криві нейронного налаштування до положення та часу, виражені через косинусні функції, модулювались (англ. gain-modulated) скалярною швидкістю та відстанню.
Дослідники також показали, що з невеликого ансамблю випадково вибраних нейронів (від 3 до 19 нейронів) в області руки в М1 можливо реконструювати випадкові, двовимірні траєкторії кисті руки. При тому, що включення в реконструкцію нейронних даних після настання руху покращувало декодування траєкторії, вказуючи на те, що М1 кодує окрім прямого сигналу руху також і зворотну копію поточного руху руки.
З допомогою іформаційно-теоретичного аналізу Панінські та ін. виявили, що невелика частота розрядів нейронів М1 містила достатньо інформації про положення та швидкість, а реєстровані нейрони характеризувалися значним різноманіттям у змісті кодованої ними інформації. Це вказувало на розподілену репрезентацію цієї кінематичної інформації серед нейронів М1 і на те, що вона може бути повністю репрезентованою в невеликій області в М1.[61]
В цілому ж, нейрони в М1 містили невелику кількість інформації про положення та швидкість, проявляючи слабку, хоча й статистично значущу, кореляцію між інформацією про швидкість та положення. Що свідчило про те, що нейрони М1 прямо кодували змінні, які опосередковано були пов'язаними з положенням та швидкістю руху руки.
Адитивне та мультиплікативне кодування положення і обертання
Поєднавши експериментальні методи та регресійні моделі попередніх досліджень, група нейронауковців на чолі з Деніелом Мораном (англ. Daniel W. Moran) показала, що положення та швидкість одночасно, в адитивний спосіб, кодуються одиничними нейронами в М1, як протягом статичних завдань, так і протягом рухів досягання.[87] Однак швидкість, а не положення, більше модулювала нейронну активність під час рухів досягання. Розроблений дослідниками на основі алгоритму вектора популяції новий метод декодування («непряма оптимальна лінійна оцінка», англ. indirect optimal linear estimator, OLE) дозволив одночасно реконструювати 3D положення та 3D швидкість кисті руки із нейронної активності моторної кори. Завдяки цьому методу було виявлено, що сигнал положення та сигнал швидкості різняться в затримці між їхньою репрезентацією в корі та їхнім виконанням в рухові руки: нейронний сигнал швидкості випереджав реальну швидкість кисті на 122 мс, а сигнал положення реальне положення — на 81 мс.
Ця ж група на чолі з Мораном пізніше виявила, що одиничні нейрони М1 навіть можуть одночасно кодувати положення, орієнтацію та їхні похідні за часом — поступальну і обертальну швидкості кисті руки; хоча обертальна швидкість кисті сильніше модулювала нейронну активність, аніж її орієнтація.[88]
Дослідники показали, що кодування одиничними нейронами двох чи більше з цих кінематичних змінних було нелінійним і відбувалось не лише в адитивний спосіб, але й у мультиплікативний, подібно до кодування поля підсилення, (англ. gain-field encoding). У випадку нейронного кодування поля підсилення в М1 косинусні криві поступального налаштування модулювались обертальною швидкістю руки. На основі цього відкриття науковцями було запропоновано загальну модель кодування моторною корою 3-вимірних положення, орієнтації, поступальної та обертальної швидкостей:
де — це загальна нейронна активність; і — середня нейронна активність, пов'язана, відповідно, з переміщенням та обертанням кисті руки; — це вектор , який репрезентує як переважний напрямок, так і переважний «градієнт положення» нейрону, є вектором , що репрезентує як обертальну швидкість, так і положення кисті в просторі (); — це вектор , який репрезентує одночасно переважне обертання та переважний «градієнт обертання» нейрону, а є вектором , що репрезентує обертальну швидкість та орієнтацію кисті в просторі ().[88]
Існування в моторній корі подібної популяції нейронів, що кодує одночасно паралельне перенесення та обертання не є випадковим з точки зору біомеханіки, оскільки рух скелетно-м'язової системи руки описується множиною диференціальних рівнянь другого порядку, в яких паралельне перенесення та обертання є динамічно пов'язаними і тому повинні разом плануватись під час виконання руху. Відтак, первинна моторна кора кодує кінематику руки.
Кодування траєкторії руху
Нелінійне кодування траєкторії в М1
Лінійні моделі, побудовані на основі регресійних методів, досить добре передбачують частоту нейронних розрядів на основі певного положення чи швидкості руки в певний обмежений проміжок часу. Однак ці моделі не в змозі передбачити нейронну поведінку для різних проміжків часу, в яких змінюється траєкторія руки, і вони не враховують вплив сусідніх нейронів М1 на активність даного нейрона в кодуванні моторних параметрів. Складність передбачування полягає в тому, що потрібно оцінити ймовірність спайків не над 2-D просторами всіх можливих положень та швидкостей, але над більш високо-розмірним простором всіх можливих траєкторій руки та поведінки нейронної мережі в М1.
Для розв'язання цієї проблеми Панінські та ін.[62] запропонували поширену в сенсорній нейробіології ймовірнісну, лінійну-нелінійну каскадну модель.[75][89]
Ймовірнісні «каскадні» моделі складаються із двох етапів: 1) лінійного фільтра, в якому спостережуваний сигнал проєктується на низькорозмірний підпростір; цей етап відповідає просторово-часовому «рецептивному полю» нейрона, ефективно репрезентуючи відповідну інформацію, що міститься у (високо-розмірному) вхідному сигналі; 2) етап нелінійного, ймовірнісного генерування спайку. Найпоширенішим типом таких каскадних моделей є «лінійна-нелінійна Пуассонівська каскадна модель», в якій спайки генеруються відповідно до неоднорідного Пуассонівського процесу і чия частота появи визначається миттєвою нелінійною функцією лінійно фільтрованого вхідного сигналу.[90][91]
Каскадна модель Панінські та ін. була узагальненням лінійної регресійної моделі (див. попередній розділ) та описувала вплив мінливої в часі траєкторії кисті руки та стану нейронної мережі М1 на активність одиничних нейронів М1:
де скалярний добуток виражає залежність активності нейрону від траєкторії кисті руки й відповідає операції лінійного фільтра, застосованого до вектора траєкторії руки ; фільтр отримує з траєкторії руки максимальну інформацію про частоту розрядів нейронів, постаючи як переважний напрямок нейрону; — це залежність активності нейрону від активності сусідніх нейронів в нейронній мережі М1, де — вектор кількості спайків одночасно реєстрованих сусідніх нейронів М1; — вектор нейронної зваженості, з як вага, призначена нейрону .[62]
В цій каскадній моделі спочатку (а) сигнал положення руки лінійно фільтрується переважною траєкторією , тоді як активності сусідніх нейронів М1 лінійно зважуються вектором ваг для отримання кінематично () та нейронно () відфільтрованих сигналів; потім (б) ці фільтровані сигнали сумуються і до суми застосовується нелінійна, експоненційна функція кодування , яка генерує передбачену частоту розрядів нейронів М1.
Лінійно-нелінійна каскадна модель дозволила Панінські та ін. показати, що нейрони М1 надлінійно (нелінійно) кодують цілісну траєкторію руки протягом всього часу, а не тільки швидкість, положення чи прискорення руки в певний проміжок часу. Нелінійна «переважна траєкторія» набагато краще передбачувала нейронну активність, аніж положення й швидкість. Цю нелінійність могло бути апроксимовано через просту експоненційну модель, що звужувала, порівняно з косинусною, направлену налаштованість нейронів М1 та приводила до модульованого підсилення — коли залежність нейронної активності від швидкості модулюється, майже мультиплікативно, положенням руки. Тобто, навіть незначна зміна положення може істотно модулювати підсилення налаштованості нейронів М1 на швидкість руки.[62]
Крім того, з допомогою каскадної моделі дослідники виявили, що активність сусідніх нейронів в М1-нейронній мережі має значно більший вплив на частоту розрядів даного нейрону, ніж припускали регресійні моделі одночасного кодування швидкості та положення руки, й тому дозволяє істотно покращити передбачення частоти розрядів одиничних нейронів М1. Це відкриття підтверджувало результати інших досліджень про інформаційну надлишковість в М1, де нейрони містять значну кількість інформації про корельовану популяційну активність сусідніх нейронів.[84] Однак нейрони М1 є корельованими не тому, що їхні криві налаштування збігаються чи через інтеренйронну взаємодію, як припускали попередні дослідження.[81][92] Причиною кореляції в М1 є, скоріш за все, спільні джерела вхідних сигналів, які кодують складні функції кінематики траєкторії руху.[62]
Тож, подібно до зорової кори та гіпокампа, активність нейронів в моторній корі залежить від активності сусідніх нейронів, і тому розуміння активності даного одиничного нейрону М1 потребує включення цього взаємозв'язку між нейронами поряд з їхньою налаштованістю на зовнішні моторні параметри.
Кодування фрагментів руху
На відміну від поширеного в моторній нейрофізіології з 1970-х років погляду, що моторна кора кодує окремі, незалежні від часу кінематичні/кінетичні змінні руху, видатний британський фізіолог сер Чарлз Скотт Шеррінгтон ще 1917 року висунув гіпотезу, що одиничні нейрони в моторній корі репрезентують елементарні поведінкові фрагменти рухів, а не їхні окремі параметри.[93][94]
Частково підтверджуючи погляди Шеррінгтона, кілька експериментальних досліджень показали, що електрична мікростимуляція первинної моторної кори може викликати складні, змінювані з часом рухи, які є частиною координованої моторної поведінки.[95][96][97] Крім того, в серії нейрофізіологічних досліджень було показано, що направлена налаштованість нейронів М1, виявлена Георгопулосом та ін., не є незмінною в часі й суттєво зміщується протягом виконання простих рухів досягання (див. докладніше).[98][99] В дослідженні нейронної активності одночасно в М1, додаткової моторної області та дорсально-вентральних областях премоторної кори під час різних типів рухів досягання мавпою, було виявлено, що нейрони активізуються переважно щодо конкретних типів шляхів кисті руки в просторі, навіть коли початкові та кінцеві положення цих шляхів були однаковими.[100] На основі цього дослідження було висунуто припущення, що нейрони моторної кори кодують не окремі кінематичні параметри (напрямок, швидкість чи прискорення руху, положення в просторі), а абстрактніші форми руху, як кривину і шлях руки в просторі.
В оригінальному дослідженні Ніколаса Хатсопулоса (англ. Nicholas Hatsopoulos) та ін. вперше було експериментально підтверджено припущення, що одиничні нейрони М1 кодують складні, залежні від часу траєкторії руху, і запропоновано модель, як саме нейрони М1 кодують такі траєкторії.[101]
Хатсопулос та ін. навчили трьох мавп виконувати два типи завдань. В одному завданні (відстежування випадкової цілі) мавпа повинна була досягати до послідовності 7-и випадково розміщених цілей, рухаючи до них на площині екзоскелетну роботизовану дво-сегментну руку, яка контролювала курсор. Це завдання дозволяло суб'єкту генерувати значне різноманіття траєкторій та шляхів, з різними просторовими формами, швидкостями та положеннями руки, подібно до експериментів у сенсорній нейрофізіології з білим шумом, за допомогою якого вивчається налаштованість до конкретних параметрів нейронів у сенсорних системах. В цьому ж завданні через екзоскелет, на якому знаходилася рука мавпи, було прикладено навантаження до суглобів плеча та ліктя для вивчення того, які саме параметри кодує М1. Інше завдання було класичним, стереотипним відцентровим досяганням до 8 периферійних цілей, і виконувалось одразу після першого завдання.
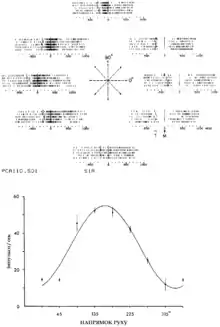
У відцентровому завданні дослідники виявили систематичні зміщення в «переважному напрямку» одиничних нейронів М1 на 90° і протягом понад 400 мс (від 100 мс до — і 300 мс під час настання руху). Однак такі самі зміщення і з такою ж тривалістю дослідники зафіксували і в завданні відстежування випадкових цілей. Позаяк такі систематичні зміщення в переважних напрямках були схожими в різних частинах операційного простору та в двох протилежних завданнях, науковці припустили, що нейрони М1 кодують не якийсь окремий, незмінний в часі параметр руху (напр., швидкість), а змінювані в часі, складні траєкторії швидкості, т. зв. «переважні траєкторії». Оскільки ці траєкторії включали залежну від часу швидкість руху, то вони містили одночасно інформацію про напрямок та відносну швидкість руху.[101]
З ціллю показати, що змінювані в часі траєкторії дійсно характеризують налаштованість нейрону, Хатсопулос та ін. побудували узагальнену лінійну модель, яка оцінювала ймовірність генерування спайку нейроном за умови, якщо кисть руки мавпи слідуватиме певною траєкторією швидкості. Як і в дослідженні Панінські та ін.,[62] отримані дані найкраще були апроксимовані моделлю, яка включала експоненціальне відношення між ймовірністю спайку і скалярним добутком «переважної траєкторії» швидкості () та нормалізованої траєкторії швидкості руки ():
де кожна траєкторія швидкості охоплює діапазон часових відрізків перед- і після настання спайку, ; — це параметр зміщення моделі; — послідовність швидкостей (тобто, напрямків та відносних скалярних швидкостей) протягом визначеної тривалості часу.
«Переважна траєкторія» швидкості даного нейрону характеризувалась залежними від часу змінами в - та -вимірах руху. Трактуючи кожний переважний напрямок даного нейрону як вектор швидкості одиничної довжини та інтегруючи за часом окремо - та -компоненти переважної траєкторії швидкості, Хатсопулос та ін. отримали складні форми «переважних шляхів» (англ. pathlets) для кожного нейрону. Тому модель, побудована на основі кодування нейронами М1 розширених в часі переважних траєкторій руху, точніше передбачала появу чи відсутність спайку одиничного нейрону, аніж моделі з коротшими траєкторіями, що мали незалежні від часу переважні напрямки.[101]
Для того, щоби перевірити, які саме параметри, кінетичні чи кінематичні, кодує М1, Хатсопулос та ін. застосували цю експоненціальну модель для передбачування ймовірності спайків на основі розширеної в часі траєкторії крутного моменту плеча та ліктя. Як і у випадку з переважною траєкторією швидкості, «pathlet» крутного моменту тривалістю 400 мс оптимально передбачував появу спайку. Разом з тим, під час завдання з відстежуванням випадкової цілі, коли до суглобів плеча та ліктя мавпи через екзоскелет прикладалось навантаження, реєстровані нейрони в М1 сильніше кодували кінематичні, аніж кінетичні параметри: нейрони проявляли відносно незмінні переважні траєкторії швидкості та відповідні pathlets, тоді як їхні переважні траєкторії крутних моментів сильніше змінювались, як під час навантажень, так і за їх відсутності. Це вказувало на те, що первинна моторна кора кодує рух у формі складних кінематичних, а не кінетичних траєкторій. Хоча незалежно від системи координат, в якій оперує М1, складні, залежні від часу траєкторії (як кінематичні, так і кінетичні) набагато точніше передбачували ймовірність генерування одиничним нейроном спайку, аніж незалежні від часу, прості моторні параметри.
Для підтвердження, що нейрони М1 дійсно кодують фрагменти рухів, Хатсопулос та ін. також побудували алгоритм нейронного декодування, який включав залежну від часу траєкторію для кожного нейрону. Цей алгоритм точніше передбачував напрямок руху, аніж стандартний алгоритм, що включав незмінний в часі переважний напрямок руху. Помилка передбачення напрямку була на 10° меншою при використанні множини переважних напрямків тривалістю 400 мс у порівнянні з підходом традиційного вектора популяції, який використовує переважні напрямки між +100 мс та +150 мс.[101]
Відкриття Хатсопулосом та ін. кодування одиничними нейронами М1 залежної від часу траєкторії руху («переважних шляхів») розв'язувало низку класичних проблем моторної нейрофізіології. Зокрема, концепція кодування складної траєкторії узгоджується із зміщенням переважних напрямків в часі, яке часто спостерігається в традиційному відцентровому завданні до (під час навченої затримки) та протягом виконання руху. Хоча моделі моторного керування, які припускали, що нейрони М1 кодують силу, генеровану м'язами під час активізації кінцівки (див. докладніше), пояснювали ці зміщення із впливом навантаження на рух руки, існування цього зміщення під час навченої затримки (в підготовчому стані, до виконання руху) виключає вплив навантаження на зміщення переважних напрямків.
Крім того, кодування залежної від часу траєкторії вдало пояснює те, чому в різних дослідженнях було виявлено різні кінематичні параметри, які кодують нейрони М1 — напрямок, швидкість, прискорення і положення. Оскільки моторна кора репрезентує фрагменти руху, які включають багато параметрів, залежних від часу, то протягом реєстрації й під час різних поведінкових завдань даний нейрон проявлятиме складну поведінку, що узгоджуватиметься в різних дослідженнях з усіма абстрактними кінематичним параметрами, які вивчаються.
Тож відкриті Хатсопулосом та ін. переважні шляхи (pathlets), які кодують одиничні нейрони, можуть бути базисними моторними одиницями, з яких формується складніша моторна поведінка.
Не зважаючи на те, що нейронауковці продовжують дебатувати щодо інтерпретації моторно-кортикальних нейронних кореляцій руху в просторі та ставити під сумнів пояснювальну силу таких кореляцій,[102][103][104][105][106][107] вони надалі залишаються привабливими в нейробіології, оскільки безпосередньо пов'язують нейронну активність з ключовими рисами моторної поведінки та дозволяють побудувати нейро-комп'ютерні інтерфейси, які допомагають відновити прості рухи паралізованих пацієнтів.[17][108][109]
Див. також
Примітки
- 1) ↑ Пізніші експериментальні дослідження Георгопулоса та ін. показали, що криві направленого налаштування можуть бути вужчими, аніж косинусна функція, і змінюватись як розподіл фон Мізеса в одиничному колі, тому краще описуються експоненційною функцією фон Мізеса, яка на відміну від косинусної функції дозволяє варіацію в ширині направленого налаштування[110][111] Втім, косинусна функція є найпростішою з фунцій, яка пояснює значний відсоток мінливості в активності нейрона і тому добре підходить для опису залежності частоти розрядів нейронів від напрямку руху
Джерела
- Evarts EV (1966). Pyramidal tract activity associated with a conditioned hand movement in the monkey. Journal of Neurophysiology 29 (6): 1011–27. PMID 4961643.
- Evarts, E.V. (1968). Relation of pyramidal tract activity to force exerted during voluntary movement. Journal of Neurophysiology 31 (1): 14–27. PMID 4966614.
- Humphrey D. R., Schmidt E. M. and Thompson W. D. (1970). Predicting Measures of Motor Performance from Multiple Cortical Spike Trains. Science 170 (3959): 758–762. ISSN 0036-8075. doi:10.1126/science.170.3959.758.
- Humphrey Donald R. (1972). Relating motor cortex spike trains to measures of motor performance. Brain Research 40 (1): 7–18. ISSN 00068993. doi:10.1016/0006-8993(72)90099-6.
- Zernicke R.F. & Smith J.L. (1996). Biomechanical Insights into Neural Control of Movement. У Rowell L.B. & Shepherd J.T. Handbook of Physiology. Section 12: Exercise: Regulation and Integration of Multiple Systemsn. Oxford. с. 293–330. doi:10.1002/cphy.cp120108.
- Burdet E., Franklin D.W. & Milner T.E. (2013). Human Robotics: Neuromechanics and Motor Control. MIT Press. с. 277. ISBN 9780262019538.
- Hollerbach John M. & Flash Tamar (1982). Dynamic interactions between limb segments during planar arm movement. Biological Cybernetics 44 (1): 67–77. ISSN 0340-1200. doi:10.1007/BF00353957.
- Soechting JF & Lacquaniti F (1981). Invariant characteristics of a pointing movement in man. The Journal of Neuroscience 1 (7): 710–20. PMID 7346580.
- Mountcastle VB, Lynch JC, Georgopoulos A, Sakata H and Acuna C (1975). Posterior parietal association cortex of the monkey: command functions for operations within extrapersonal space. Journal of Neurophysiology 38 (4): 871–908. PMID 808592.
- Georgopoulos A.P., Kalaska J.F., Caminiti R. and Massey J.T. (1982). On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. The Journal of Neuroscience 11 (2): 1527–1537. PMID 7143039.
- Kalaska JF, Cohen DA, Hyde ML and Prud'homme M (1989). A comparison of movement direction-related versus load direction-related activity in primate motor cortex, using a two-dimensional reaching task. The Journal of Neuroscience 9 (6): 2080–2102. PMID 2723767.
- Schwartz A.B., Kettner R.E. and Georgopoulos A.P. (1988). Primate motor cortex and free arm movements to visual targets in threedimensional space. I. Relations between single cell discharge and direction of movement. The Journal of Neuroscience 8 (8): 2913–2927. PMID 3411361.
- Caminiti R, Johnson PB and Urbano A (1990). Making arm movements within different parts of space: dynamic aspects in the primate motor cortex. The Journal of Neuroscience 10 (7): 2039–2058. PMID 2376768.
- Georgopoulos A., Schwartz A. and Kettner R. (1986). Neuronal population coding of movement direction. Science 233 (4771): 1416–1419. ISSN 0036-8075. doi:10.1126/science.3749885.
- Schwartz Andrew B., Taylor Dawn M. and Tillery Stephen I. Helms (2001). Extraction algorithms for cortical control of arm prosthetics. Current Opinion in Neurobiology 11 (6): 701–708. ISSN 09594388. doi:10.1016/S0959-4388(01)00272-0.
- Taylor Dawn M., Tillery Stephen I. Helms and Schwartz Andrew B. (2002). Direct Cortical Control of 3D Neuroprosthetic Devices. Science 296 (5574): 1829–1832. ISSN 00368075. doi:10.1126/science.1070291.
- Waldert Stephan, Pistohl Tobias, Braun Christoph, Ball Tonio, Aertsen Ad and Mehring Carsten (2009). A review on directional information in neural signals for brain-machine interfaces. Journal of Physiology-Paris 103 (3-5): 244–254. ISSN 09284257. doi:10.1016/j.jphysparis.2009.08.007.
- Georgopoulos A.P., Kalaska J.F., Crutcher M.D., Caminiti R. and Massey J. T. (1984). Chapter 16. The representation of movement direction in the motor cortex: single cell and population studies. У Edelman G. M., Gall W. E. and Cowan W. M. Dynamic Aspects of Neocortical Function. Wiley. с. 501–524. ISBN 9780471805595.
- Georgopoulos A.P., Crutcher M.D. and Schwartz A.B. (1989). Cognitive spatial-motor processes. Experimental Brain Research 75 (1). ISSN 0014-4819. doi:10.1007/BF00248541.
- Smyrnis Nikolaos, Taira Masato, Ashe James and Georgopoulos Apostolos P. (1992). Motor cortical activity in a memorized delay task. Experimental Brain Research 92 (1). ISSN 0014-4819. doi:10.1007/BF00230390.
- Velliste M., Perel S., Spalding M.C., Whitford A.S. & Schwartz A.B. (2008). Cortical control of a prosthetic arm for self-feeding. Nature 453 (7198): 1098–1101. ISSN 0028-0836. doi:10.1038/nature06996.
- Georgopoulos A.P., Kettner R.E. and Schwartz A.B. (1988). Primate motor cortex and free arm movements to visual targets in three- dimensional space. II. Coding of the direction of movement by a neuronal population. The Journal of Neuroscience 8 (8): 2928–2937. PMID 3411362.
- Lukashin A. V., Amirikian B.R., Mozhaev V. L., Wilcox G. L. and Georgopoulos A. P. (1996). Modeling motor cortical operations by an attractor network of stochastic neurons. Biological Cybernetics 74 (3): 255–261. ISSN 0340-1200. doi:10.1007/BF00652226.
- Georgopoulos A., Lurito J., Petrides M., Schwartz A. and Massey J. (1989). Mental rotation of the neuronal population vector. Science 243 (4888): 234–236. ISSN 0036-8075. doi:10.1126/science.2911737.
- Lurito J.T., Georgakopoulos T. and Georgopoulos A.P. (1991). Cognitive spatial-motor processes. Experimental Brain Research 87 (3). ISSN 0014-4819. doi:10.1007/BF00227082.
- Cohen D.A., Prud'homme M.J. and Kalaska J.F. (1994). Tactile activity in primate primary somatosensory cortex during active arm movements: correlation with receptive field properties. Journal of Neurophysiology 71 (1): 161–172. PMID 8158225.
- Kalaska J.F., Caminiti R. and Georgopoulos A.P. (1983). Cortical mechanisms related to the direction of two-dimensional arm movements: relations in parietal area 5 and comparison with motor cortex. Experimental Brain Research 51 (2). ISSN 0014-4819. doi:10.1007/BF00237200.
- Fu Q.G., Flament D., Coltz J.D. and Ebner T.J. (1995). Temporal encoding of movement kinematics in the discharge of primate primary motor and premotor neurons. Journal of Neurophysiology 73 (2): 836–854. PMID 7760138.
- Fortier, P. A., Smith, A. M. & Kalaska, J. F. (1993). Comparison of cerebellar and motor cortex activity during reaching: directional tuning and response variability. Journal of Neurophysiology 69 (4): 1136–1149. PMID 8492153.
- Bosco G. and Poppele R.E. (2003). Modulation of Dorsal Spinocerebellar Responses to Limb Movement. II. Effect of Sensory Input. Journal of Neurophysiology 90 (5): 3372–3383. ISSN 0022-3077. doi:10.1152/jn.00204.2003.
- Jones Kelvin E., Wessberg Johan and Vallbo Ake B. (2001). Directional tuning of human forearm muscle afferents during voluntary wrist movements. The Journal of Physiology 536 (2): 635–647. ISSN 00223751. doi:10.1111/j.1469-7793.2001.0635c.xd.
- Ribot-Ciscar E, Bergenheim M, Albert F, Roll JP (2003). Proprioceptive population coding of limb position in humans. Experimental brain research 149 (4): 512–519. PMID 12677332. doi:10.1007/s00221-003-1384-x.
- Scott, S. H. and Kalaska, J. F (1997). Reaching movements with similar hand paths but different arm orientations. I. Activity of individual cells in motor cortex. Journal of neurophysiology 77 (2): 826–852. PMID 9065853.
- Ashe James and Georgopoulos Apostolos P. (1994). Movement Parameters and Neural Activity in Motor Cortex and Area 5. Cerebral Cortex 4 (6): 590–600. ISSN 1047-3211. doi:10.1093/cercor/4.6.590.
- Fu Q-G, Suarez JI, Ebner TJ (1993). Neuronal specification of direction and distance during reaching movements in the superior precentral premotor area and primary motor cortex of monkeys. Journal of neurophysiology 70 (5): 2097–2116. PMID 8294972.
- Koike Yasuharu, Hirose Hideaki, Sakurai Yoshio, and Iijima Toshio (2006). Prediction of arm trajectory from a small number of neuron activities in the primary motor cortex. Neuroscience Research 55 (2): 146–153. ISSN 01680102. doi:10.1016/j.neures.2006.02.012.
- Moran DW and Schwartz AB (1999). Motor cortical representation of speed and direction during reaching. Journal of neurophysiology 82 (5): 2676–2692. PMID 10561437.
- Moran DW and Schwartz AB (1999). Motor cortical activity during drawing movements: population representation during spiral tracing. Journal of neurophysiology 82 (5): 2693–704. PMID 10561438.
- Schwartz AB (1993). Motor cortical activity during drawing movements: population representation during sinusoidal tracing. Journal of neurophysiology 70 (1): 28–36. PMID 8360717.
- Schwartz A. (1994). Direct cortical representation of drawing. Science 265 (5171): 540–542. ISSN 0036-8075. doi:10.1126/science.8036499.
- Georgopoulos A., Taira M. and Lukashin A. (1993). Cognitive neurophysiology of the motor cortex. Science 260 (5104): 47–52. ISSN 0036-8075. doi:10.1126/science.8465199.
- Georgopoulos Apostolos P. (1995). Current issues in directional motor control. Trends in Neurosciences 18 (11): 506–510. ISSN 01662236. doi:10.1016/0166-2236(95)92775-L.
- Sanger Terence D. (1994). Theoretical Considerations for the Analysis of Population Coding in Motor Cortex. Neural Computation 6 (1): 29–37. ISSN 0899-7667. doi:10.1162/neco.1994.6.1.29.
- Fetz Eberhard E. (1992). Are movement parameters recognizably coded in the activity of single neurons?. Behavioral and Brain Sciences 15 (Special issue 4): 679– 690. doi:10.1017/S0140525X00072599.
- Kalaska John F. (2009). From Intention to Action: Motor Cortex and the Control of Reaching Movements. У Sternad Dagmar. Progress in Motor Control. A Multidisciplinary Perspective 629. с. 139–178. ISSN 0065-2598. doi:10.1007/978-0-387-77064-2_8.
- Georgopoulos Apostolos P. (1996). On the translation of directional motor cortical commands to activation of muscles via spinal interneuronal systems. Cognitive Brain Research 3 (2): 151–155. ISSN 09266410. doi:10.1016/0926-6410(95)00040-2.
- Scott Stephen H. (2004). Optimal feedback control and the neural basis of volitional motor control. Nature Reviews Neuroscience 5 (7): 532–546. ISSN 1471-003X. doi:10.1038/nrn1427.
- Fukson O., Berkinblit M. and Feldman A. (1980). The spinal frog takes into account the scheme of its body during the wiping reflex. Science 209 (4462): 1261–1263. ISSN 0036-8075. doi:10.1126/science.7403886.
- d'Avella Andrea, Saltiel Philippe and Bizzi Emilio (2003). Combinations of muscle synergies in the construction of a natural motor behavior. Nature Neuroscience 6 (3): 300–308. ISSN 10976256. doi:10.1038/nn1010.
- McKiernan, B.J., Marcario, J.K., Karrer, J.H. and Cheney, P.D. (1998). Corticomotoneuronal postspike effects in shoulder, elbow, wrist, digit, and intrinsic hand muscles during a reach and prehension task. Journal of Neurophysiology 80 (4): 1961–1980. PMID 9772253.
- Cheney PD and Fetz EE (1980). Functional classes of primate corticomotoneuronal cells and their relation to active force. Journal of neurophysiology 44 (4): 773–91. PMID 6253605.
- Shinoda Yoshikazu, Yokota Jun-Ichi and Futami Takahiro (1981). Divergent projection of individual corticospinal axons to motoneurons of multiple muscles in the monkey. Neuroscience Letters 23 (1): 7–12. ISSN 03043940. doi:10.1016/0304-3940(81)90182-8.
- Lemon R.N., Mantel G.W. and Muir R.B. (1986). Corticospinal facilitation of hand muscles during voluntary movement in the conscious monkey.. The Journal of Physiology 381 (1): 497–527. ISSN 00223751. doi:10.1113/jphysiol.1986.sp016341.
- Ashe James (2004). Chapter 5. What Is Coded in the Primary Motor Cortex?. У Riehle Alexa and Vaadia Eilon. Motor Cortex in Voluntary Movements. A Distributed System for Distributed Functions. 20044553. ISSN 2154-5723. doi:10.1201/9780203503584.ch5.
- Mussa-Ivaldi F.A. (1988). Do neurons in the motor cortex encode movement direction? An alternative hypothesis. Neuroscience Letters 91 (1): 106–111. ISSN 03043940. doi:10.1016/0304-3940(88)90257-1.
- Burnod Y., Grandguillaume P., Otto I., Ferraina S., Johnson PB and R Caminiti (1992). Visuomotor transformations underlying arm movements toward visual targets: a neural network model of cerebral cortical operations. The Journal of Neuroscience, 12 (4): 1435–1453.
- Bullock Daniel, Grossberg Stephen and Guenther Frank H. (1993). A Self-Organizing Neural Model of Motor Equivalent Reaching and Tool Use by a Multijoint Arm. Journal of Cognitive Neuroscience 5 (4): 408–435. ISSN 0898-929X. doi:10.1162/jocn.1993.5.4.408.
- Gottlieb Gerald L. (1993). A Computational Model of the Simplest Motor Program. Journal of Motor Behavior 25 (3): 153–161. ISSN 0022-2895. doi:10.1080/00222895.1993.9942046.
- Todorov Emanuel (2000). Direct cortical control of muscle activation in voluntary arm movements: a model. Nature Neuroscience 3 (4): 391–398. ISSN 10976256. doi:10.1038/73964.
- Bennett K. M. and Lemon R. N. (1996). Corticomotoneuronal contribution to the fractionation of muscle activity during precision grip in the monkey. Journal of Neurophysiology 75 (5): 1826–1842. PMID 8734583.
- Paninski Liam, Fellows Matthew R., Hatsopoulos Nicholas G. and Donoghue John P. (2004). Spatiotemporal Tuning of Motor Cortical Neurons for Hand Position and Velocity. Journal of Neurophysiology 91 (1): 515–532. ISSN 0022-3077. doi:10.1152/jn.00587.2002.
- Paninski Liam, Shoham Shy, Fellows Matthew R., Hatsopoulos Nicholas G. and John P. Donoghue (2004). Superlinear Population Encoding of Dynamic Hand Trajectory in Primary Motor Cortex. Journal of Neuroscience 24 (39): 8551–8561. ISSN 0270-6474. doi:10.1523/JNEUROSCI.0919-04.2004.
- Scott Stephen H., Gribble Paul L., Graham Kirsten M. and Cabel D. William (2001). Dissociation between hand motion and population vectors from neural activity in motor cortex. Nature 413 (6852): 161–165. ISSN 00280836. doi:10.1038/35093102.
- Mitsuda Takashi and Onorati Paolo (2002). Three-dimensional tuning profile of motor cortical activity during arm movements. Neuroreport 13 (11): 1477–1480. ISSN 0959-4965. doi:10.1097/00001756-200208070-00026.
- Graham KM, Moore KD, Cabel DW, Gribble PL, Cisek P and Scott SH (2003). Kinematics and Kinetics of Multijoint Reaching in Nonhuman Primates. Journal of Neurophysiology 89 (5): 2667–2677. ISSN 0022-3077. doi:10.1152/jn.00742.2002.
- Бернштейн Николай Александрович (1990). Физиология движений и активность. Наука.
- Zajac FE (1989). Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Critical Reviews in Biomedical Engineering 17 (4): 359–411. PMID 2676342.
- Sainburg RL, Poizner H. & Ghez C. (1993). Loss of proprioception produces deficits in interjoint coordination. Journal of Neurophysiology 70 (5): 2136–47. PMID 8294975.
- Ghez C., Gordon J. & Ghilardi M.F. (1995). Impairments of reaching movements in patients without proprioception. II. Effects of visual information on accuracy. Journal of Neurophysiology 73 (1): 361–72. PMID 7714578.
- Favilla, M.; Hening, W.; Ghez, C. (1989). Trajectory control in targeted force impulses. Experimental Brain Research 75 (2). ISSN 0014-4819. doi:10.1007/BF00247934.
- Morasso Pietro G. (1981). Spatial control of arm movements. Experimental Brain Research 42 (2). ISSN 0014-4819. doi:10.1007/BF00236911.
- Knierim James. Ph.D. "Section III. Chapter 3. Motor Cortex" Архівовано 10 березня 2016 у Wayback Machine. Neuroscience Online: An Electronic Textbook for the Neurosciences. Department of Neurobiology and Anatomy — The University of Texas Medical School at Houston
- Kass R. E., Ventura V. & Brown E.N. (2005). Statistical Issues in the Analysis of Neuronal Data. Journal of Neurophysiology 94 (1): 8–25. ISSN 0022-3077. doi:10.1152/jn.00648.2004.
- Paninski Liam (2013). » Statistical analysis of neural data: Regression approaches for modeling neural responses and stimulus decoding " (Lecture notes)
- Paninski, Liam (2004). Maximum likelihood estimation of cascade point-process neural encoding models. Network: Computation in Neural Systems 15 (4): 243–262. ISSN 0954-898X. doi:10.1088/0954-898X_15_4_002.
- Kettner R.E., Schwartz A.B. & Georgopoulos A.P. (1988). Primate motor cortex and free arm movements to visual targets in three-dimensional space. III. Positional gradients and population coding of movement direction from various movement origins. The Journal of Neuroscience 8 (8): 2938–47. PMID 3411363.
- Schwartz Andrew B. (1992). Motor cortical activity during drawing movements: single-unit activity during sinusoid tracing. Journal of Neurophysiology 68 (2): 528–41. PMID 1527573.
- Schwartz AB & Moran DW (1999). Motor cortical activity during drawing movements: population representation during lemniscate tracing. J. Neurophysiol. 82 (5): 2705–18. PMID 10561439.
- Sanger T.D. (1996). Probability density estimation for the interpretation of neural population codes. Journal of Neurophysiology 76 (4): 2790–3. PMID 8899646.
- Maynard EM, Hatsopoulos NG, Ojakangas CL, Acuna BD, Sanes JN, Normann RA & Donoghue JP (1999). Neuronal interactions improve cortical population coding of movement direction. The Journal of Neuroscience 19 (18): 8083–93. PMID 10479708.
- Oram MW, Hatsopoulos NG, Richmond BJ & Donoghue JP (2001). Excess synchrony in motor cortical neurons provides redundant direction information with that from coarse temporal measures. Journal of Neurophysiology 86 (4): 1700–16. PMID 11600633.
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD & Donoghue JP (2006). Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature 442 (7099): 164–171. ISSN 0028-0836. doi:10.1038/nature04970.
- Truccolo W., Friehs G. M., Donoghue J. P. & Hochberg L. R. (2008). Primary Motor Cortex Tuning to Intended Movement Kinematics in Humans with Tetraplegia. Journal of Neuroscience 28 (5): 1163–1178. ISSN 0270-6474. doi:10.1523/JNEUROSCI.4415-07.2008.
- Truccolo W., Hochberg L.R. & Donoghue J.P. (2009). Collective dynamics in human and monkey sensorimotor cortex: predicting single neuron spikes. Nature Neuroscience 13 (1): 105–111. ISSN 1097-6256. doi:10.1038/nn.2455.
- Philip B.A., Rao N. & Donoghue J.P. (2012). Simultaneous reconstruction of continuous hand movements from primary motor and posterior parietal cortex. Experimental Brain Research 225 (3): 361–375. ISSN 0014-4819. doi:10.1007/s00221-012-3377-0.
- Reimer J. & Hatsopoulos N. G. (2010). Periodicity and Evoked Responses in Motor Cortex. Journal of Neuroscience 30 (34): 11506–11515. ISSN 0270-6474. doi:10.1523/JNEUROSCI.5947-09.2010.
- Wang W., Chan S. S., Heldman D. A. & Moran D. W. (2007). Motor Cortical Representation of Position and Velocity During Reaching. Journal of Neurophysiology 97 (6): 4258–4270. ISSN 0022-3077. doi:10.1152/jn.01180.2006.
- Wang, W.; Chan, S. S.; Heldman, D. A.; Moran, D. W. (2010). Motor Cortical Representation of Hand Translation and Rotation during Reaching. Journal of Neuroscience 30 (3): 958–962. ISSN 0270-6474. doi:10.1523/JNEUROSCI.3742-09.2010.
- Paninski, Liam (2003). Convergence properties of three spike-triggered analysis techniques. Network: Computation in Neural Systems 14 (3): 437–464. ISSN 0954-898X. doi:10.1088/0954-898X_14_3_304.
- Simoncelli, E. P., Paninski, L., Pillow, J. & Swartz, O. (2004). Characterization of Neural Responses with Stochastic Stimuli. У Gazzaniga M. The Cognitive Neurosciences 3rd edn. MIT Press. с. 327–338.
- Paninski Liam (2007). "Statistical analysis of neural data. Classification-based approaches: spike-triggered averaging, spike-triggered covariance, and the linear-nonlinear cascade model "(Lecture notes)
- Lee D, Port NL, Kruse W & Georgopoulos AP (1998). Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. The Journal of Neuroscience 18 (3): 1161–70. PMID 9437036.
- Leyton A.S.F. and Sherrington C.S. (1917). Observation on the excitable cortex of the chimpanzee, orang-utan, and gorilla. Quarterly Journal of Experimental Physiology 11 (2): 135–222. ISSN 03702901. doi:10.1113/expphysiol.1917.sp000240.
- Lemon R.N. (2008). An enduring map of the motor cortex. Experimental Physiology 93 (7): 798–802. ISSN 09580670. doi:10.1113/expphysiol.2007.039081.
- Graziano, Michael S.A; Taylor, Charlotte S.R; Moore, Tirin (2002). Complex Movements Evoked by Microstimulation of Precentral Cortex. Neuron 34 (5): 841–851. ISSN 08966273. doi:10.1016/S0896-6273(02)00698-0.
- Graziano, M. S. A. (2005). Arm Movements Evoked by Electrical Stimulation in the Motor Cortex of Monkeys. Journal of Neurophysiology 94 (6): 4209–4223. ISSN 0022-3077. doi:10.1152/jn.01303.2004.
- Graziano, Michael S.A. (2016). Ethological Action Maps: A Paradigm Shift for the Motor Cortex. Trends in Cognitive Sciences 20 (2): 121–132. ISSN 13646613. doi:10.1016/j.tics.2015.10.008.
- Mason Carolyn R., Johnson Michael T. V., Fu Qing-Gong, Gomez Jose E. and Ebner Timothy J. (1998). Temporal profile of the directional tuning of the discharge of dorsal premotor cortical cells. NeuroReport 9 (6): 989–995. ISSN 0959-4965. doi:10.1097/00001756-199804200-00007.
- Sergio LE and Kalaska JF (1998). Changes in the temporal pattern of primary motor cortex activity in a directional isometric force versus limb movement task. Journal of Neurophysiology 80 (3): 1577–83. PMID 9744964.
- Hocherman, S.; Wise, S.P. (1991). Effects of hand movement path on motor cortical activity in awake, behaving rhesus monkeys. Experimental Brain Research 83 (2). ISSN 0014-4819. doi:10.1007/BF00231153.
- Hatsopoulos, N. G.; Xu, Q.; Amit, Y. (2007). Encoding of Movement Fragments in the Motor Cortex. Journal of Neuroscience 27 (19): 5105–5114. ISSN 0270-6474. doi:10.1523/JNEUROSCI.3570-06.2007.
- Scott Stephen H. (2000). Population vectors and motor cortex: neural coding or epiphenomenon?. Nature Neuroscience 3 (4): 307–308. ISSN 10976256. doi:10.1038/73859.
- Georgopoulos Apostolos P. and Ashe James (2000). One motor cortex, two different views. Nature Neuroscience 3 (10): 963–963. ISSN 10976256. doi:10.1038/79882.
- Moran Daniel W. and Schwartz Andrew B. (2000). One motor cortex, two different views. Nature Neuroscience 3 (10): 963–963. ISSN 10976256. doi:10.1038/79880.
- Scott Stephen H. (2000). Reply to 'One motor cortex, two different views'. Nature Neuroscience 3 (10): 964–965. ISSN 10976256. doi:10.1038/79888.
- Todorov Emanuel (2000). Reply to 'One motor cortex, two different views'. Nature Neuroscience 3 (10): 963–964. ISSN 10976256. doi:10.1038/79884.
- Shenoy Krishna V., Sahani Maneesh and Churchland Mark M. (2013). Cortical Control of Arm Movements: A Dynamical Systems Perspective. Annual Review of Neuroscience 36 (1): 337–359. ISSN 0147-006X. doi:10.1146/annurev-neuro-062111-150509.
- Soechting J F and Flanders M (1992). Moving in Three-Dimensional Space: Frames of Reference, Vectors, and Coordinate Systems. Annual Review of Neuroscience 15 (1): 167–191. ISSN 0147-006X. doi:10.1146/annurev.ne.15.030192.001123.
- Georgopoulos Apostolos P. and Carpenter Adam F. (2015). Coding of movements in the motor cortex. Current Opinion in Neurobiology 33: 34–39. ISSN 09594388. doi:10.1016/j.conb.2015.01.012.
- Amirikian Bagrat and Georgopulos Apostolos P (2000). Directional tuning profiles of motor cortical cells. Neuroscience Research 36 (1): 73–79. ISSN 01680102. doi:10.1016/S0168-0102(99)00112-1.
- Georgopoulos Apostolos P. (2014). Cell directional spread determines accuracy, precision, and length of the neuronal population vector. Experimental Brain Research 232 (7): 2391–2405. ISSN 0014-4819. doi:10.1007/s00221-014-3936-7.
Посилання
- Сукупність інтерактивних демонстрацій моторного керування рухами. Моделі вектора популяції, кодування нейронами м'язової активації, сили, швидкості, положення тощо.