Обернений гамма розподіл
У теорії ймовірностей і статистиці обернений гамма розподіл — це двопараметрічна сім’я неперервних розподілів ймовірностей на додатній дійсній півосі, що є розподілом оберненої до змінної, що має гамма-розподіл. Мабуть найбільше обернений гамма-розподіл використовується в баєсівській статистиці, де такий розподіл виникає як граничний апостеріорний розподіл для невідомої дисперсії нормального розподілу, якщо використовується неінформативний апріор, і як аналітично виражений спряжений апріор у випадку інформативного апріорного розподілу.
| Обернений гамма | |
|---|---|
|
Щільність розподілу 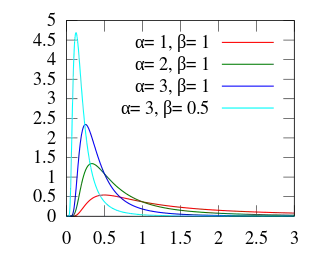 | |
|
Функція розподілу ймовірностей  | |
| Параметри |
форма (дійсне) масштаб (дійсне) |
| Носій функції | |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | для |
| Мода | |
| Дисперсія | для |
| Коефіцієнт асиметрії | для |
| Коефіцієнт ексцесу | для |
| Ентропія |
(див. дигамма-функція) |
| Характеристична функція | |
Однак серед баєсівців прийнято розглядати альтернативну параметризацію нормального розподілу з точки зору точності, що визначається як зворотна величина дисперсії, що дозволяє використовувати гамма-розподіл безпосередньо як спряжений апріор. Інші баєсівці вважають за краще параметрізувати зворотний гамма-розподіл інакше, як масштабований обернений розподіл хі-квадрат .
Характеристика
Функція щільності
Функція щільності ймовірності оберненого гамма-розподілу визначається на носії
з параметром форми і параметром масштабу [1]. Тут позначає гамма-функцію.
На відміну від гамма-розподілу, який містить дещо подібний експоненціальний член, є параметром масштабу, оскільки функція розподілу задовольняє умову:
Функція розподілу
Функція розподілу є регуляризованою гамма-функцією
де чисельник — це верхня неповна гамма-функція, а знаменник — гамма-функція . Багато математичних пакетів дозволяють безпосередньо обчислити , регуляризовану гамма-функцію.
Характеристична функція
у виразі характеристичної функції є модифікованою функціє. Бесселя 2-го роду.
Властивості
Для і ,
і
Інформаційна ентропія обислюється наступним чином
де — дигамма функція.
Розбіжність Кульбака-Лейблера оберненої-гамми ( α p, β p ) від оберненої-гамми ( α q, β q ) така сама, як і KL-розбіжність гамма ( α p, β p ) від гамма ( α q, β q ):
де є щільностями обернених гамма-розподілів та є щільностями гамма-розподілів, має Гамма( α p, β p ) розподіл.
Пов'язані розподіли
- Якщо тоді
- Якщо тоді (обернений хі-квадрат розподіл)
- Якщо тоді (масштабований обернений хі-квадрат <a href="./Обернений розподіл хі-квадрат" rel="mw:WikiLink" data-linkid="164" data-cx="{&quot;adapted&quot;:false,&quot;sourceTitle&quot;:{&quot;title&quot;:&quot;Inverse-chi-squared distribution&quot;,&quot;thumbnail&quot;:{&quot;source&quot;:&quot;https://upload.wikimedia.org/wikipedia/en/thumb/5/5a/Inverse_chi_squared_density.png/62px-Inverse_chi_squared_density.png&quot;,&quot;width&quot;:62,&quot;height&quot;:80},&quot;description&quot;:&quot;Probability distribution&quot;,&quot;pageprops&quot;:{&quot;wikibase_item&quot;:&quot;Q3258519&quot;},&quot;pagelanguage&quot;:&quot;en&quot;},&quot;targetFrom&quot;:&quot;mt&quot;}" class="cx-link" id="mwhQ" title="Обернений розподіл хі-квадрат">розподіл</a>)
- Якщо тоді (розподіл Леві)
- Якщо тоді (експоненційний розподіл)
- Якщо ( Гамма-розподіл з параметром темпу ) тоді (Деталі див. виведення в наступному абзаці)
- Зверніть увагу, що якщо (Гамма-розподіл з параметром масштабу ) тоді
- Обернений гамма-розподіл є окремим випадком розподілу Пірсона 5го типу
- Багатовимірним узагальненням оберненого гамма-розподілу є обернений розподіл Вішарта.
- Про розподіл суми незалежних обернених гамма-змінних див. Witkovsky (2001)
Виведення з гамма-розподілу
Нехай , і нагадаємо, що щільність гамма-розподілу
- , .
Враховуючи, що – параметр темпу змін в гамма-розподілі.
Визначимо перетворення . Далі щільність записується
Зауважте, що – параметр масштабу для оберненого гамма-розподілу.
Поява
- Розподіл часу відліку вінерівського процесу [3]
Див. також
- Гамма-розподіл
- Обернений розподіл хі-квадрат
- Нормальний розподіл
Примітки
- InverseGammaDistribution—Wolfram Language Documentation. reference.wolfram.com. Процитовано 9 квітня 2018.
- John D. Cook (3 жовтня 2008). InverseGammaDistribution. Процитовано 3 грудня 2018.
- Ludkovski, Mike (2007). Math 526: Brownian Motion Notes. UC Santa Barbara. с. 5–6.
Джерела
- Hoff, P. (2009). "A first course in bayesian statistical methods". Springer.
- Witkovsky, V. (2001). Computing the Distribution of a Linear Combination of Inverted Gamma Variables. Kybernetika 37 (1): 79–90. MR 1825758. Zbl 1263.62022.