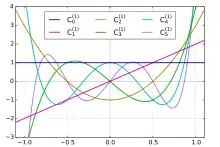
Поліноми Ґеґенбауера

Графіки поліномів Ґеґенбауера при ${\displaystyle \alpha =1}$

Перші шість поліномів Ґеґенбауера:[2]

${\displaystyle {\begin{aligned}C_{0}^{\alpha }(z)&=1,\\C_{1}^{\alpha }(z)&=2\alpha z,\\C_{2}^{\alpha }(z)&=2\alpha (1+\alpha )z^{2}-\alpha ,\\C_{3}^{\alpha }(z)&={\tfrac {4}{3}}\alpha (1+\alpha )(2+\alpha )z^{3}-2\alpha (1+\alpha )z,\\C_{4}^{\alpha }(z)&={\tfrac {2}{3}}\alpha (1+\alpha )(2+\alpha )(3+\alpha )z^{4}-2\alpha (1+\alpha )(2+\alpha )z^{2}+{\tfrac {1}{2}}\alpha (1+\alpha ),\\C_{5}^{\alpha }(z)&={\tfrac {4}{15}}\alpha (1+\alpha )(2+\alpha )(3+\alpha )(4+\alpha )z^{5}-{\tfrac {4}{3}}\alpha (1+\alpha )(2+\alpha )(3+\alpha )z^{3}+\alpha (1+\alpha )(2+\alpha )z.\end{aligned}}}$

Мають місце такі співвідношення:

• при ${\displaystyle x=0}$

${\displaystyle C_{2n}^{(\alpha )}(0)={\frac {(-1)^{n}(\alpha )_{n}}{(n)!}}}$,       ${\displaystyle C_{2n-1}^{(\alpha )}(0)=0;}$

• при ${\displaystyle x=1}$

${\displaystyle C_{n}^{(\alpha )}(1)={\frac {(2\alpha )_{n}}{n!}};}$

• при ${\displaystyle x=-1}$

${\displaystyle C_{n}^{(\alpha )}(-1)=(-1)^{n}{\frac {(2\alpha )_{n}}{n!}}.}$

• Функція ${\displaystyle C_{n}^{(\alpha )}(z)}$ є поліномом степеня ${\displaystyle n}$ відносно ${\displaystyle z}$ та ${\displaystyle \alpha }$ і визначена для довільних ${\displaystyle z,\alpha \in \mathbb {C} }$.

• Як і всі ортогональні поліноми функція ${\displaystyle C_{n}^{(\alpha )}(z)}$, ${\displaystyle \alpha >-{\tfrac {1}{2}}}$, має тільки прості нулі, які всі лежать на відрізку ${\displaystyle [-1,1]}$. Нулі розташовані симетрично відносно початку координат. Нулі поліномів ${\displaystyle C_{n}^{(\alpha )}(z)}$ та ${\displaystyle C_{n+1}^{(\alpha )}(z)}$ чергуються.

Позначимо через ${\displaystyle x_{m},m=1,\ldots ,n,}$ нулі многочлена ${\displaystyle C_{n}^{(\alpha )}(z)}$ розташовані у порядку спадання:

${\displaystyle C_{n}^{(\alpha )}(x_{m})=0,\qquad -1<x_{n}<x_{n-1}<\cdots <x_{1}<1,}$

Нулі розташовані симетрично ${\displaystyle x_{m}=-x_{n-m},m=1,\ldots ,[n/2],}$. Для нулів на інтеравалі [0,1] введемо позначення

${\displaystyle x_{m}=\cos(\theta _{m}),\quad \theta _{1}<\cdots <\theta _{m},\quad m=1,\ldots ,[n/2].}$

Тоді мають місце оцінки:[3]

${\displaystyle \left(m-{\frac {1}{2}}\right){\frac {\pi }{n}}\leq \theta _{m}\leq {\frac {m\pi }{n+1}},\quad m=1,\ldots ,[n/2].}$

• Поліном ${\displaystyle C_{n}^{(\alpha )}(z)}$ містить члени лише тієї ж парності, що й саме число ${\displaystyle n}$:

${\displaystyle C_{n}^{(\alpha )}(-z)=(-1)^{n}C_{n}^{(\alpha )}(z),\quad n=0,1,2,\ldots .}$

• Поліноми Лежандра ${\displaystyle P_{n}(z)}$ є частковим випадком поліномів Ґеґенбауера при ${\displaystyle \alpha ={\tfrac {1}{2}}}$:

${\displaystyle P_{n}(z)=C_{n}^{(1/2)}(z).}$

У загальному випадку поліноми Ґеґенбауера півцілого верхнього індексу можна виразити через поліноми Лежандра:

${\displaystyle C_{n}^{\left(m+{\tfrac {1}{2}}\right)}(z)=\sum _{k_{1}=0}^{n}\cdots \sum _{k_{2m+1}=0}^{n}\delta _{n,l}\prod _{j=1}^{2m+1}P_{k_{j}}(z),\quad l=\sum _{j=1}^{2m+1}k_{j},}$

де ${\displaystyle \delta _{n,l}}$ — символ Кронекера, або через похідну від полінома Лежандра:

${\displaystyle C_{n}^{\left(m+{\tfrac {1}{2}}\right)}(z)={\frac {2^{m}m!}{(2m)!}}{\frac {d^{m}}{dz^{m}}}P_{n+m}(z),\quad m=0,1,2,\ldots .}$

• Приєднана функція Лежандра першого роду також може бути виражена через поліноми Ґеґенбауера:

${\displaystyle P_{n}^{m}(z)={\frac {(-1)^{m}}{\sqrt {\pi }}}\Gamma \left(m+{\tfrac {1}{2}}\right)2^{m}(1-z^{2})^{\tfrac {m}{2}}C_{n-m}^{\left(m+{\tfrac {1}{2}}\right)}(z).}$

• Поліноми Чебишева першого роду ${\displaystyle T_{n}(z)}$ є частковим випадком поліномів Ґеґенбауера при ${\displaystyle \alpha \rightarrow 0}$:

${\displaystyle T_{n}(z)={\frac {n}{2}}\lim _{\alpha \rightarrow 0}\left({\frac {1}{\alpha }}C_{n}^{(\alpha )}(z)\right).}$

Це співвідношення беруть за означення полінома Ґеґенбауера індекса ${\displaystyle \alpha =0}$, тобто ${\displaystyle C_{n}^{(0)}(z):=T_{n}(z)}$.

• Поліноми Чебишева другого роду ${\displaystyle U_{n}(z)}$ є частковим випадком поліномів Ґеґенбауера при ${\displaystyle \alpha =1}$

${\displaystyle U_{n}(z)=C_{n}^{(1)}(z).}$

У загальному випадку поліноми Ґеґенбауера цілого верхнього індексу можна виразити через поліноми Чебишева:

${\displaystyle C_{n}^{(m)}(z)=\sum _{k_{1}=0}^{n}\cdots \sum _{k_{m}=0}^{n}\delta _{n,l}\prod _{j=1}^{m}U_{k_{j}}(z),\quad l=\sum _{j=1}^{m}k_{j},\quad m=1,2,\ldots ,}$

де ${\displaystyle \delta _{n,l}}$ — символ Кронекера, або за допомогою операції диференціювання:

${\displaystyle C_{n}^{(m)}(z)={\frac {2^{-m+1}m!}{(m-1)!(n+m)}}{\frac {d^{m}}{dz^{m}}}T_{n+m}(z),\quad m=1,2,\ldots .}$

• Поліноми Ерміта також можуть бути виражені як граничний випадок поліномів ${\displaystyle C_{n}^{(\alpha )}(z)}$:

${\displaystyle H_{n}(z)={\frac {n!}{2}}\lim _{\alpha \rightarrow 0}\left(\alpha ^{-{\tfrac {n}{2}}}C_{n}^{(\alpha )}\left({\frac {z}{\sqrt {\alpha }}}\right)\right).}$

• Поліноми Ґеґенбауера можна виразити через скінченний гіпергеометричний ряд:[4]

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {(2\alpha )_{n}}{n!}}\,_{2}F_{1}\left(-n,2\alpha +n;\alpha +{\tfrac {1}{2}};{\tfrac {1}{2}}(1-z)\right),\qquad \alpha +{\tfrac {1}{2}}\neq -n,n\in \mathbb {N} ,}$

${\displaystyle C_{2m}^{(\alpha )}(z)=(-1)^{m}{\frac {(\alpha )_{m}}{m!}}\,_{2}F_{1}\left(-m,\alpha +m;{\tfrac {1}{2}};x^{2}\right),\qquad C_{2m+1}^{(\alpha )}(z)=(-1)^{m}{\frac {(\alpha )_{m+1}}{m!}}\,_{2}F_{1}\left(-m,\alpha +m+1;{\tfrac {3}{2}};x^{2}\right).}$

Це співвідношення дозволяє розширити означення функції ${\displaystyle C_{n}^{(\alpha )}(z)}$ на випадок довільного дійсного (комплесного) значення індексу ${\displaystyle n}$. Так означена функція ${\displaystyle C_{\beta }^{(\alpha )}(z)}$ називається функцією Ґеґенбауера і у випадку натурального ${\displaystyle \beta }$ збігається з поліномом Ґеґенбауера.

• Поліноми Ґеґенбауера є частковим випадком поліномів Якобі ${\displaystyle P_{n}^{(\mu ,\nu )}(z)}$ при ${\displaystyle \mu =\nu =\alpha -{\tfrac {1}{2}}}$:

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {(2\alpha )_{n}}{(\alpha +{\frac {1}{2}})_{n}}}P_{n}^{(\alpha -1/2,\;\alpha -1/2)}(z),}$

де ${\displaystyle (\cdot )_{n}}$ — символ Похгаммера.

Твірна функція поліномів Ґеґенбауера [5]:

${\displaystyle {\frac {1}{(1-2zt+t^{2})^{\alpha }}}=\sum _{n=0}^{\infty }C_{n}^{(\alpha )}(z)t^{n}.}$

Вони можуть бути виражені за допомогою формули Родріга

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {(-2)^{n}}{n!}}{\frac {\Gamma (n+\alpha )\Gamma (n+2\alpha )}{\Gamma (\alpha )\Gamma (2n+2\alpha )}}(1-z^{2})^{-\alpha +1/2}{\frac {{\rm {d}}^{n}}{{\rm {d}}z^{n}}}\left[(1-z^{2})^{n+\alpha -1/2}\right].}$

Для поліномів Ґеґенбауера виконується рекурентне співвідношення по індексу ${\displaystyle n}$, яке можна застосовувати для знаходження поліномів при ${\displaystyle n\geq 2}$:

${\displaystyle C_{0}^{(\alpha )}(z)=1,\quad C_{1}^{(\alpha )}(z)=2\alpha z,\quad C_{n+1}^{(\alpha )}(z)={\frac {1}{n+1}}[2z(n+\alpha )C_{n}^{(\alpha )}(z)-(n+2\alpha -1)C_{n-1}^{(\alpha )}(z)].}$

Рекурентне співвідношення по індексу ${\displaystyle \alpha }$:

${\displaystyle C_{n}^{(\alpha +1)}(z)={\frac {2\alpha z^{2}+2n(z^{2}-1)+4\alpha -1}{2\alpha (z^{2}-1)}}C_{n}^{(\alpha )}(z)+{\frac {(n+2\alpha -2)(n+2\alpha -1)}{4\alpha (\alpha -1)(z^{2}-1)}}C_{n}^{(\alpha -1)}(z).}$

Інші формули:

${\displaystyle C_{n}^{(\alpha )}(z)=zC_{n}^{(\alpha )}(z)+{\frac {n+2\alpha -2}{2\alpha -2}}C_{n}^{(\alpha -1)}(z),}$

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {(n+1)z}{n+2\alpha }}C_{n+1}^{(\alpha )}(z)-{\frac {2\alpha (z^{2}-1)}{n+2\alpha }}C_{n}^{(\alpha +1)}(z),}$

${\displaystyle n(n+2\alpha )C_{n}^{(\alpha )}(z)-2\alpha (2\alpha +1)zC_{n-1}^{(\alpha +1)}(z)-4\alpha (\alpha +1)(z^{2}-1)C_{n-2}^{(\alpha +2)}(z)=0.}$

Похідна полінома Ґеґенбауера виражається через поліном зі зміщеним індексом

${\displaystyle {\frac {d}{dz}}C_{n}^{(\alpha )}(z)=2\alpha C_{n-1}^{(\alpha +1)}(z)}$

або у загальному випадку

${\displaystyle {\frac {d^{m}}{dz^{m}}}C_{n}^{(\alpha )}(z)=2^{m}(\alpha )_{m}C_{n-m}^{(\alpha +m)}(z).}$

Похідна від добутку на вагову функцію

${\displaystyle {\frac {d}{dz}}\left((1-z^{2})^{\alpha -{\tfrac {1}{2}}}C_{n}^{(\alpha )}(z)\right)=-{\frac {(n+1)(n+2\alpha +1)}{2(\alpha -1)}}(1-z^{2})^{\alpha -{\tfrac {3}{2}}}C_{n+1}^{(\alpha -1)}(z).}$

Похідна полінома Ґеґенбауера по параметру ${\displaystyle \alpha }$ також може бути обчислена через поліноми за наступною формулою:[6]

${\displaystyle {\frac {d}{d\alpha }}C_{n}^{(\alpha )}(z)=\sum _{k=0}^{n-1}\left({\frac {2(1+(-1)^{n-k})(k+\alpha )}{(n+k+2\alpha )(n-k)}}C_{k}^{(\alpha )}(z)+\left({\frac {2(k+1)}{(k+2\alpha )(2k+2\alpha +1)}}+{\frac {2}{(n+k+2\alpha )}}\right)C_{n}^{(\alpha )}(z)\right).}$

Зауваження. Всі співвідношення цього розділу справедливі за умови ${\displaystyle \alpha >-{\tfrac {1}{2}}}$, ${\displaystyle -1\leq z\leq 1}$.

Для заданого ${\displaystyle \alpha >-{\tfrac {1}{2}}}$ поліноми Ґеґенбауера ортогональні на відрізку [−1,1] с вагою ${\displaystyle (1-z^{2})^{\alpha -1/2}}$, тобто (при ${\displaystyle n\neq m}$)[8],

${\displaystyle \int _{-1}^{1}C_{n}^{(\alpha )}(z)C_{m}^{(\alpha )}(z)(1-z^{2})^{\alpha -1/2}\,{\rm {d}}z=0,}$

причому виконується умова нормування [8]

${\displaystyle \|C_{n}^{(\alpha )}(z)\|^{2}=\int _{-1}^{1}\left[C_{n}^{(\alpha )}(z)\right]^{2}(1-z^{2})^{\alpha -1/2}\,{\rm {d}}z={\frac {2^{1-2\alpha }\pi \Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}.}$

Як наслідок, функції

${\displaystyle \psi _{n}^{\alpha }(z):={\frac {2^{{\tfrac {1}{2}}-\alpha }{\sqrt {\pi \Gamma (n+2\alpha )}}}{\Gamma (\alpha ){\sqrt {n!(n+\alpha )}}}}(1-z^{2})^{\frac {1-2\alpha }{4}}C_{n}^{(\alpha )}(z),\quad n=0,1,2,\ldots ,}$

утворюють ортонормований базис у просторі ${\displaystyle L^{2}[-1,1]}$. Довільна функція ${\displaystyle f(z)\in L^{2}[-1,1]}$ може бути розвинена в узагальнений ряд Фур'є по набору функцій ${\displaystyle \{\psi _{n}^{\alpha }(z)\}_{n=0}^{\infty }}$:

${\displaystyle f(z)=\sum _{k=0}^{\infty }f_{k}\psi _{k}^{\alpha }(z),\quad f_{k}=\int _{-1}^{1}f(z)\psi _{k}^{\alpha }(z)dz.}$

Також розвинення можна будувати безпосередньо по многочленах Ґеґенбауера у ваговому просторі Лебега ${\displaystyle L_{w}^{2}[-1,1]}$:[9]

${\displaystyle L_{w}^{2}[-1,1]:=\left\{f(z):\int _{-1}^{1}f^{2}(z)w(z)dz<\infty \right\},\quad w(z)=(1-z^{2})^{\alpha -1/2},}$

за формулами:

${\displaystyle f(z)=\sum _{k=0}^{\infty }f_{k}C_{k}^{(\alpha )}(z),\quad f_{k}={\tfrac {1}{N_{k}}}\int _{-1}^{1}f(z)C_{k}^{(\alpha )}(z)dz,\quad N_{k}={\frac {2^{1-2\alpha }\pi \Gamma (k+2\alpha )}{k!(k+\alpha )[\Gamma (\alpha )]^{2}}}.}$

Поліноми Ґеґенбауера ${\displaystyle C_{n}^{(\alpha )}(z)}$ можна записати у вигляді суми по степенях ${\displaystyle z}$ або ${\displaystyle \alpha }$ за відповідними формулами:

${\displaystyle C_{n}^{(\alpha )}(z)=\sum _{k=0}^{\lfloor n/2\rfloor }{\frac {(-1)^{k}(\alpha )_{n-k}}{k!(n-2k)!}}(2z)^{n-2k},}$

${\displaystyle C_{n}^{(\alpha )}(z)=\sum _{k=1}^{n}\sum _{j=0}^{\lfloor n/2\rfloor }{\frac {(-1)^{k+n}(2z)^{n-2j}s(n-j,k)}{j!(n-2j)!}}\alpha ^{k},}$

де ${\displaystyle s(n-j,k)}$ — числа Стірлінга першого роду.

Розвиненням в ряд Тейлора в околі довільної точки ${\displaystyle z=z_{0}}$ буде скінчення сума:

${\displaystyle C_{n}^{(\alpha )}(z)=\sum _{k=0}^{n}{\frac {2^{k}(\alpha )_{k}}{k!}}C_{n-k}^{(\alpha +k)}(z_{0})(z-z_{0})^{k}.}$

Поліноми Ґеґенбауера допускають інтегральне представлення:

через інтеграл по дійсній змінній:

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {2^{1-2\alpha }\pi \Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}\int _{0}^{\pi }(z+\cos t\cdot {\sqrt {z^{2}-1}})^{n}(\sin t)^{2\alpha -1}dt,}$

через контурний інтеграл:

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {du}{u^{n+1}(1-2zu+u^{2})^{\alpha }}},}$

де ${\displaystyle \gamma }$ — довільний контур в комплексній області, що містить одиничний круг.

Ряд інших інтегральних тотожностей:

${\displaystyle \int C_{n}^{(\alpha )}(z)dz={\frac {1}{2(\alpha -1)}}C_{n+1}^{(\alpha -1)}(z)+C,}$

${\displaystyle \int C_{n}^{({\tfrac {3}{2}})}(z)dz=P_{n+1}(z)+C,\quad \int C_{n}^{(2)}(z)dz={\tfrac {1}{2}}U_{n+1}(z)+C,}$

${\displaystyle \int (1-z^{2})^{\alpha -{\tfrac {1}{2}}}C_{n}^{(\alpha )}(z)dz=-{\frac {2\alpha (1-z^{2})^{\alpha +{\tfrac {1}{2}}}}{n(n+2\alpha )}}C_{n-1}^{(\alpha +1)}(z)+C.}$

Наведені формули характеризують поведінку поліномів Ґеґенбауера в околі різних значень параметра ${\displaystyle \alpha }$ та змінної ${\displaystyle z}$:[6]

${\displaystyle C_{n}^{(\alpha )}(z)\approx {\frac {2^{n}{\sqrt {\pi }}\Gamma (\alpha +{\tfrac {1}{2}})}{\Gamma (\alpha )\Gamma ({\tfrac {1-n}{2}})n!}}(1+O(z));\qquad C_{n}^{(\alpha )}(z)\approx {\frac {\Gamma (2\alpha +n)}{\Gamma (2\alpha )n!}}(1+O(z-1)),\quad -\alpha -{\tfrac {1}{2}}\neq \mathbb {N}$ ;}

${\displaystyle C_{n}^{(\alpha )}(z)\approx {\frac {(-1)^{n}(2\alpha )_{n}}{n!}}(1+O(z+1));\qquad C_{n}^{(\alpha )}(z)\approx {\frac {2^{n}z^{n}(\alpha )_{n}}{n!}}\left(1+O\left({\frac {1}{z^{2}}}\right)\right);}$

${\displaystyle C_{n}^{(\alpha )}(z)\approx C_{n}^{(0)}(z)\alpha (1+O(\alpha )),\quad n>0;\qquad C_{n}^{(\alpha )}(z)\approx {\frac {(2z)^{n}\alpha ^{n}}{n!}}\left(1+O\left({\frac {1}{\alpha }}\right)\right).}$

Справедливі такі оцінки:[10]

${\displaystyle \max _{-1\leq z\leq 1}|C_{n}^{(\alpha )}(z)|=C_{n}^{(\alpha )}(1)={\frac {(2\alpha )_{n}}{n!}},\quad \alpha >0}$

${\displaystyle \max _{-1\leq z\leq 1}|C_{2m}^{(\alpha )}(z)|=|C_{2m}^{(\alpha )}(0)|=\left|{\frac {(\alpha )_{m}}{m!}}\right|,\quad -m<\alpha <0,\quad \alpha \neq \mathbb {Z} ,}$

${\displaystyle \max _{-1\leq z\leq 1}|C_{2m+1}^{(\alpha )}(z)|<{\frac {2|(\alpha )_{m+1}|}{m!{\sqrt {(2m+1)(2m+2\alpha +1)}}}},\quad -m-{\tfrac {1}{2}}<\alpha <0,\quad \alpha \neq \mathbb {Z} ,}$

${\displaystyle (1-z^{2})^{\alpha }|C_{n}^{(\alpha )}(z)|<\left({\frac {n}{2}}\right)^{\alpha }{\frac {1}{\Gamma (\alpha )}},\quad 0<\alpha <1,\quad z\in [-1,1].}$

При ${\displaystyle z\geq -1,\,\alpha \geq 1/4}$ справедлива наступна нерівність:

${\displaystyle \sum _{j=0}^{n}{\frac {C_{j}^{(\alpha )}(z)}{2\alpha +j-1 \choose j}}\geq 0,\qquad {2\alpha +j-1 \choose j}={\frac {(2\alpha +j-1)(2\alpha +j-2)(2\alpha +j-3)\cdots (2\alpha )}{j(j-1)(j-2)\cdots 1}}.}$

Поліном Ґеґенбауера від косинуса полярного кута ${\displaystyle \theta }$ може бути представлений у вигляді суми[11]

${\displaystyle C_{n}^{(\alpha )}(\cos \theta )=\sum _{k=0}^{n}{\frac {(\alpha )_{k}(\alpha )_{n-k}}{k!(n-k)!}}\cos((n-2k)\theta ),}$

або через інтеграл від дійсного параметра:

${\displaystyle C_{n}^{(\alpha )}(\cos \theta )={\frac {2^{\alpha }\Gamma (\alpha +{\tfrac {1}{2}})(2\alpha )_{n}}{n!\Gamma (\alpha ){\sqrt {pi}}}}\int _{0}^{\theta }{\frac {\cos((n+\alpha )\phi )}{(\cos \phi -\cos \theta )^{1-\alpha }}}d\phi .}$

Зауваження. Наведені вище формули справедливі для косинуса взагалі, без прив'язки до сферичної системи координат.

При повороті точки заданої в сферичній системі координатами ${\displaystyle (r,\theta ,\varphi )}$ на кут нутації ${\displaystyle \beta }$ новий кут ${\displaystyle \theta ^{\prime }}$ визначається рівністю

${\displaystyle \cos \theta ^{\prime }=\cos \theta \cos \beta +\sin \theta \sin \beta \cos \varphi .}$

Справедлива формула додавання:

${\displaystyle C_{n}^{(\alpha )}(\cos \theta ^{\prime })=\sum _{k=0}^{n}{\frac {(\alpha )_{k}(n-k)!}{(\alpha +{\tfrac {1}{2}})_{k}(2k+2\alpha )_{n-k}}}\sin ^{k}\theta \,\sin ^{k}\beta \,C_{n-k}^{(\alpha +k)}(\cos \theta )\,C_{n-k}^{(\alpha +k)}(\cos \beta )\,C_{k}^{(\alpha +{\tfrac {1}{2}})}(\cos \varphi )}$

або

${\displaystyle C_{n}^{(\alpha )}\left(xy+\gamma {\sqrt {(1-x^{2})(1-y^{2})}}\right)=\sum _{k=0}^{n}{\frac {(\alpha )_{k}(n-k)!}{(\alpha +{\tfrac {1}{2}})_{k}(2k+2\alpha )_{n-k}}}(1-x^{2})^{k/2}\,(1-y^{2})^{k/2}\,C_{n-k}^{(\alpha +k)}(x)\,C_{n-k}^{(\alpha +k)}(y)\,C_{k}^{(\alpha +{\tfrac {1}{2}})}(\gamma )}$

після заміни ${\displaystyle x=\cos \theta ,y=\cos \beta ,\gamma =\cos \varphi }$.

Симетрія відносно операції комплексного спряження:

${\displaystyle C_{n}^{({\bar {\alpha }})}({\bar {z}})={\overline {C_{n}^{(\alpha )}(z)}}.}$

Якщо ${\displaystyle z=x+iy}$, де ${\displaystyle x}$ і ${\displaystyle y}$ — дійсні змінні (${\displaystyle \alpha }$ також дійсне), то дійсна та уявна частини поліномів Ґеґенбауера можуть бути записані в такому вигляді:

${\displaystyle {\rm {Re}}\left[C_{n}^{(\alpha )}(x+{\rm {i}}y)\right]=\sum _{k=0}^{\lfloor n/2\rfloor }{\frac {(-1)^{k}2^{2k}(\alpha )_{2k}}{(2k)!}}\;C_{n-2k}^{(2k+\alpha )}(x)\;y^{2k},}$

${\displaystyle {\rm {Im}}\left[C_{n}^{(\alpha )}(x+{\rm {i}}y)\right]=\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {(-1)^{k}2^{2k+1}(\alpha )_{2k+1}}{(2k+1)!}}\;C_{n-2k-1}^{(2k+\alpha +1)}(x)\;y^{2k+1}.}$

Поліноми Ґеґенбауера природно виникають як узагальнення поліномів Лежандра у теорії потенціалу та гармонічному аналізі. А саме, ньютонівський потенціал в ${\displaystyle \mathbb {R} ^{n}}$ допускає такий розклад:

${\displaystyle {\frac {1}{|\mathbf {x} -\mathbf {y} |^{n-2}}}=\sum _{k=0}^{\infty }{\frac {|\mathbf {x} |^{k}}{|\mathbf {y} |^{k+n-2}}}C_{k}^{(\alpha )}(\mathbf {x} \cdot \mathbf {y} ),\qquad \alpha ={\frac {n-2}{2}},\quad \mathbf {x} \cdot \mathbf {y} =x_{1}y_{1}+\cdots +x_{n}y_{n},\quad \mathbf {x} ,\mathbf {y} \in \mathbb {R} ^{n}.}$

Зокрема, при ${\displaystyle n=3}$ ця формула дає розклад гравітаційного потенціалу по поліномах Лежандра.

Подібні розвинення мають місце для інтегрального ядра у формулі Пуассона для кулі (див. Stein & Weiss, 1971).

Поліноми Ґеґенбауера виникають при знаходженні власних функцій кутової частини ${\displaystyle n}$-вимірного оператора Лапласа і, відповідно, входять до виразу для багатовимірних сферичних (ультрасферичних) гармонік:

${\displaystyle Y_{l}(\Theta )=e^{im_{n-1}\theta _{n-1}}\prod _{k=1}^{n-2}\sin ^{m_{k}}(\theta _{k})C_{m_{k-1}-m_{k}}^{(m_{k}+(n-k)/2)}(\cos \theta _{k}),}$