Послідовність Маєра — Вієторіса

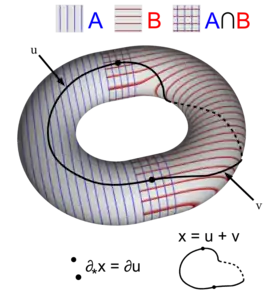
Відображення границі ∂_* може бути задане в такий спосіб.[1] Нехай елемент в H_n (X) представляється n-циклом х, який, при застосуванні барицентричного поділу наприклад, може бути записаний як сума двох n-ланцюгів u і v образи яких лежать повністю в A і B, відповідно. Таким чином, ∂х = ∂(u + v) = 0, так що ∂u = -∂v. Це означає, що образи обох цих граничних (n-1)-циклів містяться в перетині A∩B. Тоді ∂_*([X]) це клас ∂u в H_n-1(A∩B). При цьому вибір розкладу u + v не впливає на [∂u].

Відображення в послідовності залежать від вибору порядку для A і B. Зокрема, границя змінює знак, якщо A і B міняються місцями.

Для редукованих гомологій також задовольняють послідовності Маєра — Вієторіса, в припущенні, що A І B мають непорожній перетин.[2] Послідовність ідентична але закінчується, як:

${\displaystyle \cdots \rightarrow {\tilde {H}}_{0}(A\cap B)\,{\xrightarrow {(i_{*},j_{*})}}\,{\tilde {H}}_{0}(A)\oplus {\tilde {H}}_{0}(B)\,{\xrightarrow {k_{*}-l_{*}}}\,{\tilde {H}}_{0}(X)\rightarrow \,0.}$

Для відносних гомологій послідовність Маєра — Вієторіса записується як:

${\displaystyle \cdots \rightarrow H_{n}(A\cap B,C\cap D)\,{\xrightarrow {(i_{*},j_{*})}}\,H_{n}(A,C)\oplus H_{n}(B,D)\,{\xrightarrow {k_{*}-l_{*}}}\,H_{n}(X,Y)\,{\xrightarrow {\partial _{*}}}\,H_{n-1}(A\cap B,C\cap D)\rightarrow \cdots }$

розклад сфери

Щоб обчислити гомології k-вимірної сфери S^k , нехай A і B півсфери в X з перетином гомотопічно еквівалентним (k−1)-вимірній екваторіальній області. Оскільки k-вимірні півкулі є гомеоморфними k-вимірним кулям, групи гомологій A і B є тривіальними. Натомість їх перетин гомотопічно еквівалентний сфері розмірності (k−1).

Послідовність Маєра — Вієторіса має вигляд
${\displaystyle \cdots \rightarrow 0\rightarrow {\tilde {H}}_{n}\left(S^{k}\right){\xrightarrow {\partial _{*}}}\,{\tilde {H}}_{n-1}\left(S^{k-1}\right)\rightarrow 0\rightarrow \cdots \!}$

З точності послідовності випливає, що гомоморфізм ∂_* є ізоморфізмом. Використовуючи редуковані гомології для 0-сфери (двох точок) в якості бази математичної індукції, одержуємо[3]
${\displaystyle {\tilde {H}}_{n}\left(S^{k}\right)\cong \delta _{kn}\,\mathbb {Z} =\left\{{\begin{matrix}\mathbb {Z} &n=k\\0&n\neq k\end{matrix}}\right.}$[4]

Розклад Пляшки Клейна на дві стрічки Мебіуса, червону і синю.

Для обчислення гомологій пляшки Клейна, запишемо її, як об'єднання двох стрічок Мебіуса A і B склеєних уздовж їх граничної кола . Тоді A, B і їх перетин A∩ B є гомотопно еквівалентними колу. Нетривіальна частина послідовності дає[5]

${\displaystyle 0\rightarrow H_{2}(X)\rightarrow \mathbb {Z} \ {\xrightarrow {\overset {}{\alpha }}}\ \mathbb {Z} \oplus \mathbb {Z} \rightarrow \,H_{1}(X)\rightarrow 0}$

а з інших елементів послідовності випливає рівність нулю гомологій розмірностей більше, ніж 2. Образом 1 при відображенні α є (2, −2) оскільки граничне коло стрічки Мебіуса двічі обертається навколо центрального кола. Зокрема α є ін'єктивним відображенням, тож гомологічна група розмірності 2 також є нульовою. Нарешті, вибираючи (1, 0) і (1, -1) як базис для Z², отримуємо
${\displaystyle {\tilde {H}}_{n}\left(X\right)\cong \delta _{1n}\,(\mathbb {Z} \oplus \mathbb {Z} _{2})=\left\{{\begin{matrix}\mathbb {Z} \oplus \mathbb {Z} _{2}&n=1\\0&n\neq 1\end{matrix}}\right.}$

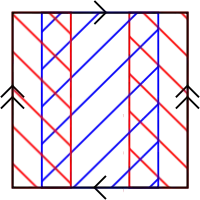
Відображення границі ∂_* на торі, де 1 цикл x = u + v — сума двох 1-ланцюгів, границя якої лежить в перетині A і B.

Нехай ${\displaystyle X=\mathbf {T} ^{n}=S^{1}\times S^{1}}$— звичайний тор. Тоді X = A∪B, де A і B є відкритими підмножинами як зображено на малюнку.

Множини A і B є гомотопно еквівалентними колу і тому їх групи гомологій рівні групам гомологій кола. Натомість A∩B є гомотопно еквівалентним двом окремим колам і тому його групи гомологій є рівними прямим сумам груп для двох кіл. Також ${\displaystyle {\tilde {H}}_{0}(X)\simeq \mathbb {Z} .}$

Нетривіальна частина послідовності для редукований гомологій має вигляд

${\displaystyle 0\rightarrow {\tilde {H}}_{2}(X)\rightarrow \mathbb {Z} \oplus \mathbb {Z} \ {\xrightarrow {\overset {}{\alpha }}}\ \mathbb {Z} \oplus \mathbb {Z} {\xrightarrow {\overset {}{\beta }}}\,{\tilde {H}}_{1}(X){\xrightarrow {\overset {}{\partial ^{*}}}}\mathbb {Z} \rightarrow 0}$

а з інших елементів послідовності випливає рівність нулю гомологій розмірностей більше, ніж 2.

Відображенні α задане як ${\displaystyle \alpha (n,m)=(n+m,-n-m)}$. Ядром цього відображення є підгрупа елементів виду (n, -n), яка є ізоморфною групі цілих чисел. Звідси також ${\displaystyle {\tilde {H}}_{2}(X)\simeq \mathbb {Z} .}$

Образ відображення α відповідно теж є ізоморфним групі цілих чисел, як і образ і ядро відображення β.Як наслідок ядро і образ гомоморфізму ∂_* теж є ізоморфним групі цілих чисел і відповідно ${\displaystyle {\tilde {H}}_{1}(X)\simeq \mathbb {Z} \oplus \mathbb {Z} .}$

Остаточно:

${\displaystyle {\tilde {H}}_{n}\left(S^{1}\times S^{1}\right)=\left\{{\begin{matrix}\mathbb {Z} \oplus \mathbb {Z} &n=1\\\mathbb {Z} &n=2\\0&n\neq 1,2\end{matrix}}\right.}$

Розклад простору X — букета двох сфер сфер K and L. Цей розклад дозволяє обчислити гомологічну групу простору X.

Нехай X буде букет двох просторів K і L, і припустимо, крім того, що виділена точка є деформаційним ретрактом з відкритих околів U ⊂ K і V ⊂ L. Позначивши A = K∪V і B = U∪L одержуємо, що A∪B = X and A∩B = U∪V, які є стягуваними просторами згідно означень. Тоді із редукованої версії послідовності одержуємо:[6]

${\displaystyle {\tilde {H}}_{n}(K\vee L)\cong {\tilde {H}}_{n}(K)\oplus {\tilde {H}}_{n}(L)}$

для всіх розмірностей n.

На малюнку показаний букет двох сфер. Для цього конкретного випадку, використовуючи результат вище для 2-сфер:

${\displaystyle {\tilde {H}}_{n}\left(S^{2}\vee S^{2}\right)\cong \delta _{2n}\,(\mathbb {Z} \oplus \mathbb {Z} )=\left\{{\begin{matrix}\mathbb {Z} \oplus \mathbb {Z} &n=2\\0&n\neq 2\end{matrix}}\right.}$

Якщо простір X є надбудовою SY простору Y, нехай A і B позначають доповнення у X верхньої і нижньої вершин. Тоді X є рівним A∪B і A з B є стягуваними просторами. Перетин A∩B є гомотопно еквівалентним простору Y. Тому із послідовності Маєра — Вієторіса випливає, що для всіх n,[7]

${\displaystyle {\tilde {H}}_{n}(SY)\cong {\tilde {H}}_{n-1}(Y)}$

This decomposition of the suspension X of the 0-sphere Y yields all the homology groups of X.

На малюнку справа показано, що коло X є надбудовою простору Y двох точок. Загалом k-сфера є надбудовою (k − 1)-сфери і звідси знову можна отримати вираз для гомологічних груп сфер.