Структура спільноти
У вивченні складних мереж, кажуть, що мережа має структуру спільноти, якщо вузли мережі можна легко згрупувати в такі множини (які можливо мають перетин), що кожний набір вузлів щільно пов'язаний між собою всередині. У випадку коли множини розбиття вузлів, не перетинаються, кажуть, що мережа природно ділиться на групи із щільними внутрішніми та слабкими зовнішніми зв'язками. Проте перетин спільнот також є допустимим. Більш загальне означення базується на такому принципі: пара вузлів ймовірніше має зв'язок, якщо дані вузли є членами однієї спільноти, і менш імовірно, що пара вузлів пов'язана, якщо вони не входять до однієї спільноти. Пов'язаною задачею, але трохи відмінною від даної, є пошук спільноти, до якої належить певна вершина.
| Наука про мережі | ||||
|---|---|---|---|---|
|
||||
| Види мереж | ||||
|
||||
| Графи | ||||
|
||||
| ||||
|
||||
| Моделі | ||||
|
||||
| ||||
|
||||
Властивості
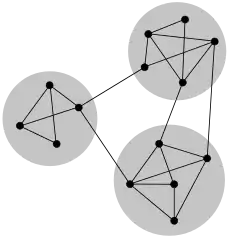
У дослідженні мереж, таких, як комп'ютерні та інформаційні мережі, соціальні та біологічні мережі, виявлено велику кількість різних характеристик, включаючи з поміж інших характеристику тісного світу, безмасштабності мережі та кластеризацію. Іншою спільною характеристикою є структура спільности.[1][2][3][4][5] У контексті мереж, структура спільности посилається на те, що виникнення груп вузлів у мережі є характерним для щільно зусереджених внутрішніх зв'язків спільноти та слабо розгалужених — зовнішніх. Така неоднорідність опису мережі говорить про те, що в мережі існує певна природна класифікація.
Спільноти часто визначаються в термінах розділення на множини вершин, тобто кожен вузол належить виключно до однієї спільноти, як на схемі. Це корисне спрощення, і більшість методів по знаходженню спільнот використовують даний підхід. У той час як, в деяких випадках, кращим представленням мережі є таким чиином, щоб вершини належали більше ніж одній спільноті. Такий випадок зустрічається, наприклад, у соціальних мережах, де кожна вершина являє собою людину, а спільноти — різні групи друзів: одна спільнота — родина, інша — співробітники, ще інша — друзі із спорт-клуба і т. д. Використання кліків для визначення спільнот, що обговорено нижче, — це лише один приклад того, як можна знайти перетинні множини.
Деякі мережі можуть не мати суттєвої структури спільноти. Багато основних мережевих моделей, наприклад, випадкові графи та модельБарабаші — Альберт не мають структури спільноти.
Актуальність
Структура спільнот — досить поширена у справжніх мережах. Соціальні мережі включають спільні групи (походження терміну, фактично), основою яких є спільні інтереси, місця, професії, і т. д.[6]
Із ряду причин, важливим є пошук основної спільноти в структурі мережі, якщо, звісно, така існує. Спільноти дозволяють нам створювати масштабну карту мережі, оскільки окремі структури ведуть себе як мета-вузли (англ. meta-nodes) у мережі, що полегшує її вивчення.[7]
Окремі спільноти також висвітлюють роботу системи, оскільки спільноти часто відповідають її функціональними часточками. У метаболічних мережах, таким функціональним групам відповідають цикли або шляхи, у той час як, в мережі із взаємодією з білками, спільнотам, відповідають білки із схожим функціоналом всередині біологічної клітини. Аналогічно, мережі цитат утворюють спільноту за темою дослідження. Можливість ідентифікувати ці структури всередині мережі може надати уявлення того, як мережева функція й топологія впливають один на одного. Таке розуміння може бути корисним для вдосконалення деяких алгоритмів для графів, таких як спектральна кластеризація.[8]
Вагомою причиною того, що спільноти важливі є те, що часто дуже відмінні властивості від усереднених по мережі, мають спільноти, розглядаючи їх окремо одна від одної. Таким чином, лише виділення усереднених властивостей втрачає багато важливих і цікавих функцій у середині самої системи. Наприклад, у випадку соціальних мереж, одночасно можуть існувати дві групи: компанійські та мовчазні.
Існування спільнот також зазвичай впливає на різні процеси, такі як розповсюдження чуток або розповсюдження епідемії в мережі. Тому для правильного розуміння таких процесів важливо виявити спільноти, а також вивчати, як вони впливають на процеси поширення в різних умовах.
Нарешті, важливим застосуванням, що виявило спільноту в мережевій науці, є прогноз відсутніх зв'язків та виявлення помилкових зв'язків у мережі. Під час вимірювання, деякі зв'язки можуть не спостерігаються з ряду причин. Точно так само, деякі зв'язки можуть помилково надавати дані через помилки при вимірюванні. З обома випадками успішно справляється алгоритм виявлення спільноти, оскільки це дозволяє визначити ймовірність існування ребра між даною парою вузлів.[9]
Алгоритми по знаходженню спільнот
Пошук спільнот у довільній мережі може бути обчислювально складним завданням. Кількість спільнот, якщо така існує, в мережі, як правило, невідома, і в спільнотах часто існує неоднорідний розмір та/або щільність. Проте, незважаючи на ці труднощі, розроблено та застосовано кілька методів пошуку спільнот із різною точністю
Метод найменшого розрізу
Одним із найдавніших алгоритмів розподілу мереж на частини є метод найменшого розрізу(і варіанти, такі як коефіцієнт розрізу та нормований розріз). Застосування даного методу можна побачити, наприклад, в балансуванні навантаження для паралельних обчислень, з метою мінімізації зв'язків між процесорними вузлами.
У методі мінімального розрізу мережа ділиться на заздалегідь визначену кількість частин, як правило, приблизно такого ж розміру, які вибираються таким чином, щоб мінімізувати кількість ребер між групами. Цей метод добре працює в багатьох прикладних задачах, для яких він спочатку був призначений, але менш ідеально підходить для пошуку структури спільноти в загальних мережах, оскільки він знайде спільноти незалежно від того, чи вони неявні, чи ні в структурі, а знайде лише фіксоване число їх.[10]
Ієрархічна кластеризація
Інший спосіб пошуку структур спільноти в мережах — це ієрархічна кластеризація. У даному методі визначається міра подібності, яка кількісно визначає деякий (зазвичай топологічний) тип подібності між парами вузлів. Найбльш вживані міри це косинус подібності, коефіцієнт Джакарда та відстань Хеммінга для матриці суміжності. Тоді група подібних вузлів об'єднується відповідно до цієї міри. Існує декілька загальних схем для здійснення групування, дві найпростіші — кластеризація з одним зв'язком, у якій дві групи вважаються окремими спільнотами тоді і тільки тоді, коли всі пари вузлів у різних групах мають схожість нижче заданого порогу, і повна кластеризація зв'язків, у якій всі вузли всередині кожної групи мають подібність більшу, ніж порогові. Новий підхід у цьому напрямку полягає у застосуванні різних мір схожості або невідповідності, об'єднаних за допомогою опуклих сум, що значно покращило ефективність даної методики
Алгоритм Гірван — Ньюмана
Іншим широко вживаним алгоритмом для пошуку спільнот є алгоритм Гірвана-Ньюмана. Цей алгоритм ідентифікує ребра в мережі, що лежать між спільнотами, а потім їх видаляє, залишивши лише самі спільноти. Ідентифікація виконується за допомогою централізованості гранично-теоретичної міри, яка присвоює номер кожному ребру, якщо край лежить «між» багатьма парами вузлів.
Алгоритм Гірвана-Ньюмана повертає результати прийнятної якості і популярний, оскільки він був реалізований у ряді стандартних програмних пакетів. Але він також працює повільно, витрачаючи O(m2n) часу на мережу з n вершин і m-ребер, що робить це недоцільним для мереж з більш ніж кількома тисячами вузлів.[11]
Максимізація модульності
Незважаючи на свої відомі недоліки, одним з найпоширеніших методів виявлення спільнот є максимізація модульності (англ. modularity maximization). Модульність — це функція вигоди, яка вимірює якість певного поділу мережі на спільноти. Метод максимізації модульності виявляє спільноти шляхом пошуку можливого поділу мережі на одну або декілька спільнот, що мають особливо високу модульність. Оскільки вичерпний пошук над усіма можливими підрозділами, як правило, неможливий, практичні алгоритми базуються на наближених методах оптимізації, таких як жадібні алгоритми, алгоритм імітації відпалу або спектральна оптимізація, з різними підходами, що пропонують різні баланси між швидкістю та точністю..[12][13] Найпопулярніший підхід до максимізації модульності — це метод Лувена, який ітеративно оптимізує локальні спільноти, доки не може бути вдосконалена глобальна модульність, з урахуванням збурення поточної спільноти.[14][15] Нині найкращий алгоритм максимізації модульності (переможець 10-го змагання з реалізації Центру дискретної математики та теоретичної обчислювальної техніки, англ. the 10th DIMACS Implementation Challenge) — це ітеративний ансамблевий алгоритм.[16]
Корисність оптимізації модульності є сумнівною, оскільки було показано, що оптимізація модульності часто не дозволяє виявляти кластери менші, ніж певна шкала, залежно від розміру мережі (межа точності[17]); з іншого боку, множина значень модульності характеризується величезною виродженістю частин із високою модулярністю, близькими до абсолютного максимуму, які можуть дуже відрізнятися один від одного.[18]
Статистичний висновок
Методи, засновані на статистичному висновуванні намагаються підібрати породжувальну модель для даних мережі. Загальна перевага цього підходу, у порівнянні з альтернативами, — це її більш принциповий характер і здатність по своїй суті розглядати питання статистичної значущості. Більшість методів у літературі базуються на основі стохастичної блокової моделі[19], а також є варіанти, що включають змішане членство,[20][21] корегування розмірності,[22] й ієрархічну структурність.[23] Обрати модель можна, використовуючи в якості головного наближення таке, що має мінімальну довжину опису[24][25] (або еквівалентно, коефіцієнт Байєса[26]) та перевіркою відношення максимальної правдоподібності.[27] Наразі існує багато алгоритмів для ефективного виведення випадкових блокових моделей, включаючи алгоритм поширення довіри[28][29] та агломераційний Монте Карло.[30]
На відміну від підходів, які намагаються скомпонувати мережу з об'єктивною функцією, цей клас методів ґрунтується на генеративних моделях, які не тільки служать описом великомасштабної структури мережі, але також можуть бути використані для узагальнення даних і прогнозування появи пропущених або хибних зв'язків у мережі.[31][32]
Методи на основі кліки
Кліка — це підграф, у якому кожен вузол пов'язаний з кожним іншим вузлом кліки. Оскільки вузли не можуть бути більш тісно пов'язаними, ніж в описаному випадку, не дивно, що існує багато підходів до виявлення спільнот у мережах, заснованих на виявленні кліків у графі та аналізі того, як вони збігаються. Варто зауважити, що оскільки вузол може бути членом більш ніж однієї кліки, то вузол може бути членом декількох спільнот, за даним методом, останнє висвітлює структуру спільнот, що перетинаються.
Один з методів — знайти максимальні кліки, тобто знайти кліки, які не є підграфом будь-якої іншої кліки. Класичним алгоритмом їх пошуку є алгоритм Брона-Кербоша. Перетин може використовуватися для визначення спільнот кількома способами. Найпростіше розглянути лише максимальні кліки, більші за мінімальний розмір (кількість вузлів). Об'єднання цих кліків потім визначає підграф, чиї компоненти (роз'єднані частини) визначають спільноти.[33] Такі підходи часто застосовуються у програмному забезпеченні аналізу соціальних мереж, таких як UCInet.
Альтернативний підхід до використання кліків фіксованого розміру, . Перетин може бути використаний для визначення типу -регулярного гіперграфу або структури, яка є узагальненням лінійного графу (випадку, коли ) відомою як граф кліки (англ. Clique graph).[34] Графи клік мають вершини, які представляють кліки у початковому графі, а ребра графу кліки враховують накладання кліки у початковому графі. Застосовуючи будь-який з попередніх методів виявлення спільноти (які присвоюють кожному вузлу спільноту) до графу кліки, отримаємо, що кожній кліці буде присвоєно спільноту. Це можна використати для визначення членства спільноти в вузлах кліки. Знову ж таки, оскільки вузол може бути в декількох кліках, то він може бути членом кількох спільнот. Наприклад, метод фільтрування кліки[35] визначає спільноти як фільтрування кластерів k-клік. Для цього він знаходить всі k-кліки в мережі, тобто всі повні підграфи. Потім він визначає, що два k-кліка — сусідні, якщо вони поділяють вузол, тобто це використовується для визначення ребер у крафі кліка. Тоді спільнота визначається як максимальна сукупність -клік у яких можна досягти -кліку із будь-якої іншої -кліки через -клік сусідніх. Тобто спільноти — це лише пов'язані компоненти в графі кліка. Оскільки вузол може одночасно належать до кількох різних кластерів -кліки, то спільноти можуть перетинатися.
Тестування методів пошуку алгоритмів спільнот
Оцінка алгоритмів, для виявлення структур спільноти, все ще залишається відкритим питанням. Очевидно, що повинна базуватися на аналізі мереж відомих структур. Типовим прикладом є тест «чотири групи», в якому мережа поділяється на чотири групи однаково великих розмірів (зазвичай по 32 вузла кожна), а ймовірність зв'язку в межах та між групами змінюється, щоб створювати більш-менш складні структури для виявлення алгоритмів. Такі тестові графи — це особливий випадок висадженої моделі l-поділу (англ. planted l-partition model)[36] Анни Кондон та Річарда Карпа, або більш загального випадку «стохастичних блокових моделей», загального класу моделей випадкових мереж, що містить структуру спільноти. Були запропоновані інші більш гнучкі орієнтири, що дозволяють використовувати різні групи розмірів та нетривіальні розподіли ступенів, такі як тест LFR benchmark, запропонований Ланченетті,[37] що є розширенням чотирьох груп тестів, і включає гетерогенні розподіли ступеня вузла та розміру спільноти, що робить його більш сильним тестом методів виявлення спільнот. Важливим є питання, поставлене Касимом Пастом і Фаразом Заіді в їх роботі щодо визначення алгоритмів виявлення спільнот на еталонних моделях на основі динаміки еволюції замість моделей конфігурації.[38]
Найбільш поширені комп'ютерні тести починаються з мережі чітко визначених спільнот. Тоді ця структура деградується шляхом перекручування або видалення посилань, і для алгоритмів стає все важчим і важчим визначення початкового розподілу. Врешті, мережа досягає точки, де вона, по суті, є випадковою. Цей тип тесту можна назвати «відкритим». Продуктивність таких тестів оцінюється нормалізованою взаємною інформацією або варіацією інформації. Вони порівнюють результати, отримані алгоритмом з оригінальною структурою спільноти, оцінюючи подібність обох розділів.
Виявлення
Протягом останніх років досить неочікуваний результат був отриманий різними групами, який показує фазовий перехід у проблемі виявлення спільнот: щільність зв'язків усередині спільнот та між спільнотами стає все більш рівномірною або меншою (еквівалентно, оскільки структура спільноти стає занадто слабкою або мережа стає надто рідкою), несподівано спільноти стають невизначеними. У певному сенсі, самі спільноти все ще існують, оскільки наявність і відсутність зв'язків все ще співвідносяться з членством спільноти та їх крайніх точок; але тоді стає інформаційно -теоретично неможливим позначати вузли краще, ніж за допомогою ймовірності, або навіть відрізнити граф від створеного нульовою моделлю, такою як модель Erdos-Renyi без структури спільноти. Цей перехід не залежить від типу алгоритму, який використовується для виявлення спільнот, тобто існує фундаментальна межа нашої здатності виявляти спільноти в мережах навіть за оптимального байєсівського висновку (тобто незалежно від наших обчислювальних ресурсів).[39][40][41]
Розглянемо стохастичниу блокову модель, що має всього вузлів, gгрупи однакового розміру, і нехай та — ймовірності зв'язку в групах та за межами спільнот відповідно. Якщо , ця мережа матиме структуру спільноти, оскільки щільність зв'язку всередині груп буде більше, ніж щільність зв'язків між групами. Рідко, та співвідносяться як так що середній ступінь є сталою:
Тоді стає неможливим виявити спільноти якщо:[40]
Див. також
Посилання
- M. Girvan; M. E. J. Newman (2002). Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 99 (12): 7821–7826. PMC 122977. PMID 12060727. doi:10.1073/pnas.122653799.
- S. Fortunato (2010). Community detection in graphs. Phys. Rep. 486 (3–5): 75–174. doi:10.1016/j.physrep.2009.11.002.
- F. D. Malliaros; M. Vazirgiannis (2013). Clustering and community detection in directed networks: A survey. Phys. Rep. 533 (4): 95–142. doi:10.1016/j.physrep.2013.08.002.
- M. A. Porter; J.-P. Onnela; P. J. Mucha (2009). Communities in Networks. Notices of the American Mathematical Society 56: 1082–1097, 1164–1166.
- Fani, Hossein; Bagheri, Ebrahim (2017). «Community detection in social networks». Encyclopedia with Semantic Computing and Robotic Intelligence. 1. pp. 1630001 [8]. doi:10.1142/S2425038416300019. http://www.worldscientific.com/doi/abs/10.1142/S2425038416300019.
- Hamdaqa, Mohammad; Tahvildari, Ladan; LaChapelle, Neil; Campbell, Brian (2014). Cultural Scene Detection Using Reverse Louvain Optimization. Science of Computer Programming 95: 44–72. doi:10.1016/j.scico.2014.01.006.
- M.E.J.Neman. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 74 (3): 1–19. doi:10.1103/PhysRevE.74.036104.
- Zare, Habil; P. Shooshtari; A. Gupta; R. Brinkman (2010). Data reduction for spectral clustering to analyze high throughput flow cytometry data. BMC Bioinformatics 11 (1): 403. PMC 2923634. PMID 20667133. doi:10.1186/1471-2105-11-403.
- Aaron Clauset; Cristopher Moore; M.E.J. Newman. Hierarchical structure and the prediction of missing links in networks. Nature 453 (7191): 98–101. PMID 18451861. doi:10.1038/nature06830.
- M. E. J. Newman (2004). Detecting community structure in networks. Eur. Phys. J. B 38 (2): 321–330. doi:10.1140/epjb/e2004-00124-y.
- M. E. J. Newman (2004). Fast algorithm for detecting community structure in networks. Phys. Rev. E 69 (6): 066133. doi:10.1103/PhysRevE.69.066133.
- L. Danon; J. Duch; A. Díaz-Guilera; A. Arenas (2005). Comparing community structure identification. J. Stat. Mech. 2005 (09): P09008. doi:10.1088/1742-5468/2005/09/P09008.
- R. Guimera; L. A. N. Amaral (2004). Functional cartography of complex metabolic networks. Nature 433 (7028): 895–900. PMC 2175124. PMID 15729348. doi:10.1038/nature03288.
- V.D. Blondel; J.-L. Guillaume; R. Lambiotte; E. Lefebvre (2008). Fast unfolding of community hierarchies in large networks. J. Stat. Mech. 2008 (10): P10008. doi:10.1088/1742-5468/2008/10/P10008.
- Lightning-fast Community Detection in Social Media: A Scalable Implementation of the Louvain Algorithm (PDF). 2013.
- Michael Ovelgönne; Andreas Geyer-Schulz (2013). An ensemble learning strategy for graph clustering. Graph Partitioning and Graph Clustering. Contemporary Mathematics (American Mathematical Society) 588: 187–206. doi:10.1090/conm/588.
- S. Fortunato; M. Barthelemy (2007). Resolution limit in community detection. Proceedings of the National Academy of Sciences of the United States of America 104 (1): 36–41. PMC 1765466. PMID 17190818. doi:10.1073/pnas.0605965104.
- B. H. Good; Y.-A. de Montjoye; A. Clauset (2010). The performance of modularity maximization in practical contexts. Phys. Rev. E 81 (4): 046106. doi:10.1103/PhysRevE.81.046106.
- Holland, Paul W.; Kathryn Blackmond Laskey; Samuel Leinhardt (June 1983). Stochastic blockmodels: First steps. Social Networks 5 (2): 109–137. ISSN 0378-8733. doi:10.1016/0378-8733(83)90021-7. Процитовано 26 серпня 2011.
- Airoldi, Edoardo M.; David M. Blei; Stephen E. Fienberg; Eric P. Xing (June 2008). Mixed Membership Stochastic Blockmodels. J. Mach. Learn. Res. 9: 1981–2014. ISSN 1532-4435. Процитовано 9 жовтня 2013.
- Ball, Brian; Brian Karrer; M. E. J. Newman (2011). Efficient and principled method for detecting communities in networks. Physical Review E 84 (3): 036103. doi:10.1103/PhysRevE.84.036103. Процитовано 8 грудня 2011.
- Karrer, Brian; M. E. J. Newman (21 січня 2011). Stochastic blockmodels and community structure in networks. Physical Review E 83 (1): 016107. doi:10.1103/PhysRevE.83.016107. Процитовано 8 листопада 2011.
- Peixoto, Tiago P. (24 березня 2014). Hierarchical Block Structures and High-Resolution Model Selection in Large Networks. Physical Review X 4 (1): 011047. doi:10.1103/PhysRevX.4.011047. Процитовано 24 квітня 2014.
- Martin Rosvall; Carl T. Bergstrom (2007). An information-theoretic framework for resolving community structure in complex networks. Proceedings of the National Academy of Sciences of the United States of America 104 (18): 7327–7331. PMC 1855072. PMID 17452639. doi:10.1073/pnas.0611034104.
- P. Peixoto, T. (2013). Parsimonious Module Inference in Large Networks. Phys. Rev. Lett. 110: 148701. Bibcode:2013PhRvL.110n8701P. doi:10.1103/PhysRevLett.110.148701.
- P. Peixoto, T. (2017). Bayesian stochastic blockmodeling. arXiv:1705.10225.
- Yan, Xiaoran; Jacob E. Jensen; Florent Krzakala; Cristopher Moore; Cosma Rohilla Shalizi; Lenka Zdeborova; Pan Zhang; Yaojia Zhu (17 липня 2012). Model Selection for Degree-corrected Block Models. Journal of Statistical Mechanics: Theory and Experiment 2014: P05007. arXiv:1207.3994. doi:10.1088/1742-5468/2014/05/P05007.
- Gopalan, Prem K.; David M. Blei (3 вересня 2013). Efficient discovery of overlapping communities in massive networks. Proceedings of the National Academy of Sciences 110 (36): 14534–14539. ISSN 0027-8424. PMC 3767539. PMID 23950224. doi:10.1073/pnas.1221839110. Процитовано 9 жовтня 2013.
- Decelle, Aurelien; Florent Krzakala; Cristopher Moore; Lenka Zdeborová (12 грудня 2011). Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications. Physical Review E 84 (6): 066106. doi:10.1103/PhysRevE.84.066106. Процитовано 16 січня 2012.
- Peixoto, Tiago P. (13 січня 2014). Efficient Monte Carlo and greedy heuristic for the inference of stochastic block models. Physical Review E 89 (1): 012804. doi:10.1103/PhysRevE.89.012804. Процитовано 21 січня 2014.
- Guimerà, Roger; Marta Sales-Pardo (29 грудня 2009). Missing and spurious interactions and the reconstruction of complex networks. Proceedings of the National Academy of Sciences 106 (52): 22073–22078. PMC 2799723. PMID 20018705. doi:10.1073/pnas.0908366106. Процитовано 9 листопада 2011.
- Clauset, Aaron; Cristopher Moore; M. E. J. Newman (1 травня 2008). Hierarchical structure and the prediction of missing links in networks. Nature 453 (7191): 98–101. ISSN 0028-0836. PMID 18451861. doi:10.1038/nature06830.
- M.G. Everett; S.P. Borgatti (1998). Analyzing Clique Overlap Connections. Connections 21: 49.
- T.S. Evans (2010). Clique Graphs and Overlapping Communities. J. Stat. Mech. 2010 (12): P12037. arXiv:1009.0638. doi:10.1088/1742-5468/2010/12/P12037.
- G. Palla; I. Derényi; I. Farkas; T. Vicsek (2005). Uncovering the overlapping community structure of complex networks in nature and society. Nature 435 (7043): 814–818. PMID 15944704. doi:10.1038/nature03607.
- Condon, A.; Karp, R. M. (2001). Algorithms for graph partitioning on the planted partition model. Random Struct. Algor. 18 (2): 116–140. doi:10.1002/1098-2418(200103)18:2<116::AID-RSA1001>3.0.CO;2-2.
- A. Lancichinetti; S. Fortunato; F. Radicchi (2008). Benchmark graphs for testing community detection algorithms. Phys. Rev. E 78 (4): 046110. doi:10.1103/PhysRevE.78.046110.
- M. Q. Pasta; F. Zaidi (2017). «Leveraging Evolution Dynamics to Generate Benchmark Complex Networks with Community Structures». arXiv:1606.01169 [cs.SI].
- Reichardt, J.; Leone, M. (2008). (Un)detectable Cluster Structure in Sparse Networks. Phys. Rev. Lett. 101 (078701): 1–4. Bibcode:2008PhRvL.101g8701R. doi:10.1103/PhysRevLett.101.078701.
- Decelle, A.; Krzakala, F.; Moore, C.; Zdeborova, L. (2011). Inference and Phase Transitions in the Detection of Modules in Sparse Networks. Phys. Rev. Lett. 107 (065701): 1–5. Bibcode:2011PhRvL.107f5701D. doi:10.1103/PhysRevLett.107.065701.
- Nadakuditi, R.R; Newman, M.E.J. (2012). Graph Spectra and the Detectability of Community Structure in Networks. Phys. Rev. Lett. 108 (188701): 1–5. Bibcode:2012PhRvL.108r8701N. doi:10.1103/PhysRevLett.108.188701.