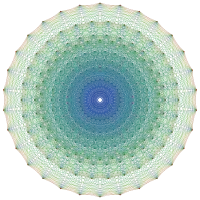
E₈ (математика)

${\displaystyle E_{8}}$ має ранг 8 і розмірність 248 (як многовид). Вектори системи коренів визначені у восьми вимірах.

Схема Динкіна для E₈ має вид

Ця схема коротко описує будову системи коренів. Кожен вузол схеми являє собою простий корінь. Лінія, що з'єднує два простих кореня, означає, що вони знаходяться під кутом 120° один до одного. Два простих кореня, що не з'єднані лінією, ортогональні.

Матриця Картана системи коренів порядку r — це матриця ${\displaystyle r\times r}$, елементи якої визначаються простими коренями в такий спосіб:

${\displaystyle A_{ij}=2{\frac {(\alpha _{i},\alpha _{j})}{(\alpha _{i},\alpha _{i})}}}$

де ${\displaystyle (\cdot ,\cdot )}$ — евклідовий скалярний добуток, а ${\displaystyle \alpha _{i}}$ — прості корені. Елементи матриці не залежать від вибору простих коренів (з точністю до порядку).

Матриця Картана для E₈ має вид

${\displaystyle \left[{\begin{smallmatrix}2&-1&0&0&0&0&0&0\\-1&2&-1&0&0&0&0&0\\0&-1&2&-1&0&0&0&-1\\0&0&-1&2&-1&0&0&0\\0&0&0&-1&2&-1&0&0\\0&0&0&0&-1&2&-1&0\\0&0&0&0&0&-1&2&0\\0&0&-1&0&0&0&0&2\end{smallmatrix}}\right]}$

Визначник цієї матриці дорівнює 1.

• «Ну очень большой результат», Компьютерра, Галактион Андреев, 11 апреля 2007 года
• «В 248-мерное пространство прорвались теоретики», Cnews, 20 марта 2007 года