Гіперболоїдна модель
Гіперболо́їдна моде́ль, відома також як моде́ль Мінко́вського або ло́ренцева моде́ль модель n-вимірної геометрії Лобачевського, в якій кожну точку представлено точкою на верхній поверхні двопорожнинного гіперболоїда в (n+1)-вимірному просторі Мінковського а m-площини представлено перетином (m+1)-площин у просторі Мінковського з S+. Функція гіперболічної відстані в цій моделі задовольняє простому виразу. Гіперболоїдна модель n-вимірного гіперболічного простору тісно пов'язана з моделлю Бельтрамі — Кляйна і дисковою моделлю Пуанкаре, оскільки вони є проєктивними моделями в сенсі, що група рухів є підгрупою проєктивної групи.
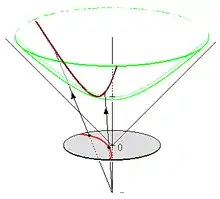
Квадратична форма Мінковського
Якщо є векторами в (n + 1)-вимірному координатному просторі , квадратична форма Мінковського визначається як
Вектори , такі, що , утворюють n-вимірний гіперболоїд S, що складається з двох зв'язаних компонент, або листків - верхній, або майбутнє, лист , де і нижній, або минуле, лист , де . Точки n-вимірної гіперболоїдної моделі є точками на листку майбутнього .
Білінійна форма Мінковського B є поляризацією квадратичної форми Мінковського Q,
Або в явному вигляді,
Гіперболічна відстань між двома точками u і v простору задають формулою ,
Прямі
Пряма в гіперболічному n-просторі моделюється геодезичною на гіперболоїді. Геодезична на гіперболоїді є (непорожнім) перетином з двовимірним лінійним підпростором (включно з початком координат) n+1-вимірного простору Мінковського. Якщо ми візьмемо як u і v базисні вектори лінійного підпростору з
і використаємо w як параметр для точок на геодезичній, то
буде точкою на геодезичній[1].
Загальніше, k-вимірна «площина» в гіперболічному n-просторі моделюватиметься (непорожнім) перетином гіперболоїда з k+1-вимірним лінійним підпростором (включно з початком координат) простору Мінковського.
Рухи
Невизначена ортогональна група O(1,n), звана також (n+1)-вимірною групою Лоренца, є групою Лі дійсних (n+1)×(n+1) матриць, яка зберігає білінійну форму Мінковського. Іншими словами, це група лінійних рухів простору Мінковського. Зокрема, ця група зберігає гіперболоїд S. Нагадаємо, що невизначені ортогональні групи мають чотири зв'язані компоненти, які відповідають оберненню або збереженню орієнтації на кожному підпросторі (тут — 1-вимірному і n-вимірному), і утворюють 4-групу Кляйна. Підгрупа O(1,n), яка зберігає знак першої координати, є ортохронною групою Лоренца, що позначається O+(1,n), і має дві компоненти, які відповідають збереженню або оберненню орієнтації підпростору. Її підгрупа SO+(1,n), що складається з матриць з визначником одиниця, є зв'язаною групою Лі розмірності n(n+1)/2, яка діє на S+ лінійними автоморфізмами і зберігає гіперболічну відстань. Ця дія транзитивна і є стабілізатором вектора (1,0,…, 0), що складається з матриць вигляду
де належить до компактної спеціальної ортогональної групи SO(n) (яка узагальнює групу обертань SO(3) для n = 3). Звідси випливає, що n-вимірний гіперболічний простір можна подати як однорідний простір і Ріманів симетричний простір рангу 1,
Група SO+(1,n) є повною групою рухів n-вимірного гіперболічного простору, що зберігають орієнтацію.
Історія
- У кількох статтях між 1878 і 1885 Вільгельм Кіллінг[2][3][4] використав подання геометрії Лобачевського, яке він приписує Карлу Веєрштрассу. Зокрема, він обговорює квадратичні форми, такі як або для довільних розмірностей , де є двоїстою мірою кривини, означає Евклідову геометрію, еліптичну геометрію, а означає гіперболічну геометрію.
- За Джеремі Ґреєм (1986)[5] Пуанкаре використав гіперболоїдну модель у його персональних нотатках 1880 року. Пуанкаре опублікував свої результати в 1881, у яких він обговорює інваріантність квадратичної форми [6]. Ґрей показує, де гіперболоїдна модель явно згадується в пізніших роботах Пуанкаре[7]. Докладніше див. Історія перетворень Лоренца, розділ «Пуанкаре».
- Також Гомершем Кокс у 1882[8][9] використав координати Веєрштрасса (без зазначення цього імені), що задовольняють співвідношенню , а також співвідношенню .
- Далі модель використали Альфред Клебш і Фердинанд фон Ліндеман 1891 року при обговоренні співвідношень і [10].
- Координати Веєрштрасса використовували також Ґерард (1892), Гаусдорф (1899), Вудс (1903) і Лібман (1905).
Пізніше (1885) Кілінг стверджував, що фраза координати Веєрштрасса співвідноситься з елементами гіперболоїдної моделі так: якщо задано скалярний добуток на , координати Веєрштрасса точки дорівнюють
що можна порівняти з виразом
для моделі півсфери[11].
Як метричний простір гіперболоїд розглядав Александер Макфарлейн у книзі Papers in Space Analysis (1894). Він зауважив, що точки на гіперболоїді можна записати як
де α є базисним вектором, ортогональним до осі гіперболоїда. Наприклад, він отримав гіперболічний закон косинусів, використавши алгебри фізики[1].
Х. Дженсен сфокусувався на гіперболоїдній моделі в статті 1909 року «Подання гіперболічної геометрії на двопорожнинному гіперболоїді»[12]. 1993 року У. Ф. Рейнольдс виклав ранню історію моделі в статті, надрукованій у журналі American Mathematical Monthly[13].
Як загальновизнану модель у XX столітті, її ототожнив з Geschwindigkeitsvectoren (нім. векторами швидкості) Герман Мінковський у просторі Мінковського. Скотт Вальтер у статті 1999 року «Неевклідів стиль спеціальної теорії відносності»[14] згадує обізнаність Мінковського, але виводить походження моделі від Гельмгольца, а не від Веєрштрасса чи Кіллінга.
У ранні роки Владимир Варичак використовував релятивістську гіперболоїдну модель для пояснення фізики швидкості. У його доповіді в Німецькому математичному товаристві 1912 року він посилався на координати Веєрштрасса[15].
Див. також
- Конформно-евклідова модель
- Гіперболічний кватерніон
Примітки
- Macfarlane, 1894.
- Killing, 1878, с. 72-83.
- Killing, 1880, с. 265-287.
- Killing, 1885.
- Gray, 1986, с. 271-2.
- Poincaré, 1881, с. 132 -138.
- Poincaré, 1887, с. 71-91.
- Cox, 1881, с. 178-192.
- Cox, 1882, с. 193-215.
- Lindemann, 1891, с. 524.
- Deza E., Deza M., 2006.
- Jansen, 1909, с. 409-440.
- Reynolds, 1993, с. 442-55.
- Scott, 1999, с. 91–127.
- Varićak, 1912, с. 103–127.
Література
- Killing W. Ueber zwei Raumformen mit constanter positiver Krümmung // Journal für die reine und angewandte Mathematik. — 1878. — Т. 86 (25 грудня). — С. 72-83.
- Killing W. Die Rechnung in den Nicht-Euklidischen Raumformen // Journal für die reine und angewandte Mathematik. — 1880. — Т. 89 (25 грудня). — С. 265-287.
- Killing W. Die nicht-euklidischen Raumformen. — Leipzig, 1885.
- Jeremy Gray. Linear differential equations and group theory from Riemann to Poincaré. — 1986. — С. 271-2.
- Poincaré H. Sur les applications de la géométrie non-euclidienne à la théorie des formes quadratiques // Association française pour l'avancement des sciences. — 1881. — Т. 10 (25 грудня). — С. 132 -138.
- Poincaré H. On the fundamental hypotheses of geometry // Collected works. — 1887. — Т. 11. — С. 71-91.
- Cox H. Homogeneous coordinates in imaginary geometry and their application to systems of forces // The quarterly journal of pure and applied mathematics. — 1881. — Т. 18, вип. 70 (25 грудня). — С. 178-192.
- Cox H. Homogeneous coordinates in imaginary geometry and their application to systems of forces (continued) // The quarterly journal of pure and applied mathematics. — 1882. — Т. 18, вип. 71 (25 грудня). — С. 193-215.
- Lindemann F. Vorlesungen über Geometrie von Clebsch II = 1890. — Leipzig, 1891. — С. 524.
- Elena Deza, Michel Deza. Dictionary of Distances. — 2006.
- Jansen H. Abbildung hyperbolische Geometrie auf ein zweischaliges Hyperboloid // Mitt. Math. Gesellsch Hamburg. — 1909. — Вип. 4 (25 грудня). — С. 409-440.
- Alexander Macfarlane. Papers on Space Analysis. — New York : B. Westerman, 1894.
- Alekseevskij D.V., Vinberg E.B., Solodovnikov A.S. Geometry of Spaces of Constant Curvature. — Berlin, New York : Springer-Verlag, 1993. — (Encyclopaedia of Mathematical Sciences) — ISBN 3-540-52000-7.
- James Anderson. Hyperbolic Geometry. — 2nd. — Berlin, New York : Springer-Verlag, 2005. — (Springer Undergraduate Mathematics Series) — ISBN 978-1-85233-934-0.
- John G. Ratcliffe. Глава 3 // Foundations of hyperbolic manifolds. — Berlin, New York : Springer-Verlag, 1994. — ISBN 978-0-387-94348-0.
- Miles Reid, Balázs Szendröi. Geometry and Topology. — Cambridge University Press, 2005. — С. Figure 3.10, p 45. — ISBN 0-521-61325-6.
- Patrick J. Ryan. Euclidean and non-Euclidean geometry: An analytical approach. — Cambridge, London, New York, New Rochelle, Melbourne, Sydney : Cambridge University Press, 1986. — ISBN 0-521-25654-2.
- William F. Reynolds. Hyperbolic geometry on a hyperboloid // American Mathematical Monthly. — 1993. — Вип. 100 (25 грудня).
- Scott Walter. The non-Euclidean style of Minkowskian relativity // The Symbolic Universe: Geometry and Physics. — Oxford University Press, 1999. — С. 91–127.
- Varićak V. On the Non-Euclidean Interpretation of the Theory of Relativity // Jahresbericht der Deutschen Mathematiker-Vereinigung. — 1912. — Т. 21 (25 грудня).
