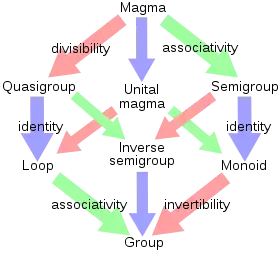
Напівгрупа

• Гомоморфізм між двома напівгрупами ${\displaystyle (S,\ast )}$ та ${\displaystyle (S^{\,\prime },\bullet )}$ є функція ${\displaystyle f:S\rightarrow S^{\prime }}$ така, що

${\displaystyle \forall x,y\in S:f(x\ast y)=f(x)\bullet f(y)}$.

• Якщо функція ${\displaystyle \ f}$ бієктивна, то це ізоморфізм напівгруп.

Якщо ${\displaystyle A,B\subset S}$, то позначають ${\displaystyle AB=\{ab:\;a\in A,b\in B\}}$

• Підмножина A напівгрупи S називається під-напівгрупою, якщо вона замкнута відносно групової операції. Тобто AA ⊆ A. Перетином під-напівгруп в S є під-напівгрупа в S.

• Якщо підмножина A непорожня та AS (SA) ⊆ A, то A називають правим (лівим) ідеалом. Якщо A є одночасно лівим і правим ідеалом, то його називають двохстороннім ідеалом, чи просто ідеалом.

• Перетином під-напівгруп( чи ідеалів) є під-напівгрупа (чи ідеал); з чого слідує, що напівгрупа або має мінімальну під-напівгрупу (чи ідеал) або не має їх зовсім.

• Якщо в комутативній напівгрупі є найменший ідеал, то він є групою.

Прикладом напівгрупи без найменшого ідеала є натуральні числа з операцією додавання.

• Натуральні числа ${\displaystyle \ \mathbb {N} }$ з операцією додавання є напівгрупою.
• Натуральні числа ${\displaystyle \ \mathbb {N} }$ з операцією множення є напівгрупою.
• Цілі числа ${\displaystyle \ \mathbb {Z} }$ з операцією множення є моноїдом.
• Ідеал кільця є напівгрупою відносно множення.
• Множина квадратних матриць розміру n з операцією множення є моноідом.

• Конкатенація

• Курош А. Г. Общая алгебра. — М. : Мир, 1970. — 162 с.(рос.)

• Кон П. Универсальная алгебра. — Москва : Мир, 1968. — 351 с.(рос.)