Розподіл Фреше
Розподіл Фреше, також відомий як обернений розподіл Вейбулла[2] [3], є окремим випадком узагальненого розподілу екстремального значення. Він має кумулятивну функцію розподілу
| Розподіл Фреше | |
|---|---|
 | |
|
Функція розподілу ймовірностей 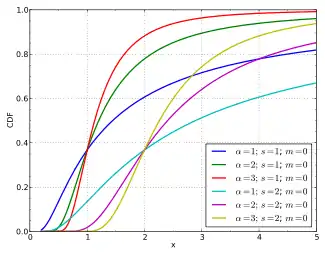 | |
| Параметри |
форми. (Необов'язкові, ще два параметри) масштаб (типове: ) зсув мінімуму (типове: ) |
| Носій функції | |
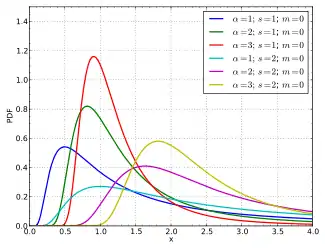
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Медіана | |
| Мода | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Ентропія | , де — стала Ейлера—Маскероні. |
| Твірна функція моментів (mgf) | Примітка: момент існує за умови[1] |
| Характеристична функція | [1] |
де α > 0 є параметром форми. Його можна узагальнити надаючи йому параметру розташування m (мінімум) і параметра масштабу s > 0 з кумулятивною функцією розподілу
Названий на честь Моріса Фреше , який написав статтю про цей розподіл у 1927 році, подальша робота була зроблена Фішером і Типпетом в 1928 і Гумбелем в 1958 році.
Характеристики
Єдиний параметр Фреше має стандартизований момент
(з ) визначений тільки при :
де це Гамма-функція.
Зокрема:
- Для математичне сподівання дорівнює
- Для в дисперсія становить
Квантиль порядку можна виразити оберненням функції розподілу,
- .
Зокрема, медіана - це:
Мода розподілу
Особливо для 3-параметричного розподілу Фреше, перший квартиль дорівнює , а третій квартиль
Також квантили для середнього та режиму:
Застосування
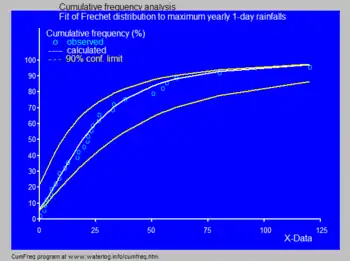
- В гідрології, розподіл Фреше застосовується для моделювання екстремальних явищ, таких як річна максимальна одноденна кількість опадів і річкового стоку[4]. Блакитний малюнок, зроблений на ПЗ CumFreq ілюструє моделювання розподілом Фреше річного денного максимуму опадів в Омані, на малюнку також показано 90% довірчий інтервал побудований на основі біноміального розподілу. Кумулятивні частоти спостережень кількости опадів представлені ґрафіком позицій в рамках сукупного частотного аналізу.
Однак, здебільшого в гідрології підгонку розподілу здійснюють через узагальнений розподіл екстремальних значень, що дозволяє уникнути припущення про відсутність нижньої межі розподілу (як того вимагає розподіл Фреше). [джерело?]
- Один тест для оцінки асимптотичної залежности чи незалежности багатовимірного розподілу полягає у перетворенні даних в стандартні відособлення Фреше за допомогою перетворення а потім відображення з картезіанських до псевдо-полярних координат . Значення відповідають граничним даним, для яких принаймні один компонент екстремальний, тоді як близькі до 1 або 0 означає, що тільки один компонент екстремальний.
Пов'язані розподіли
- Якщо (Рівномірний розподіл (безперервне)) тоді
- Якщо тоді
- Якщо і тоді
- Функція розподілу розподілу Фреше є розв'язком рівняння максимального постулату стабільности
- Якщо тоді обернена випадкова велчина має розподіл Вейбулла:
Властивості
- Розподіл Фреше є максимальним стабільним розподілом
- Фреше розподілена випадкова величина зі знаком мінус є мінімальним стабільним розподілом
Див. також
- Type-2 Gumbel distribution
- Fisher–Tippett–Gnedenko theorem
- CumFreq (application software for probability distributions including Fréchet)
Джерела
- Muraleedharan. G, C. Guedes Soares and Cláudia Lucas (2011). "Characteristic and Moment Generating Functions of Generalised Extreme Value Distribution (GEV)". In Linda. L. Wright (Ed.), Sea Level Rise, Coastal Engineering, Shorelines and Tides, Chapter 14, pp. 269–276. Nova Science Publishers. ISBN 978-1-61728-655-1 (англ.)
- Khan M.S.; Pasha G.R.; Pasha A.H. (February 2008). Theoretical Analysis of Inverse Weibull Distribution. WSEAS TRANSACTIONS on MATHEMATICS 7 (2). с. 30–38.
- de Gusmão, FelipeR.S. and Ortega, EdwinM.M. and Cordeiro, GaussM. (2011). The generalized inverse Weibull distribution. Statistical Papers 52 (3) (Springer-Verlag). с. 591–619. ISSN 0932-5026. doi:10.1007/s00362-009-0271-3.
- Coles, Stuart (2001). An Introduction to Statistical Modeling of Extreme Values,. Springer-Verlag. ISBN 1-85233-459-2.
Публікації
- Fréchet, M., (1927). "Sur la loi de probabilité de l'écart maximum." Ann. Soc. Polon. Math. 6, 93.
- Fisher, R.A., Tippett, L.H.C., (1928). "Limiting forms of the frequency distribution of the largest and smallest member of a sample." Proc. Cambridge Philosophical Society 24:180–190.
- Gumbel, E.J. (1958). "Statistics of Extremes." Columbia University Press, New York.
- Kotz, S.; Nadarajah, S. (2000) Extreme value distributions: theory and applications, World Scientific. ISBN 1-86094-224-5
