Синхронізація (нейробіологія)
У нейробіології, синхронізацією (від грец. συνχρόνος — одночасний) називають динамічний режим, який характеризується періодичною одночасною активацією певної популяції нейронів, або синхронізацію між локальними коливаннями двох або декількох популяцій нейронів.
Синхронізована активність у великих популяціях нейронів є головним механізмом утворення макроколивань, або так званих ритмів у головному мозку. Відомо, що ритми грають важливу роль у процесах передачі та обробки інформації у центральній нервовій системі (сон, пам'ять, увага, просторова навігація тощо), проте загальної теорії щодо точного призначення та принципів роботи ритмів наразі немає.
З іншого боку, надмірна локальна синхронізація в деяких мережах має патологічні прояви, такі як тремор у хворобі Паркінсона, епілептичні напади, а також деякі розлади вищої мозкової функції (шизофренія, аутизм, тощо).
Важлива роль синхронізації у процесах обробки інформації в мозку робить її дуже привабливої темою досліджень у медичній та обчислювальній нейронауці. Методи математичного моделювання синхронізації (часто запозичені з фізики) у поєднанні з доступністю обчислювальних потужностей створюють сприятливі умови для прогресу у напрямку більш глибокого та різнобічного розуміння цього явища.
Внаслідок того, що термін «синхронізація» є досить поширеним та часто використовується у різних галузях науки, його точне визначення може сильно варіювати в залежності від конкретної сфери застосування. У біологічному контексті, зручно розрізняти два види синхронізації[1]:
- локальна синхронізація (синхронізація активності окремої популяції нейронів що призводить до утворення макроколивань і може стає помітною в сигналі ЕЕГ)
- фазова синхронізація (синхронізація фази макроколивань між віддаленими ділянками мозку або групами нейронів)
У всіх секціях цієї статті, за винятком секції «Математичне моделювання», будемо використовувати саме вищенаведене визначення терміну «фазова синхронізація».
З іншого боку, в детальному математичному моделюванні локальної синхронізації прийнято використовувати термін «фазова синхронізація» в більш абстрактному сенсі. А саме, два або декілька осциляторів фазово синхронізовані, якщо відповідність їх фаз не змінюється з часом[2], або, у найбільш загальному визначенні, залежить відповідно до якось функції. При чому амплітуди коливань вищезгаданих осциляторів не обов'язково повинні бути однакові. Такими осциляторами можуть моделюватися як індивідуальні нейрони, так і мережі або великі популяції нейронів. У секції «Математичне моделювання» описано декілька типів синхронізації.
Роль у роботі ЦНС
Ритми ЕЕГ
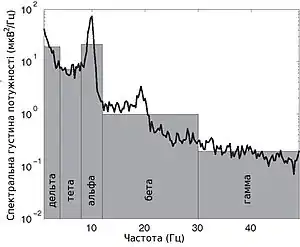
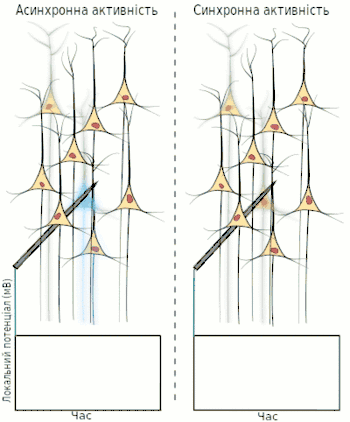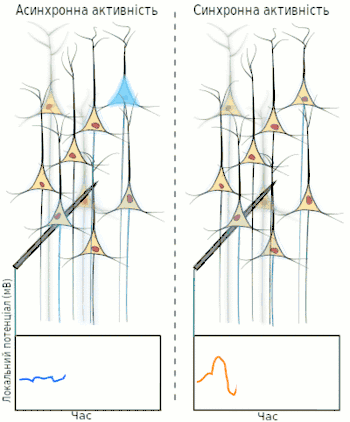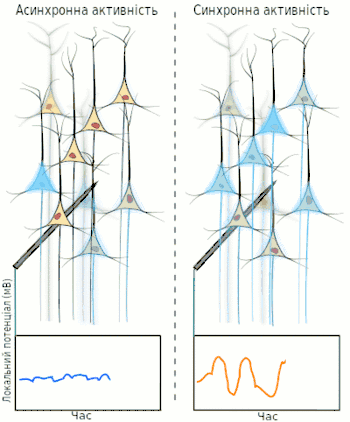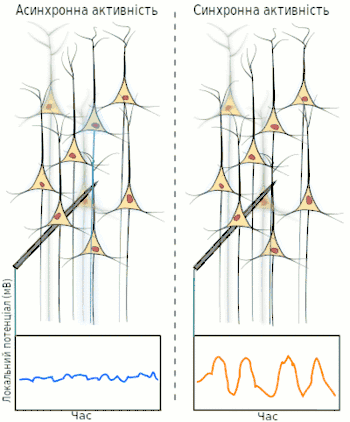
Електроенцефалографія (ЕЕГ) — один із ключових неінвазивних методів дослідження головного мозку, який характеризується високою часовою роздільною здатністю, але досить низькою просторовою роздільною здатністю, особливо порівнюючи з МРТ або інвазивними електродними методами. Через низьку просторову роздільну здатність (зазвичай не більше як 100 каналів), отриманий сигнал є результатом суперпозиції активності великих популяцій нейронів, а значить є зручним методом для знаходження та дослідження синхронізованих колективних режимів у мережах головного мозку. Синхронізація достатньо великої популяції нейронів зазвичай продукує глобальні коливання, які й записуються електродами електроенцефалографа.
У більшості випадків, сильна глобальна синхронізація великих популяцій (синхронізація типу I) притаманна стану бездіяльності або стану патологічному, адже динаміка повністю синхронізованої мережі не достатньо складна для ефективної обробки інформації. Під час нормальної ж роботи (окрім стану глибокого сну), невеликі локально-синхронізовані підмережі генерують коливання різних частот (синхронізація типу II), при цьому глобальна синхронізація зникає[4]. Таким чином, спектр ЕЕГ сигналу містить декілька важливих складових, які прийнято класифікувати за частотою, призначаючи кожному діапазонові грецьку літеру. У таблиці нижче наведено короткий опис кожного з ритмів, відповідно до традиційної системи класифікації, а також їх відповідні функції.
У наступних секціях більш детально розглянуто властивості та шляхи утворення деяких ритмів.
| Ритм | Частота (Гц) | Типова місце знаходження | Звичайні прояви | Графік |
|---|---|---|---|---|
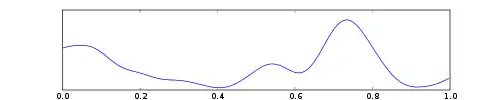
| Дельта | 0 — 4 | Фронтально у дорослих, постериально у дітей; Хвилі високої амплітуди |
|
|
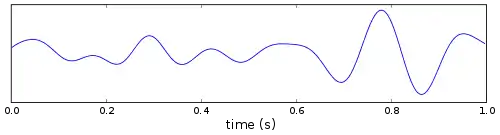
| Тета | 4 — 7 | Гіпокамп, кора |
|
|
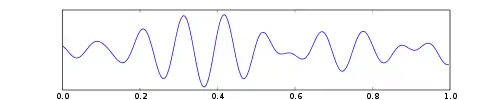
| Альфа | 8 — 12 | Постериальні ділянки голови, з обидвох сторін, але з більшою амплітудою на недомінантній стороні. Центральні локації (c3-c4) під час відпочинку |
|
|
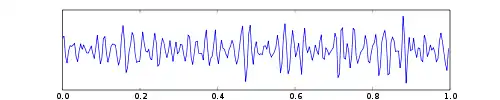
| Бета | 13 — 30 | Обидві сторони, найбільше фронтально; хвилі низької амплітуди |
|
|
| Гамма | 30 — 100+ | Соматосенсорна кора |
|
|
| Мю | 8 — 13 | Соматосенсорна та моторна кора |
|
|
Окрім вищезгаданих канонічних ритмів, сигнал ЕЕГ може також містити високочастотні компоненти, з частотою понад 400 Гц. У більшості випадків, такі компоненти мають дуже низьку енергію та часто нехтуються або сприймаються як шум. Однак нещодавні дослідження показали, що високочастотні коливання в сигналі ЕЕГ, які можна спостерігати в соматосенсорній корі головного мозку у відповідь на стимуляцію периферійного нерву, можуть бути результатом дуже точної синхронізації нейронних сплесків у відповідних мережах[9]. В експериментах з одночасним отриманням ЕЕГ та зовнішньоклітинного сигналу, було показано, що форма високочастотних компонентів сигналу ЕЕГ містить інформацію про часову структуру сплеску спайків індивідуальних нейронів. Таким чином, високочастотні ритми ЕЕГ можуть пролити світло на динаміку клітинного рівня, без втручання в біологічні тканини[9].
Центральні генератори впорядкованої активності
Синхронізована активність нейронів є базою для генерації періодичних моторних команд для ритмічних рухів. Ритмічні команди у свою чергу виробляються групою зв'язаних нейронів що формують мережу, яка називається центральний генератор впорядкованої активності (ЦГВА). При активації, такі нейронні мережі можуть генерувати складні ритмічні моторні команди, навіть за відсутності сигналів зворотнього зв'язку, що несуть інформацію про конкретні часові інтервали. Ходіння, плавання або дихання є прикладами роботи ЦГВА[10]. ЦВГА найбільш досліджені у нижчих тварин, таких як міногові, проте також існують свідчення про наявність ЦВГА у людей[11].
Пам'ять
Фазова синхронізація (ФС) коливань між різними зонами мозку має ряд важливих функцій, які є критичними для ефективної роботи пам'яті. Важливою функцією є покращення передачі інформації між віддаленими ділянками мозку під час ФС[1]. Оптимальна передача інформації може відбуватися завдяки ФС наступним чином: високий рівень локального потенціалу зазвичай свідчить про високий рівень активності в локальній популяції в даний момент часу. Одночасно, чутливість нейронів цієї популяції також підвищена, бо мембрани нейронів у середньому більш деполяризовані ніж коли локальний потенціал має низькі значення. Таким чином, якщо дві віддалені популяції нейронів мають синхронізовані колективні коливання, то момент підвищеної активності одної популяції збігатиметься з високою збудливістю іншої, забезпечуючи високу імовірність передачі інформації[12].
ФС також може сприяти підсиленню синаптичної пластичності. Синаптична пластичність що залежить від часу імпульсу (STDP) спричиняє довготривалу потенціацію синапсів, якщо приймаючий нейрон спрацьовує не більше як 10-20 мс після вхідного імпульсу. ФС може забезпечити достатньо вузькі інтервали спрацьовування нейронів між двома групами і таким чином збільшити або зменшити силу зв'язку між ними[1].
За поширеною системою класифікації, існують два основних види пам'яті:
У роботі короткочасної пам'яті, ФС спостерігається між префронтальною корою та скроневою долею мозку (на частоті θ-ритму) під час читання, запису та утримування короткочасних спогадів, а також між фронтальними та паріетальними зонами кори (на γ та β-частотах) під час утримування спогадів. Запис та читання візуальних об'єктів із декларативної пам'яті (тип довготривалої пам'яті) супроводжуються фазовою синхронізацією коливань між антериальними та постериальними зонами мозку на θ, γ, δ та β-частотах. Інші види синхронізації також беруть участь у репрезентації об'єктів у пам'яті[1].
Результати експериментів з одночасним записом електричної активності в гіпокампі та латеральній мигдалеподібній залозі свідчать про підсилення синхронізації на θ-частотах між цим ділянками після формації та під час дії умовного рефлексу страху[13].
Сон
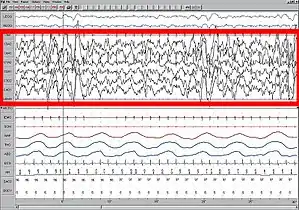
Під час глибокої фази сну, а також при деяких видах анестезії, на енцефалограмах зазвичай спостерігаються коливання низької частоти (0.3 — 1 Гц) та дельта коливання. Такі ритми часто асоціюються з відсутністю свідомості, а також часто використовуються як індикатор наявності свідомості у пацієнта під наркозом. На клітинному рівні, осциляції виглядають як періодична зміна станів активного спрацьовування нейронів та тиші, кожен з яких триває до одної секунди[14]. Одним із можливих механізмів генерації повільних коливань (до 1 Гц) є спільна робота відповідних мереж таламусу та неокортексу, наступним чином:
- активність нейронів у корі ініціює внутрішні осциляції в таламусі
- коливання в таламусі посилюють синхронізацію гальмівних інтернейронів
- активація гальмівних інтернейронів пригнічує активність нейронів кортексу і настає період тиші
- цикл повторюється
Інші механізми утворення низькочастотних коливань добре освітлено у роботі, на приклад, М. Тимофеєва[14].
При нормальних умовах, глибокий сон відіграє важливу роль у процесах консолідації пам'яті. Відповідно до популярної теорії, повільні колективні коливання регулюють ре-активацію та транспорт спогадів із гіпокампу до кортексу. Під час фази швидкого сну (підвищена тета-активність та локальна синаптична пластичність), ре-активовані спогади у кортексі закріплюються на синаптичному рівні, тобто відкладаються у довготривалу пам'ять[15] [16].
Увага
Увага — спрямованість психічної діяльності людини або тварини та її зосередженість у певний момент на об'єкти або явища, які мають певне значення при одночасному абстрагуванні від інших, у результаті чого вони відображаються повніше, чіткіше, глибше, ніж інші[17]. Під час концентрації уваги на конкретному об'єкті або його властивості, підвищується швидкість обробки інформації, зменшується час реакції, підвищується рівень точності, чутливості до невеликих змін у стимулі та сприйняття контрасту.
По перше, увага підсилює активність нейронів що репрезентують об'єкт уваги або певну характеристику (колір, орієнтація, тощо). Так, на приклад, нейрони зорової кори, рецептивне поле яких містить об'єкт уваги, сильніше синхронізовані з локальним потенціалом (на γ-частоті), ніж нейрони що реагують на інші об'єкти поза уваги. Такий спосіб селективного підсилення синхронізації імовірно є альтернативою підвищення частоти спрацьовування нейронів (вона зазвичай не змінюється в залежності від спрямування уваги)[18].
По друге, увага також регулює інформаційне сполучення між віддаленими частинами мозку, підсилюючи зв'язок між групами нейронів що несуть важливу для тварини інформацію. Багато досліджень приходять до виводу що таке підсилення зв'язку відбувається за рахунок селективної синхронізації між зонами кори[19].
Патологія
Під час нормальної роботи мозку, локальна та міжзонна синхронізація нейронної активності грають важливу роль у таких ключових процесах, як увага, пам'ять, моторика тощо. Однак важливим є також і певний баланс синхронізації та десинхронізації[20]. Надмірна або недостатня синхронізація може бути причиною багатьох патологічних процесів, у числі яких епілепсія, тремор, шизофренія, деменція, та деякі інші. Таким чином, важливим напрямком розвитку нейронауки є пошук ефективних шляхів знешкодження патологічної синхронізації, та розуміння принципів її утворення.
Епілепсія
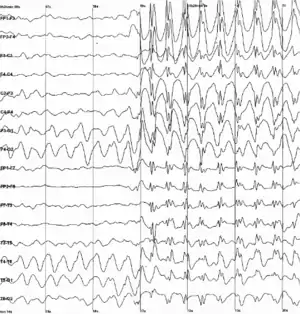
Епілепсія характеризується раптовим початком синхронізації у відносно великих нейронних мережах, внаслідок чого стає неможливою ефективна обробка інформації, що у свою чергу перешкоджає нормальній роботі мозку. Епілептичні напади можуть супроводжуватись короткочасною втратою свідомості або більш складними сенсорними та моторними проявами[20]. Найбільш проблематичним наслідком епілепсії є непередбачуваність нападів, внаслідок чого людям, що страждають епілепсією, може бути на законодавчому рівні заборонено керувати автотранспортом та виконувати деякі інші заняття, що вимагають постійної уваги.
Точні нейронні механізми епілептичної синхронізації наразі досконало не відомі. Проте застосування теорії динамічних систем до аналізу та моделювання сигналу що генерується такими мережами дає певні результати у напрямку розуміння феномену. Будь-яка нейронна мережа може бути описана як (нелінійна) динамічна система з одним або декількома атракторами. (Атрактор — це множина точок у фазовому просторі системи, до якої збігаються траєкторії системи. Іншими словами, це тип поведінки, до якого система повертається після невеликого відхилення в результаті зовнішнього втручання. Найпростішим прикладом атрактора є граничний цикл. На такому атракторі система починає описувати періодичні коливання). Згідно з однією з теорій, перехід від нормальної до епілептичної активності мережі може бути двох видів[21]:
- У результаті поступової деформації атрактора нормальної активності в атрактор активності епілептичної (через відповідну біфуркацію), внаслідок зміни параметрів системи (наприклад, зовнішньоклітинної концентрації іонів кальцію або магнію), або зовнішнього стимулу. Така модель відповідає типам нападів, коли зміна стану протікає поступово, у декілька фаз.
- Внаслідок різкого «перескакування» системи з одного нормального атрактора на атрактор синхронізованої активності, що було спричинено випадковою флуктуацією або зовнішнім стимулом (наприклад, спалахами світла). На відміну від першого випадку, тут система одночасно має два або кілька атракторів, включаючи нормальні й епілептичні (таку систему називають мультистабільною). У цьому випадку, в мозку здорової людини такі атрактори можуть бути розташовані далі один від одного, що унеможливлює випадковий перехід у стан епілептичного нападу).
У залежності від типу епілепсії, можуть бути застосовані різні підходи до моделювання динамічних процесів, що призводять до масової синхронізації нейронів[21] [22] [14].
Хвороба Паркінсона

Хвороба паркінсона — це рухове порушення, що повільно прогресує й супроводжується порушенням мови, скутістю, підвищенням тонусу м'язів, тремором та ригідністю м'язів, сповільненням рухів. Тремор, що характеризується ритмічними неконтрольованими рухами кінцівок, є дуже проблематичним симптомом, бо при певних умовах, унеможливлює виконання хворим багатьох повсякденних дій, таких як керування авто, утримування відкритої ємкості з рідиною, рукописання тощо.
Патологічний процес при цьому захворюванні характеризується деградацією дофамінергічних нейронів чорної речовини, що тягне за собою посилення активності та синхронізації нейронів у субталамічних ядрах (частина базальних ганглій) і призводить до надмірного гальмування таламо-кортикального зв'язку.
Наразі, точні механізми генерації тремору у пацієнтів із хворобою Паркінсона невідомі. Однак все більше даних кореляційного характеру свідчать про зв'язок між абнормально синхронізованою активністю в певних частинах мозку та м'язовим тремором[23] [24]. Так, відповідно до провідної гіпотези, тремор генерується групою нейронів у базальних ядрах, які працюють як центральні осцилятори та продукують періодичні імпульси певним групам м'язів. При чому важливим є як загальний рівень активності центральних осциляторів, так і рівень їх фазової синхронізації[23].
Когнітивні розлади
Шизофренія — це когнітивний розлад, головними симптомами якого є галюцинації, сильно спотворене сприйняття реальності, та загальна дезорганізація мислення та дій. Як і у випадку з багатьма складними ментальними захворюваннями, патофізіологія шизофренії досі залишається до кінця не відомою[25].
Як відомо, осциляторна активність мереж головного мозку пов'язана з такими важливими процесами як селективність до зовнішніх стимулів за допомогою уваги, пам'ять та свідомість. Через те, що симптоми шизофренії пов'язані саме з розладами вищезгаданих процесів, є підстави вважати, що абнормально низька β та γ-синхронізація, що спостерігається у хворих, є важливим фактором у патофізіології захворювання. Сучасні емпіричні дані свідчать про нелокальний та системний характер дисфункції головного мозку, що виникає при шизофренії, та може включати у себе розлад у динаміці нейронних мереж у префронтальних та тім'яних зонах, а також погіршення зв'язків між віддаленими зонами[25][26].
Аутизм, захворювання що пригнічує соціальну та комунікативну здібності пацієнтів, також було пов'язано зі зменшеною осиляторною активністю на γ-частотах. Хворі на аутизм страждають звуженим фокусом уваги та не здібні достатньо добре інтегрувати фрагменти інформації у єдине ціле, що може бути наслідком недостатньо ефективної передачі інформації між зонами мозку[25][26].
Фармацевтичні
Одним із поширених типів фармацевтичного пригнічення надмірної синхронізації, є використання різноманітних блокаторів іонних каналів, внаслідок чого зменшується збудливість цільових нейронів або ж пригнічуються синаптичні зв'язки. Наприклад, збільшення зовнішньоклітинної концентрації Mg2+ може припиняти синхронізовану коливальну активність у моделях епілепсії. З одного боку, це відбувається завдяки здатності іонів магнію блокувати NMDA-рецептори в синаптичних зв'язках між нейронами. З іншого боку, магній, та деякі інші 2 та 3-валентні іони (наприклад, Ca2+) можуть впливати на локальних заряд навколо натрієвих та калієвих потенціалчутливих каналів, знижуючи активаційний поріг та деякі динамічні характеристики нервової клітини[27] [28].
Фармацевтичних засоби також можуть діяти через зв'язування та деактивацію певних нейротрансмітерів.
Хірургічні
Майже третина пацієнтів з епілепсією не показують позитивної динаміки в результаті лікування антиепілептичними медикаментами[29]. Однак у деяких випадках (близько 7-8%), вдається достатньо точно локалізувати джерело абнормальної епілептичної синхронізації в мозку, яке видаляється за допомогою оперативного втручання. Сучасні хірургічні методи також дозволяють проведення операцій з видалення надмірно синхронізованих популяцій у глибокій сірій речовині (бліда куля, субталамічні ядра), для усунення симптомів багатьох моторних захворювань, включаючи хворобу Паркінсона[30].
Метод глибокої стимуляції мозку
Розвиток комп'ютерних технологій відкрив нову еру у лікуванні пацієнтів, які страждають на хворобу Паркінсона. Все частіше застосовується новий метод глибокої стимуляції мозку (Deep Brain Stimulation). Метод DBS полягає у використанні імпульсів електричного стимулятора, вбудованого поверхово в організм пацієнта. Через введений у мозок спеціальний електрод, імпульси подаються в базальні ганглії, зокрема, у субталамічні ядра, та виконують високочастотну стимуляцію груп нейронів, що призводить до помітного поліпшення у перебігу хвороби. Внаслідок суттєвого зменшення симптомів хвороби, пацієнти можуть повернутися до нормальної повсякденної діяльності та значно зменшити обсяг вживання ліків. Крім хвороби Паркінсона, показанням до операції є вроджені дистонії й есенціальний тремор[2]. Клінічні випробовування також тривають для застосування DBS у лікуванні депресії.
Не зважаючи на великий успіх DBS у лікуванні багатьох хвороб, технологія поки що знаходиться на ранньому етапі розвитку, та повна відмова від хірургічних втручань на користь DBS є темою дебатів[30].
Математичне моделювання
Мотивація
Методи математичного моделювання фізичних та хімічних процесів знайшли широке застосування в біофізиці та нейронауці. Починаючи від моделювання стохастичної динаміки окремих іонних каналів і закінчуючи мережами зі складною неоднорідною топологією та мільйонами нейронів, моделі допомагають науковцям зрозуміти механізми функціонування нервової системи на різних рівнях абстракції, а значить і знайти нові шляхи лікування відповідних захворювань, та розробляти більш розумні алгоритми та обчислювальні машини. Головним призначенням математичної моделі є усунення неважливих факторів з якогось процесу або спостереження, та кристалізація саме того мінімального набору механізмів, який є достатнім для пояснення даних, у конкретному контексті. Правильно побудована модель дозволяє тестувати цікаві гіпотези, та робити важливі передбачення щодо роботи тої чи іншої системи. У контексті синхронізації, моделювання дозволяє застосовувати аналітичні та чисельні методи для оцінки динамічних режимів мережі. Наприклад, біфуркаційний аналіз детальної моделі нейронної мережі може допомогти визначити максимально допустимі значення фізіологічних параметрів, що не призведуть до переходу мережі у патологічно синхронізований режим.
Моделі біологічного нейрона
Біологічний нейрон можна моделювати на різних рівнях абстракції, але суть багатьох моделей полягає у виділенні квазіперіодичних властивостей його динаміки, тобто зображення нейрона як осцилятора певного рівня складності.
Модель Курамото
Модель з'єднаних осциляторів Курамото[31] — одна з найбільш абстрактних моделей призначених для дослідження синхронізації та коливань у нейронних мережах (осцилятори мають лише одну степінь свободи — фазу коливань, ігноруючи амплітуду)[32]. Взаємодії між такими осциляторами описуються простою алгебраїчною формою (такою як синус), та колективно генерують певну картину глобальної активності. Модель Курамото та її розширення (такі як наприклад додавання можливості формувати зв'язки різної сили) широко використовується для вивчення коливальних процесів у мозку[33]. Зокрема, її зручно використовувати для вивчення механізмів початку синхронізації в групі пов'язаних нейронів.
У найпростішому вигляді, фаза () кожного з N нейронів задається наступним чином:
де це частота коливання i-того осцилятору, та — сила з'єднання та елемент матриці з'єднань відповідно.
Завдяки простоті визначення, можна відносно швидко симулювати динаміку великих популяцій таких нейронів, а також знаходити аналітичні рішення в певних випадках.
Спайкові моделі
Спайкові моделі нейронів використовуються у випадках, коли не можна обмежитись лише фазовою або частотною абстракцією нейрона, тобто коли необхідно враховувати амплітуду коливань, та/або інші, більш детальні аспекти роботи біологічного нейрона. Характерною властивістю спайкових моделей є здатність генерувати активність, наближену до потенціалу дії (спайку). Такі мережі є дуже корисними, коли необхідно зробити передбачення щодо значень певних біологічних параметрів, бо в їх математичне визначення часто включені аналоги біологічних параметрів (наприклад, динаміка іонних каналів або концентрація певних речовин у зовнішньоклітинному середовищі). Однак головним недоліком таких моделей є складність та нелінійність їх математичного визначення, що обмежує можливості аналітичних розв'язків та вимагає суттєвих затрат комп'ютерного часу для рішень чисельних.
Зазвичай один такий нейрон визначається системою нелінійних диференційних рівнянь. В обчислювальній нейронауці найбільш популярними є наступні моделі:
- експоненційна модель «інтегрувати і спрацювати» (AdEx)[34]. Є найпростішою моделлю що здатна продукувати всі основні динамічні режими біологічного нейрону, такі як одноразове спрацьовування, регулярне спрацьовування у відповідь на стимуляцію постійним струмом, пачкова активність тощо. Широко використовується у дослідженнях синхронізації у великих гетерогенних популяціях нейронів. Описується системою з двох диференційних рівнянь.
- Модель Хіндмарша-Роуза (HR) — одна з найпростіших неперервних моделей, що здатні генерувати пачкову, а також хаотичну активності. Описується системою з трьох диференційних рівнянь[35].
- Модель Годжкіна-Гакслі (HH) та похідні — сімейство детальних біологічно-реалістичних моделей нейронів, що включають у себе кінетику натрієвих, калієвих, кальцієвих та інших іонних каналів. Різні модифікації здатні дуже точно імітувати форму потенціалу дії справжніх нейронів. Система зазвичай описується щонайменш чотирма нелінійними диференційними рівняннями. Не зважаючи на складність математичного визначення, HH-подібні моделі успішно використовуються для досліджень ефектів синхронізації у великих популяціях нейронів[36].
Види синхронізації осциляторів
Існує велика кількість різних визначень явища синхронізації, які можуть бути застосовані в тому чи іншому контексті. Відзначимо деякі основні види синхронізації
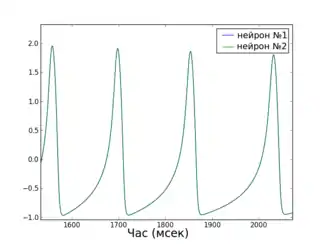
- Повна синхронізація — найпростіший, з математичної точки зору, тип синхронізації, яких характеризується повною збіжністю відповідних змінних всіх нейронів у мережі. Наприклад, якщо i-тий нейрон описується вектором змінних , то кажуть що мережа з N нейронів повністю синхронізована, якщо її стан відповідає рівнянню . Стан повної синхронізації може бути досягнутий тільки у мережі з ідентичними нейронами.
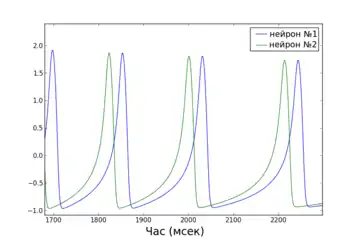
- Фазова синхронізація накладає певні обмеження на фазові відношення між осциляторами, ігноруючи відношення амплітуд. Якщо у системи можна визначити поняття фази, то фазова синхронізація мережі таких осциляторів означає, що різниця фаз між елементами мережі повинна або взагалі не змінюватись із часом, або знаходитись у певних скінченних границях[37]. Такий підхід дозволяє досліджувати синхронізацію мереж з осциляторами, параметри яких можуть відрізнятися.
- Узагальнена синхронізація. Як фазова, тільки відношення між фазами повинні описуватися певною функцією.
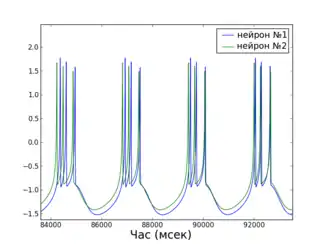
- Пачкова синхронізація — синхронізація нейронів під час пачкової активності. Така синхронізація не вимагає точного збігу моментів спайків нейронів, але вимагає синхронізованого спрацьовування пачок спайків (ритмічних, обмежених у часі сплесків активності з генерацією декількох потенціалів дії)[38].
Глобальна функція стабільності синхронізованого стану

Простота математичного визначення стану повної синхронізації робить можливим застосування цікавих аналітичних методів для дослідження цього виду синхронізації. Глобальна функція стабільності синхронізованого стану (Master Stability Function, MSF), на приклад, дозволяє визначати стабільність стану повної синхронізації для мережі ідентичних нейронів[39]. Іншими словами, розрахувавши MSF для мережі потрібних моделей нейронів, можна з точністю сказати чи існують такі топології з'єднання нейронів, при яких дана мережа буде здатна синхронізуватися (тобто буде мати стабільний стан повної синхронізації). Краса методу полягає у тому, що MSF треба розраховувати лише один раз для кожного конкретного типу моделі та набору параметрів, а з результату можна робити висновки про стабільність синхронізованого стану для будь-якої кількості нейронів та будь-якої топології (при дотриманні умови однакової сумарної сили вхідного сигналу для нейронів).
Основний процес аналізу синхронізації системи за допомогою MSF можна розбити на кілька кроків. Розглянемо мережу ідентичних зв'язаних нейронів, кожен з яких описується певною системою диф. рівнянь (наприклад, Модель Ходжкіна-Хакслі). Тоді мережу з N нейронів можна записати у такому вигляді:
-
()
де ; це D-вимірний вектор змінних i-того нейрона (вектор стану); та — векторні поля що описують відповідно (нелінійну) внутрішню динаміку (звичайне мат. визначення нейрону) та функцію зв'язку між елементами; елемент матриці що містить сили синаптичних зв'язків між нейронами.
Отож, загальна розмірність фазового простору всієї мережі дорівнюватиме . Часто потрібно аналізувати мережу з великою кількістю нейронів (), і тоді прямий аналіз стабільності синхронізованого стану мережі (за допомогою, наприклад, експонент Ляпунова) стає занадто громіздкою обчислювальною задачею. З іншого боку, відповідно до формалізму MSF, для визначення стабільності синхронізованого стану вищенаведеної системи, достатньо розрахувати експоненти Ляпунова для набагато меншої, лінеаризованої D-вимірної системи, що задається рівнянням (припустимо, що матриця зв'язків має виключно реальні власні числа):
-
()
де — якобіан векторного поля, розрахований уздовж синхронізованого рішення (під синхронізованим рішенням тут мається на увазі чисельне рішення рівняння одного нейрона, з'єднаного із самим собою), а — спеціальний скалярний параметр.
Опустивши деталі, маємо наступний алгоритм:
- Розрахувати максимальну експоненту Ляпунова () невеликої лінійної системи (2), для потрібного діапазону параметру ;
- Побудувати графік залежності від параметру та визначити діапазони параметру де має від'ємний знак;
- Знайти власні числа матриці зв'язків
- Якщо всі власні числа матриці зв'язків (за винятком того, яке дорівнює рядковій сумі матриці, див.[39]) попадають у діапазон , що відповідає негативній — мережа має стабільний стан повної синхронізації
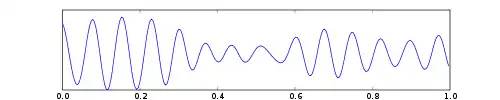
Приклад графіку MSF для HR нейронів, а також відео процесу повної синхронізації невеликої мережі (відповідно до передбачення MSF) наведено праворуч.
Джерела
- Juergen Fell & Nikolai Axmacher (February 2011). The role of phase synchronization in memory processes. Nature reviews. Neuroscience 12 (2): 105–118. PMID 21248789. doi:10.1038/nrn2979.
- Фазова синхронізація. Архів оригіналу за 10 січня 2014.
- S. J. van Albada & P. A. Robinson (2013). Relationships between Electroencephalographic Spectral Peaks Across Frequency Bands. Frontiers in human neuroscience 7: 56. PMID 23483663. doi:10.3389/fnhum.2013.00056.
- W. Klimesch (November 1996). Memory processes, brain oscillations and EEG synchronization. International journal of psychophysiology : official journal of the International Organization of Psychophysiology 24 (1-2): 61–100. PMID 8978436.
- Kirmizi-Alsan, Elif; Bayraktaroglu, Zubeyir; Gurvit, Hakan; Keskin, Yasemin H.; Emre, Murat; Demiralp, Tamer (2006). Comparative analysis of event-related potentials during Go/NoGo and CPT: Decomposition of electrophysiological markers of response inhibition and sustained attention. Brain Research 1104 (1): 114–28. PMID 16824492. doi:10.1016/j.brainres.2006.03.010.
- Kisley, Michael A.; Cornwell, Zoe M. (2006). Gamma and beta neural activity evoked during a sensory gating paradigm: Effects of auditory, somatosensory and cross-modal stimulation. Clinical Neurophysiology 117 (11): 2549–63. PMC 1773003. PMID 17008125. doi:10.1016/j.clinph.2006.08.003.
- Kanayama, Noriaki; Sato, Atsushi; Ohira, Hideki (2007). Crossmodal effect with rubber hand illusion and gamma-band activity. Psychophysiology 44 (3): 392–402. PMID 17371495. doi:10.1111/j.1469-8986.2007.00511.x.
- Gastaut, H (1952). Electrocorticographic study of the reactivity of rolandic rhythm. Revue neurologique 87 (2): 176–82. PMID 13014777.
- Bartosz Telenczuk, Stuart N. Baker, Andreas V. M. Herz & Gabriel Curio (June 2011). High-frequency EEG covaries with spike burst patterns detected in cortical neurons. Journal of neurophysiology 105 (6): 2951–2959. PMID 21490283. doi:10.1152/jn.00327.2010.
- Marder E, Bucher D (2001). Central pattern generators and the control of rhythmic movements. Curr Biol 11: R986–R996. doi:10.1016/S0960-9822(01)00581-4.
- Dimitrijevic MR, Gerasimenko Y, Pinter MM (1998). Evidence for a spinal central pattern generator in humans. Ann NY Acad Sci 860: 360–376. PMID 9928325. doi:10.1111/j.1749-6632.1998.tb09062.x.
- Womelsdorf, T.; Schoffelen, J.-M.; Oostenveld, R.; Singer, W.; Desimone, R.; Engel, A. K.; Fries, P. (2007). Modulation of Neuronal Interactions Through Neuronal Synchronization. Science 316 (5831): 1609–1612. ISSN 0036-8075. doi:10.1126/science.1139597.
- Thomas Seidenbecher, T. Rao Laxmi, Oliver Stork & Hans-Christian Pape (August 2003). Amygdalar and hippocampal theta rhythm synchronization during fear memory retrieval. Science (New York, N.Y.) 301 (5634): 846–850. PMID 12907806. doi:10.1126/science.1085818.
- Timofeev, I.; Bazhenov, M.; Seigneur, J. (2012). У Noebels, J. L. Neuronal Synchronization and Thalamocortical Rhythms in Sleep, Wake and Epilepsy. History of the Second World War, United Kingdom Military Series. National Center for Biotechnology Information (US).
- Diekelmann, Susanne; Born, Jan (2010). The memory function of sleep. Nature Reviews Neuroscience. ISSN 1471-003X. doi:10.1038/nrn2762.
- Diekelmann, Susanne; Born, Jan (2010). Slow-wave sleep takes the leading role in memory reorganization. Nature Reviews Neuroscience 11 (3): 218–218. ISSN 1471-003X. doi:10.1038/nrn2762-c2.
- Українська психологічна термінологія: словник-довідник. За ред. М.-Л. А. Чепи. — К.: ДП «Інформаційно-аналітичне агентство», 2010. ISBN 978-617-571-040-0.
- Fries, P. (2001). Modulation of Oscillatory Neuronal Synchronization by Selective Visual Attention. Science 291 (5508): 1560–1563. ISSN 00368075. doi:10.1126/science.1055465.
- Thilo Womelsdorf & Pascal Fries (April 2007). The role of neuronal synchronization in selective attention. Current opinion in neurobiology 17 (2): 154–160. PMID 17306527. doi:10.1016/j.conb.2007.02.002.
- Alfons Schnitzler & Joachim Gross (April 2005). Normal and pathological oscillatory communication in the brain. Nature reviews. Neuroscience 6 (4): 285–296. PMID 15803160. doi:10.1038/nrn1650.
- Fernando H. Lopes da Silva, Wouter Blanes, Stiliyan N. Kalitzin, Jaime Parra, Piotr Suffczynski & Demetrios N. Velis (May 2003). Dynamical diseases of brain systems: different routes to epileptic seizures. IEEE transactions on bio-medical engineering 50 (5): 540–548. PMID 12769430. doi:10.1109/TBME.2003.810703.
- Perez Velazquez, Jose L; Cortez, Miguel A; Snead, O.Carter; Wennberg, Richard (2003). Dynamical regimes underlying epileptiform events: role of instabilities and bifurcations in brain activity. Physica D: Nonlinear Phenomena 186 (3-4): 205–220. ISSN 01672789. doi:10.1016/j.physd.2003.07.002.
- Bartolić, Andrej; Pirtošek, Zvezdan; Rozman, Janez; Ribarič, Samo (2010). Tremor amplitude and tremor frequency variability in Parkinson’s disease is dependent on activity and synchronisation of central oscillators in basal ganglia. Medical Hypotheses 74 (2): 362–365. ISSN 03069877. doi:10.1016/j.mehy.2009.06.057.
- R. Levy, W. D. Hutchison, A. M. Lozano & J. O. Dostrovsky (October 2000). High-frequency synchronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor. The Journal of neuroscience : the official journal of the Society for Neuroscience 20 (20): 7766–7775. PMID 11027240.
- Peter J. Uhlhaas & Wolf Singer (February 2010). Abnormal neural oscillations and synchrony in schizophrenia. Nature reviews. Neuroscience 11 (2): 100–113. PMID 20087360. doi:10.1038/nrn2774.
- Wang, X.-J. (2010). Neurophysiological and Computational Principles of Cortical Rhythms in Cognition. Physiological Reviews 90 (3): 1195–1268. ISSN 0031-9333. doi:10.1152/physrev.00035.2008.
- B. Frankenhaeuser & A. L. Hodgkin (July 1957). The action of calcium on the electrical properties of squid axons. The Journal of physiology 137 (2): 218–244. PMID 13449874.
- Dmytro Isaev, Gleb Ivanchick, Volodymyr Khmyz, Elena Isaeva, Alina Savrasova, Oleg Krishtal, Gregory L. Holmes & Oleksandr Maximyuk (January 2012). Surface charge impact in low-magnesium model of seizure in rat hippocampus. Journal of neurophysiology 107 (1): 417–423. PMID 22031777. doi:10.1152/jn.00574.2011.
- Klaus Lehnertz, Stephan Bialonski, Marie-Therese Horstmann, Dieter Krug, Alexander Rothkegel, Matthaus Staniek & Tobias Wagner (September 2009). Synchronization phenomena in human epileptic brain networks. Journal of neuroscience methods 183 (1): 42–48. PMID 19481573. doi:10.1016/j.jneumeth.2009.05.015.
- Michael S. Okun & Jerrold L. Vitek (April 2004). Lesion therapy for Parkinson's disease and other movement disorders: update and controversies. Movement disorders : official journal of the Movement Disorder Society 19 (4): 375–389. PMID 15077235. doi:10.1002/mds.20037.
- Kuramoto Y (1984). Chemical Oscillations, Waves, and Turbulence. Dover Publications.
- Ermentrout B (1994). An introduction to neural oscillators. In F Ventriglia (ed.), Neural Modeling and Neural Networks: 79–110.
- Breakspear M, Heitmann S, Daffertshofer A (2010). 190. Generative models of cortical oscillations: Neurobiological implications of the Kuramoto model. Front Hum Neurosc 4. doi:10.3389/fnhum.2010.00190.
- Brette, R. (2005). Adaptive Exponential Integrate-and-Fire Model as an Effective Description of Neuronal Activity. Journal of Neurophysiology 94 (5): 3637–3642. ISSN 0022-3077. doi:10.1152/jn.00686.2005.
- Hindmarsh, J. L.; Rose, R. M. (1984). A Model of Neuronal Bursting Using Three Coupled First Order Differential Equations. Proceedings of the Royal Society B: Biological Sciences 221 (1222): 87–102. ISSN 0962-8452. doi:10.1098/rspb.1984.0024.
- Golomb, D. (2005). Persistent Synchronized Bursting Activity in Cortical Tissues With Low Magnesium Concentration: A Modeling Study. Journal of Neurophysiology 95 (2): 1049–1067. ISSN 0022-3077. doi:10.1152/jn.00932.2005.
- Brown, Reggie; Kocarev, Ljupčo (2000). A unifying definition of synchronization for dynamical systems. Chaos: An Interdisciplinary Journal of Nonlinear Science 10 (2): 344. ISSN 10541500. doi:10.1063/1.166500.
- Rubin, Jonathan (2007). Burst synchronization. Scholarpedia 2 (10): 1666. ISSN 1941-6016. doi:10.4249/scholarpedia.1666.
- Pecora, Louis M.; Carroll, Thomas L. (1998). Master Stability Functions for Synchronized Coupled Systems. Physical Review Letters 80 (10): 2109–2112. ISSN 0031-9007. doi:10.1103/PhysRevLett.80.2109.
|
|
Ця стаття належить до добрих статей української Вікіпедії. |