Бета-біноміальний розподіл
У теорії ймовірностей і статистиці, бета-біноміальний розподіл являє собою сімейство дискретних імовірнісних розподілів на скінченному носії невід'ємних цілих чисел, що виникає коли ймовірність успіху в кожному з фіксованих чи відомого числа випробувань Бернуллі або невідома, або є випадковою. Бета-біноміальний розподіл — це біноміальний розподіл, у якому ймовірність успіху в кожному з n випробувань не є фіксованою, а є випадковою реалізацією бета-розподіленої випадкової величини. Розподіл часто використовується в байєсівській статистиці, емпіричних методах Байєса та класичній статистиці для виявлення наддисперсії в біноміально розподілених даних.
| Бета-біноміальний розподіл | |
|---|---|
|
Функція ймовірностей  | |
|
Функція розподілу ймовірностей 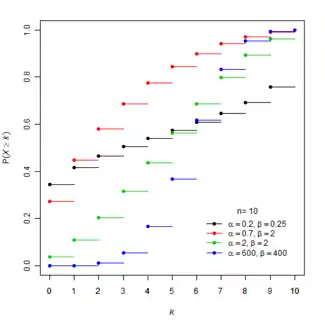 | |
| Параметри |
n ∈ N0 — число випробувань (дійсне) (дійсне) |
| Носій функції | k ∈ { 0, …, n } |
| Розподіл імовірностей |
де — Бета-функція |
| Функція розподілу ймовірностей (cdf) |
де 3F2(a;b;x) — узагальнена гіпергеометрична функція |
| Середнє | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | See text |
| Твірна функція моментів (mgf) | де — гіпергеометрична функція |
| Характеристична функція |
|
| Генератриса (pgf) |
|
Він зводиться до звичайного розподілу Бернуллі, коли n=1. Для α=β=1, це дискретний рівномірний розподіл від 0 до n. Він також як завгодно добре наближує біноміальний розподіл для великих α і β . Аналогічно, зводиться негативного біноміального розподілу при великими значеннями β і n. Бета-біноміальний є одновимірною версією мультиноміального розподілу Діріхле, оскільки біноміальний та бета-розподіл є одновимірними версіями мультиноміального та розподілу Діріхле відповідно.
Особливий випадок, коли α і β є цілими числами, також відомий як негативний гіпергеометричний розподіл.
Мотивація та виведення
Як складений розподіл
Бета-розподіл — це спряжений розподіл біноміального розподілу . Цей факт дозволяє аналітично вивести складений розподіл, якщо вважати параметр у біноміальному розподілі як випадкову реалізацію бета-розподіленої випадкової величини. А саме, якщо
тоді
де Bin( n, p ) означає біноміальний розподіл, а де p — випадкова величина з бета-розподілом.
тоді складений розподіл визначається як
Використовуючи властивості бета-функції, вираз можна переписати
Бета-біноміал як модель урни
Бета-біноміальний розподіл також можна пояснити за допомогою моделі урн для цілих додатних значень α і β, відомої як модель урни Полі. Зокрема, уявіть собі урну, що містить α червоних кульок та β чорних кульок, звідки їх виймають навмання. Якщо дістали червону кульку, то до урни повертають дві червоні кульки. Аналогічно з чорними кульками, якщо дістають чорну кулю, то натомість в урну повертають дві чорні. Якщо експеримент повторити n разів, то ймовірність отримати k червоних куль буде мати бета-біноміальний розподіл з параметрами n, α і β .
Якщо випадкові випробування здійснюються з простою заміною (повертають тільки одну, ту що щойно дістали, кульку), то маємо справу з біноміальним розподілом, а якщо експеримент здійснюються без заміни, то спостерігаємо реалізацію гіпергеометрично розподіленої випадкової величини.
Моменти та властивості
Перші три моменти
Ексцес задається формулою
Позначимо , тоді середнє можна записати як
і дисперсія як
де . Параметр відомий як кореляція «всередині класу» або «внутрішньокластерна» кореляція. Саме ця позитивна кореляція призводить до надмірної дисперсії.
Точкові оцінки
Метод моментів
Методом моментів можна отримати оцінки, а саме запишемо перший і другий моменти бета-біноміального розподілу
і прирівняємо ці нецентральні моменти до першого та другого нецентрального моменту вибірки відповідно
розв’яжемо для α і β і отримуємо
Ці оцінки можуть виглядати безглуздо негативними, що є доказом того, що дані є або нерозподілені зовсім або розподілені недостатньо у порівнянні до біноміального розподілу. У цьому випадку біноміальний розподіл і гіпергеометричний розподіл є альтернативними кандидатами відповідно.
Оцінка максимальної ймовірності
Хоч формула оцінки методом максимальної правдоподібності є непрактичною, враховуючи, що щільність складається із звичних функцій (гамма-функції та/або бета-функції), їх можна легко знайти за допомогою прямої чисельної оптимізації. Оцінки максимальної правдоподібності на основі емпіричних даних можуть бути обчислені за допомогою загальних методів підгонки мультиноміальних розподілів Полі, методи для яких описані в (Minka 2003). Пакет R VGAM через функцію vglm, використовуючи метод максимальної правдоподібності, полегшує оцінку УЛМ моделей з результатами, розподіленими за бета-біноміальним розподілом. Немає явної вимоги аби n було фіксованим впродовж спостережень.
Приклад
Наведені нижче дані показують кількість дітей чоловічої статі серед перших 12 дітей у 6115 сім'ях з 13-ма дітьми, взятих із лікарняних карт Саксонії 19 століття (Sokal and Rohlf, с.59 від Ліндсі). 13-ту дитину ігнорують, щоб пом’якшити ефект від того, що родина перестала пробувати завести дитину за умови досягнення бажаної статі.
| Хлопчики | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Родини | 3 | 24 | 104 | 286 | 670 | 1033 | 1343 | 1112 | 829 | 478 | 181 | 45 | 7 |
Перші два емпіричні моменти
тому оцінка методом моментів
Оцінка методом максимальної ймовірності можна вирахувати чисельними методами
і максимальна логарифмічна правдоподібність
звідси знаходимо AIC
AIC для конкуруючої біноміальної моделі є AIC = 25070.34, таким чином, бачимо, що бета-біноміальна модель забезпечує кращу відповідність даним, тобто присутні докази надмірної дисперсії. Трайверс і Віллард висувають теоретичне обгрунтування гетерогенності (також відомої як «розривність») у гендерній схильності нащадків ссавців (тобто надмірна дисперсність).
Краща припасовка особливо добре помітна в хвостах
| Хлопці | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Спостережувані родини | 3 | 24 | 104 | 286 | 670 | 1033 | 1343 | 1112 | 829 | 478 | 181 | 45 | 7 |
| Очікуваний число (бета-біноміальний) | 2.3 | 22.6 | 104.8 | 310.9 | 655.7 | 1036.2 | 1257.9 | 1182.1 | 853.6 | 461.9 | 177,9 | 43.8 | 5.2 |
| Очікуваний число ( біноміальний p = 0,519215) | 0.9 | 12.1 | 71.8 | 258.5 | 628.1 | 1085.2 | 1367.3 | 1265.6 | 854.2 | 410,0 | 132.8 | 26.1 | 2.3 |
Подальші байєсівські міркування
Зручно перепараметризувати розподіли так, щоб очікуване середнє значення апріорного розподілу було одним параметром, нехай
де
таким чином
Апостеріорний розподіл ρ ( θ | k ) також є бета-розподілом:
І
тоді як граничний розподіл m ( k | μ, M ) визначається як
Підставляючи назад M і μ, в термінах і , отримаємо:
який і є очікуваним бета-біноміальним розподілом з параметрами і .
Ми також можемо використати метод повторних матсподівань, щоб знайти очікуване значення граничних моментів. Запишемо нашу модель як двоступеневу модель складної вибірки. Нехай k i — кількість успіхів із n i спроб для події i :
Можемо знайти покрокові оцінки моментів для середнього та дисперсії, використовуючи моменти для розподілів у двокроковій моделі:
(Тут ми використовували закон повного матсподівання і закон повної дисперсії.)
Знайдемо точкові оцінки і . Розрахункове середнє розраховується з вибірки
Оцінку гіперпараметра M можна обчислити використовуючи оцінки моментів для дисперсії з двокрокової моделі:
І розв'яжемо для М:
де
Оскільки тепер ми маємо оцінки параметрів, і , для основного розподілу можемо знайти точкову оцінку для ймовірності успіху події i . Її можна обчислити як середнє зважене значення оцінки події і . Враховуючи наші точкові оцінки для апріора, можна підставити їхні значення, щоб знайти точкову оцінку для апостеріору
Фактори усадки
Можемо записати апостеріорну оцінку як середньозважене:
де називається коефіцієнтом усадки .
Пов'язані розподіли
Див. також
- Мультиноміальний розподіл Діріхле
Посилання
- Minka, Thomas P. (2003). Estimating a Dirichlet distribution. Microsoft Technical Report.
Зовнішні посилання
- Using the Beta-binomial distribution to assess performance of a biometric identification device
- Fastfit contains Matlab code for fitting Beta-Binomial distributions (in the form of two-dimensional Pólya distributions) to data.
- Interactive graphic: Univariate Distribution Relationships
- Beta-binomial functions in VGAM R package
- Beta-binomial distribution in Sandia National Labs Cognitive Foundry Java library
