Об'єм

Об'є́м — місткість геометричного тіла, тобто частини простору, обмеженої однією або декількома замкнутими поверхнями. Об'єм виражається числом кубічних одиниць, що поміщаються в певній ємкості.

Мірна чашка може бути використана для вимірювання об'єму рідин

Об'єм це величина, що визначає кількість тривимірного простору в середині замкнутої поверхні, наприклад, це простір, який заповнює або містить в собі речовина (тверде тіло, рідина, газ, або плазма) або фігура.

Кількість тривимірного простору в середині замкнутої поверхні, наприклад, це простір, який заповнює або містить у собі речовина (тверде тіло, рідина, газ, або плазма) або фігура. Прийняті одиниці вимірювання в системі SI та частинні від неї — кубічний метр, кубічний сантиметр, літр (кубічний дециметр) тощо. Позасистемні — галон, барель, бушель.

Тривимірні математичні фігури також мають об'єм. Об'єми деяких простих фігур, як-от правильні прямолінійні або округлі можна легко розрахувати за допомогою арифметичних формул. Об'єми складних форм можуть розраховуватися за допомогою інтегрального числення, при умові що існує формула для визначення межі, що обмежує фігуру. Там, де існують варіацій у формі й об'ємі, як, наприклад, різниця у відмінності людського тіла, об'єм може розраховуватися за допомогою методів у тривимірному просторі, як-от індекс об'єму тіла. Одновимірні фігури (як-от прямі) і двовимірні фігури (як-от квадрати) мають нульове значення об'єму в тривимірному просторі.

Об'єм твердого тіла (правильної форми чи довільної) можна визначити кількістю витісненої рідини. Цей підхід також можна використовувати для визначення об'єму газу. Загальний об'єм двох поєднаних між собою речовин, як правило

Одиниці вимірювання

Будь-яка міра довжини утворює відповідну міру об'єму: об'єм кубу сторони якого мають задану довжину. Наприклад, кубічний сантиметр (см³) це об'єм кубу, довжина сторін якого становить один сантиметр (1 см).

У Міжнародній системі одиниць (SI) одиницею вимірювання об'єму є кубічний метр (м³). Метрична система також містить таку одиницю як літр (л) для вимірювання об'єму, що дорівнює об'єму 10-сантиметрового куба. Таким чином

1 літр = (10 см)³ = 1000 кубічних сантиметрів = 0.001 кубічного метра,

а отже

1 кубічний метр = 1000 літрів.

Невелику кількість рідини часто вимірюють в мілілітрах, де

1 мілілітр = 0.001 літрів = 1 кубічний сантиметр.

Об'єм у теорії числення

У теорії числення об'єм області D в просторі R³ задається потрійним інтегралом константної функції $f(x,y,z)=1$ і зазвичай записується наступним чином:

\iiint \limits _{D}1\,dx\,dy\,dz.

Об'ємний інтеграл в циліндричній системі координат буде наступним

\iiint \limits _{D}r\,dr\,d\theta \,dz,

а об'ємний інтеграл в сферичних координатах (що використовує позначення для кутів $\theta$ в якості азимуту і $\phi$ , що відміряється від полярної осі;) має форму

\iiint \limits _{D}\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi .

Формули для обчислення об'єму

Загальні формули об'ємів:
Тіло	Формула	Величини
Куб	$s^{3}=s\cdot s\cdot s$	s = ребро куба
Прямокутна призма	$l\cdot w\cdot h$	l = довжина, w = ширина, h = висота
Трикутна призма	${\frac {1}{2}}bhl$	b = довжина основи трикутника, h = висота трикутника, l = висота призми або відстань між основами трикутника
Циліндр	$\pi r^{2}\cdot h$	r = радіус основи циліндра, h = висота
Будь-яка призма, що має постійну площу перетину поперек всієї висоти:	$A\cdot h$	A = площа основи, h = висота
Куля	${\frac {4}{3}}\pi r^{3}$	r = радіус кулі
Еліпсоїд	${\frac {4}{3}}\pi abc$	a, b, c = півосі еліпсоїда
Тор	$\left(\pi r^{2}\right)\left(2\pi R\right)=2\pi ^{2}Rr^{2}$	r = менший радіус (радіус труби), R = більший радіус (відстань від центра труби до центра тору)
Піраміда з прямокутною основою	${\frac {1}{3}}lwh$	l = довжина, w = ширина, h = висота
Конус	${\frac {1}{3}}\pi r^{2}h$	r = радіус кола основи, h = висота
Паралелепіпед	$abc{\sqrt {K}}$ ${\begin{aligned}K=1&+2\cos(\alpha )\cos(\beta )\cos(\gamma )\\&-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\end{aligned}}$	a, b, і c довжини ребер паралелепіпеда, а α, β, і γ це внутрішні кути між ребрами
Довільне тіло (з використанням інтегрального числення)	$\int A(h)\,dh$	Тут h — значення координати в довільному напрямку всередині фігури, A(h) = площа перпендикулярного до вибраного напряму перетину при значенні координати h

Величини об'єму, звісно, залежать від використаних величин довжини — якщо довжини виміряні в метрах, об'єм вимірюватиметься кубічними метрами тощо.

Співвідношення об'ємів конуса, кулі й циліндра однакового радіусу і висоти

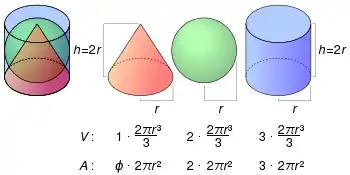
Конус, кулі і циліндр радіусу r і з висотою h

Вищенаведені формули можна використати для того, щоб показати що об'єми конуса, кулі і циліндра з однаковими радіусами і висотами мають пропорцію 1 : 2 : 3, відповідно.

Нехай радіус дорівнює r, а висота — h (що є 2r для кулі), тоді об'єм конуса становить

{\frac {1}{3}}\pi r^{2}h={\frac {1}{3}}\pi r^{2}\left(2r\right)=\left({\frac {2}{3}}\pi r^{3}\right)\times 1,

об'єм кулі становить

{\frac {4}{3}}\pi r^{3}=\left({\frac {2}{3}}\pi r^{3}\right)\times 2,

де об'єм циліндра —це

\pi r^{2}h=\pi r^{2}(2r)=\left({\frac {2}{3}}\pi r^{3}\right)\times 3.

Вперше співвідношення об'ємів кулі і циліндра становить 2 : 3 вважають було здійснено Архімедом.[1]

Куля

Об'єм кулі це інтеграл нескінченного числа нескінченно малих круглих дисків або кругів з товщиною dx. Розрахуємо об'єм кулі із центром 0 і радіусом r наступним чином.

Площа поверхні круга становить $\pi r^{2}$ .

Радіус кругів, визначено таким чином, що x-вісь проходить через них перпендикулярно, і

y={\sqrt {r^{2}-x^{2}}}

або

z={\sqrt {r^{2}-x^{2}}}

де y або z можуть бути прийняті для задавання радіусу кругу при конкретному значенні x.

Приймемо y за радіус диску, тоді об'єм кулі можна розрахувати наступним чином

\int _{-r}^{r}\pi y^{2}\,dx=\int _{-r}^{r}\pi \left(r^{2}-x^{2}\right)\,dx.

Тепер

\int _{-r}^{r}\pi r^{2}\,dx-\int _{-r}^{r}\pi x^{2}\,dx=\pi \left(r^{3}+r^{3}\right)-{\frac {\pi }{3}}\left(r^{3}+r^{3}\right)=2\pi r^{3}-{\frac {2\pi r^{3}}{3}}.

При поєднанні отримаємо $V={\frac {4}{3}}\pi r^{3}.$

Цю формулу можна вивести ще швидше використовуючи формулу для площі поверхні сфери, що дорівнює $4\pi r^{2}$ . Об'єм кулі заповнюється нескінченно тонкими поверхнями сфер різних радіусів, і тоді об'єм кулі становитиме.

\int _{0}^{r}4\pi r^{2}\,dr={\frac {4}{3}}\pi r^{3}.

Конус

Конус є фігурою пірамідальної форми.

Об'єм конуса це інтеграл нескінченної кількості тонких кругів з товщиною dx. Розрахунок об'єму конусу з висотою h, основа якого знаходиться в центрі координат (0, 0, 0) і має радіус r, є наступним.

Радіус плаского круга дорівнює r якщо x = 0 і 0 якщо x = h, і змінюється лінійно між цими значеннями,

r{\frac {h-x}{h}}.

Площа поверхні круга тоді становить

\pi \left(r{\frac {h-x}{h}}\right)^{2}=\pi r^{2}{\frac {(h-x)^{2}}{h^{2}}}.

Об'єм конуса тоді можна розрахувати так

\int _{0}^{h}\pi r^{2}{\frac {(h-x)^{2}}{h^{2}}}dx,

а після винесення констант

{\frac {\pi r^{2}}{h^{2}}}\int _{0}^{h}(h-x)^{2}dx

Після інтегрування отримаємо

{\frac {\pi r^{2}}{h^{2}}}\left({\frac {h^{3}}{3}}\right)={\frac {1}{3}}\pi r^{2}h.

Див. також

Засоби для вимірювання об'єму:

Бюретка
Піпетка
Мензурка
Елемент об'єму

Примітки

Rorres, Chris. Tomb of Archimedes: Sources. Courant Institute of Mathematical Sciences. Процитовано 2 січня 2007.

Посилання

Об'єм // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 136. — ISBN 978-966-7407-83-4.
Стаття УРЕ

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Rorres, Chris. Tomb of Archimedes: Sources. Courant Institute of Mathematical Sciences. Процитовано 2 січня 2007.