Спектр атома водню

До складу атома водню входить ядро з масою M і зарядом +e та електрон із зарядом -e. Взаємодія між ними — кулонівське притягання.

Гамільтоніан атома водню має вигляд [Прим. 1]

${\displaystyle {\hat {H}}=-{\frac {\hbar ^{2}}{2M}}\nabla _{R}^{2}-{\frac {\hbar ^{2}}{2m}}\nabla _{r}^{2}-{\frac {e^{2}}{|\mathbf {R} -\mathbf {r} |}}}$,

де ${\displaystyle \mathbf {R} }$ — радіус-вектор ядра, а ${\displaystyle \mathbf {r} }$ — радіус-вектор електрона.

При переході до системи координат, пов'язаної з центром мас, гамільтоніан розбивається на два незалежні доданки.

${\displaystyle {\hat {H}}=-{\frac {\hbar ^{2}}{2M_{C}}}\nabla _{R_{C}}^{2}+{\frac {\hbar ^{2}}{2\mu }}\nabla _{\rho }^{2}-{\frac {e^{2}}{\rho }}}$,

де ${\displaystyle M_{c}=M+m}$ — сумарна маса електрона й ядра, ${\displaystyle \mu ={\frac {Mm}{M+m}}}$ — приведена маса електрона, ${\displaystyle \mathbf {R} _{C}}$ — радіус-вектор центра мас, ${\displaystyle \mathbf {\rho } =\mathbf {r} -\mathbf {R} }$ — вектор, який сполучає ядро з електроном.

Перший член у гамільтоніані описує поступальний рух атома водню, як цілого. Надалі його не розглядатимемо.

У сферичній системі координат гамільтоніан відносного руху електрона навколо ядра записується у вигляді:

${\displaystyle {\hat {H}}=-{\frac {\hbar ^{2}}{2\mu }}{\frac {1}{\rho ^{2}}}{\frac {\partial }{\partial \rho }}\left(\rho ^{2}{\frac {\partial }{\partial \rho }}\right)-{\frac {{\hat {L}}^{2}}{2\mu \rho ^{2}}}-{\frac {e^{2}}{\rho }}}$ ,

де ${\displaystyle {\hat {L}}^{2}}$ — оператор квадрата кутового моменту.

Гамільтоніан комутує з оператором квадрата кутового моменту, а тому має спільні з ним власні функції.

Тривимірна візуалізація атомних орбіталей

Власні функції гамільтоніана мають вигляд:

${\displaystyle \psi _{nlm}={\tilde {\rho }}^{l}e^{-{\tilde {\rho }}/2}L_{n+l}^{2l+1}({\tilde {\rho }})Y_{lm}(\theta ,\varphi )}$,

де ${\displaystyle {\tilde {\rho }}={\frac {2\rho }{na_{0}}}}$, ${\displaystyle a_{0}}$ — радіус Бора, ${\displaystyle L_{i}^{j}}$ — поліноми Лаґерра, ${\displaystyle Y_{lm}(\theta ,\varphi )}$ — сферичні гармоніки.

Функції характеризуються трьома цілими квантовими числами

• n = 1,2,3… — основне квантове число.
• l = 0..n-1 — орбітальне квантове число.
• m = -l..l — магнітне квантове число.

Крім того, електронні хвильові функції характеризуються ще одним квантовим числом — спіном, який з'являється при врахуванні релятивістських ефектів. Спінове квантове число набуває значення ${\displaystyle s_{z}=\pm 1/2}$.

Власні значення гамільтоніана дорівнюють

${\displaystyle E_{n}=-R{\frac {1}{n^{2}}}}$,

де ${\displaystyle R={\frac {\mu \alpha ^{2}}{2\hbar ^{2}}}=\approx 13.6}$ еВ — константа (α — стала тонкої структури).

Власні значення гамільтоніана відповідають можливим значення енергії атома водню. Вони залежать тільки від основного квантового числа n. Кожен з енергетичних рівнів атома водню, крім першого, вироджений. Одному значенню енергії відповідає n² можливих функцій, а з урахуванням спіну — 2n². [Прим. 2]

В основному стані хвильова функція атома водню має вигляд:

${\displaystyle \psi _{1s}={\frac {1}{\sqrt {\pi }}}\left({\frac {Z}{a_{0}}}\right)^{3/2}e^{-Z\rho /a_{0}}}$,

де Z = 1 — зарядове число для ядра атома водню.

Окрім дискретних рівнів з від'ємною енергією атом водню має нескінченне число станів з додатньою енергією, в яких хвильові функції нелокалізовані. Ці стани відповідають іонізованому атому.

Спектральні лінії атома водню

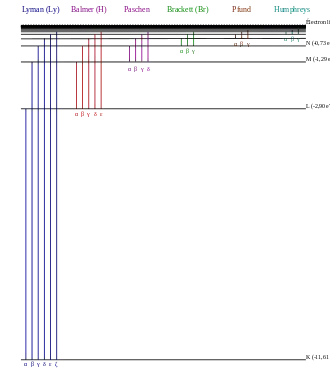
Згідно з положеннями квантової механіки (див. Золоте правило Фермі) при випромінюванні чи поглинанні світла квантовомеханічною системою має виконуватися закон збереження енергії. Наприклад, при випромінюванні кванта світла, енергія атома водню змінюється на величину ${\displaystyle \hbar \omega }$, де ω — циклічна частота світла. Але енергія атома водню може мати лише конкретні значення, визначені вище. Таким чином, атом водню в найнижчому основному стані не може випромінювати світло, бо не може зменшити своєї енергії. Якщо атом водню перебуває в першому збудженому стані, то при випромінюванні він може перейти лише в основний стан. При цьому енергія випроміненого фотона дорівнює різниці ${\displaystyle E_{1}-E_{0}}$. І так далі, атом у другому збудженому стані може перейти лише в основний стан і перший збуджений тощо.

При поглинанні світла атомом водню відбуваються схожі процеси. Атом в основному стані має енергію ${\displaystyle E_{0}}$ і може перейти в стани з енергією ${\displaystyle E_{n}}$. При цьому поглинаються виключно лише ті фонони, які мають енергії ${\displaystyle \hbar \omega =E_{n}-E_{0}}$.

Таким чином спектр поглинання й спектр випромінювання атома водню складається із серії тонких ліній, які згущуються до певної частоти (межі серії), а на вищих частотах перетворюється на неперервний спектр, оскільки високоенергетичні збудження відповідають іонізації атома, коли електрон, який відривається від ядра, може мати довільну енергію.

Лінійчастий спектр атома водню складається з ліній поглинання з частотами, які визначаються за формулою Рідберґа:

${\displaystyle \hbar \omega =R\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right)}$,

де m і n>m — цілі числа, m — головне квантове число. У спектрі виділяють:

• серію Лаймана (m = 1). Ця серія розташована в ультрафіолетовій області спектру й була підтверджена експериментально вже після того, як Нільс Бор передбачив її існування.
• серію Бальмера (m = 2). Перші лінії цієї серії лежать в оптичному діапазоні, а її межа (λ=364,6 нм) розташована в ближньому ультрафіолеті.
• серія Пашена (m = 3). Серія Пашена (як і всі наступні серії) лежить на інфрачервоній ділянці спектру.
• серія Брекета (m = 4).
• серія Пфунда (m = 5).

Тонка структура рівнів з n =2. Ліворуч — нерозщеплений рівень, який виникає в нерелятивістській теорії

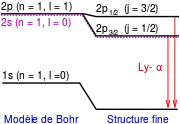
Приведений розрахунок енергетичного спектру атома водню ґрунтувався на рівнянні Шредінгера, яке не є Лоренц-інваріантним, а, отже, узгоджується з теорією відносності лише наближено. Релятивістським аналогом рівняння Шредінгера є рівняння Дірака. Суттєва відмінність рівняння Дірака від рівняння Шредінгера в тому, що рівняння Дірака вводить поняття спіна. Таким чином, крім наведених вище квантових чисел n, l, m, електрон атома водню характеризується ще й спіном. Кількісні поправки, які вносить у енергетичний спектр атома водню релятивістський розгляд, невеликі, бо середня швидкість електрона в атомі водню мала порівняно зі швидкістю світла. Однак, у спектрах є суттєва якісна відмінність. Ретельне вивчення спектрів показало, що лінії спектру розщеплюються на невеличкі серії. Це розщеплення отримало назву тонкої структури.

Як відомо, при врахуванні спіна, власні стани квантовомеханічних систем краще характеризувати не орбітальним квантовим числом l, а квантовим числом повного моменту j. Енергія власних станів атома водню приблизно дорівнює

${\displaystyle E_{n,j}=-{\frac {R}{n^{2}}}\left(1+{\frac {\alpha ^{2}}{n(j+1/2)}}-{\frac {3\alpha ^{2}}{4n^{2}}}+\dots \right)}$,

де ${\displaystyle \alpha =e^{2}/\hbar c}$ — універсальна стала, яка отримала назву сталої тонкої структури. Стала тонкої структури — мала величина (${\displaystyle \alpha \approx 1/137}$), а отже релятивістські поправки, які пропорційні квадрату сталої тонкої структури, є дуже малими. Однак, енергетичні рівні з певним n розщеплюються на кілька рівнів із різними j. Кожен такий рівень усе ще 2(2j+1) разів вироджений.

Наприклад, основний стан має l = 0, j = s = 1/2. Цей стан позначається 1S_1/2 [Прим. 3]. Він двократно вироджений і два можливі стани відповідають різним проекціям спіна ${\displaystyle s_{z}=\pm 1/2}$.

Перший збуджений стан розщеплюється на два:

• Стан 2P_3/2, для якого j = 3/2, l = 1. Цей стан чотирикратно вироджений.
• Стани 2S_1/2 (j= 1/2, l = 0) і 2P_1/2 (j = 1/2, l=1), кожен із яких теж двократно вироджений.

Надтонка структура виникає, якщо врахувати взаємодію спіна електрона зі спіном ядра (протона).

Основний енергетичний стан нейтрального атома водню розщеплюється на два близькі підрівні: верхній (збуджений) рівень відповідає паралельним спінам ядра та електрона, а нижній (основний) — антипаралельним. Перехід між ними пов'язаний із випромінюванням (або поглинанням) кванта з енергією ~ 5,874 33 µeV[1], що відповідає частоті 1 420 405 751,7667 ± 0,0009 Hz[2] (довжині хвилі  у вакуумі — 21,106 114 542 см). Цей перехід є забороненим (в електродипольному наближенні), однак він дозволений у магнітодипольному наближенні, щоправда, із надзвичайно малим коефіцієнтом — 2,9×10⁻¹⁵ с⁻¹, тобто, середній час існування збудженого стану становить близько 11 мільйонів років[3].

Спонтанний перехід у лабораторних умовах має дуже низьку інтенсивність. Але в астрономічних масштабах, завдяки поширеності атомарного водню, лінія досить інтенсивна. Вона лежить у мікрохвильовому діапазоні, в якому земна атмосфера майже прозора, тому її можна спостерігати безпосередньо з поверхні Землі. Дослідження лінії в радіоастрономії дає надзвичайно важливу інформацію про розподіл нейтрального Гідрогену в міжзоряному середовищі та галактиках[4].

Вимушене випромінювання на лінії 21 см застосовується для побудови гідрогенового мазера (квантового генератора частоти), що має досить високу точність (~10⁻¹³)[5].

Наведений вище опис оптичних переходів у атомі водню не враховує квантової природи світла. При квантовомеханічному розгляді фотони описуються рівняннями, аналогічними рівнянню квантового гармонічного осцилятора. Важливим фізичним наслідком квантового розгляду світла є існування нульових коливань навіть у тому випадку, коли кількість фотонів дорівнює нулю. Взаємодія квантовомеханічних систем із нульовими коливаннями призводить до спонтанного випромінювання, до невеличкого зсуву положення енергетичних рівнів і є причиною того, що лінії спектру не є нескінченно тонкими.

Для атома водню це має такі наслідки:

• Атом не може існувати в збудженому стані нескінченно довго. Рано чи пізно відбувається спонтанний перехід до основного стану з випромінюванням фотона.
• Кожна спектральна лінія природно уширена.
• Рівні атома водню дещо змішуються з положення, передбаченого формулами вище. Цей зсув, який отримав назву Лембового, різний для різних станів. Так, наприклад, навіть із врахуванням тонкого розщеплення рівні 2S_1/2 і 2P_1/2 мають однакову енергію. Однак, врахування взаємодії з нульовими коливаннями електромагнітного поля призводить до дуже малого розщеплення. Величина розщеплення дорівнює 1057,77(1) МГц. Таким чином, атом водню, збуджений у стан із головним квантовим числом n = 2, поглинає радіочастотне випромінювання завдяки переходам між 2S_1/2 і 2P_1/2 рівнями.

У зовнішньому магнітному полі вироджені енергетичні рівні з різними магнітними квантовими числами m розщеплюються. Це розщеплення пропорційне прикладеному полю. Відповідним чином розщеплюються лінії у спектрах випромінювання та поглинання.

Атом водню — єдина квантовомеханічна система, в якій в слабких електричних полях спостерігається лінійний ефект Штарка, тобто спектральні терми розщеплюються на компоненти, й величина розщеплення пропорційна електричному полю. Цей факт зумовлений виродженням ліній із різним значенням орбітального квантового числа l. Зовнішнє електричне поле частково знімає таке виродження.

Воднеподібні серії рівнів виникають в інших задачах квантової механіки. Серед них:

• Ізотопи водню: дейтерій та тритій мають енергетичні спектри, які відрізняються від спектра водню лише значенням зведеної маси. Ретельне вивчення оптичних переходів дозволяє перевірити справедливість основних формул.
• Йон гелію He⁺ та йон літію Li²⁺. Ці йони теж мають один електрон, але більший заряд ядра. Вивчаючи оптичні спектри цих йонів можна перевірити залаженість положення енергетичних рівнів від величини заряду.
• Зв'язані з протоном мюони. Мюони загалом схожі на електрони, але мають набагато більшу масу. Зв'язавшись із протонами вони утворюють воднеподібні атоми.
• Воднеподібні домішкові рівні в напівпровідниках. Донори й акцептори в напівпровідниках мають заряд, який відрізняється на одииницю від заряду сусідніх атомів. Проте завдяки великому значенню діелектричної проникності, електрони чи дірки слабо притягаються до цих атомів. Радіуси електронних орбіт в напівпровідниках загалом простягаються на десятки періодів кристалічної ґратки.
• Екситони Ваньє-Мотта — зв'язані стани електрона й дірки в напівпровідниках. Мають воднеподібну серію енергетичних станів.

• Білий М. У., Охріменко Б. А. Атомна фізика. — К. : Знання, 2009. — 559 с.
• Юхновський І. Р. Основи квантової механіки. — К. : Либідь, 2002. — 392 с.
• Ландау Л. Д., Лифшиц Е. М. Квантовая механика. Нерелятивистская теория // Теоретическая физика. — М. : Физматлит, 2008. — Т. 3. — 800 с.

• Молекула водню
• Атом
• Водневоподібний атом

Ця стаття належить до добрих статей української Вікіпедії.