Другий закон термодинаміки

Дру́гий зако́н термодина́міки встановлює існування ентропії у класичній термодинаміці [1] як функції стану термодинамічної системи і вводить поняття абсолютної термодинамічної температури)[2][3][4]. Тобто «другий закон є законом про ентропію»[5] і її властивості[6]. В ізольованій системі ентропія залишається або незмінною, або зростає (в нерівноважних процесах)[5], досягаючи максимуму при встановленні термодинамічної рівноваги (закон зростання ентропії) [2][3][2][3][4]. Різні формулювання другого закону термодинаміки, що зустрічаються в літературі, є окремі наслідки закону зростання ентропії[2][3][4].

Другий закон термодинаміки дозволяє побудувати раціональну температурну шкалу, що не залежить від довільності вибору термометричної властивості термодинамічного тіла і способу її вимірювання [7]. Разом перший і другий закони складають основу феноменологічної термодинаміки, яку можна розглядати як розвинену систему наслідків цих двох законів. При цьому, з усіх допустимих першим законом термодинаміки процесів в термодинамічній системі (тобто процесів, що не суперечать закону збереження енергії), другий закон дозволяє виділити фактично можливі процеси (тобто ті, що не суперечать законам термодинаміки) [7], встановити напрямок протікання мимовільних процесів, знайти граничне (найбільше або найменше) значення енергії, яке може бути корисним чином використано (отримано або витрачено) в термодинамічному процесі з урахуванням обмежень, що накладаються законами термодинаміки, а також сформулювати критерії рівноваги в термодинамічних системах [8][3][9].

Історична довідка

Саді Карно у своєму дослідженні «Роздуми про рушійну силу вогню і про машини, здатні розвивати цю силу» [10](1824), присвяченому паровим машинам, першим сформулював ідею, що лежить в основі другого закону термодинаміки: при відсутності різниці температур теплота не може бути перетворена в роботу; для постійного виробництва роботи тепловій машині необхідно мати принаймні два теплових резервуара з різними температурами — нагрівач і холодильник.

Вільям Томсон, (лорд Кельвін), відштовхуючись від роботи Карно, запропонував абсолютну термодинамічну шкалу температур (1848) і сформулював другий закон термодинаміки таким чином [11](1851): неможливий процес, єдиним результатом якого є отримання системою теплоти від одного джерела (теплового резервуара) і виконання нею еквівалентної кількості роботи[12]. З принципу Томсона випливає теорема Карно, на підставі якої вдається побудувати абсолютну термодинамічну шкалу температур[13].

Назва другий закон термодинаміки і історично перше його формулювання (1850) належать Рудольфу Клаузіусу (1850): неможливий процес, єдиним результатом якого є отримання системою теплоти від одного тіла і передача її іншому тілу, яке має більш високу температуру, ніж більш відома: Теплота не може переходити сама собою від більш холодного тіла до більш теплого. [14]).

Джозая Віллард Гіббс в опублікованій в 1876—1878 рр. роботі «Про рівновагу гетерогенних речовин»"[15] формулював закон зростання ентропії у вигляді принципу максимуму ентропії (по відношенню до всіх можливих її варіацій при постійній внутрішній енергії) в стані термодинамічної рівноваги, і вивів фундаментальні рівняння, що дозволяють визначати напрямок мимовільних процесів і умови термодинамічної рівноваги для систем будь-якої складності. Відзначимо, що до згаданого вище принципу максимуму ентропії еквівалентний сформульований Гіббсом принцип мінімуму внутрішньої енергії (в стані термодинамічної рівноваги внутрішня енергія ізольованої системи мінімальна[16]).

Людвіг Больцман в 1877 р. в роботі (рос) «О связи между вторым началом механической теории теплоты и теорией вероятностей в теоремах о тепловом равновесии»[17] показав зв'язок між ентропією і статистичною вагою (термодинамічною вірогідністю) макростану фізичної системи.[18]. Закон зростання ентропії у Больцмана отримав просту статистичну інтерпретацію: система прагне до найбільш вірогідного стану; мимоволі протікають тільки ті процеси, в яких система з менш вірогідного стану переходить у вірогідніше. Запропонована Больцманом інтерпретація ентропії як міри впорядкованості/невпорядкованості на атомно-молекулярному рівні дозволила виявити ряд важливих закономірностей, які стають очевидними, якщо замінити термін «ентропія» словом «невпорядкованість».

Вільгельм Оствальд в 1892 р. сформулював другий закон термодинаміки у вигляді твердження про неможливість створення вічного двигуна 2-го роду [19], тобто циклічно діючої ізотермічної теплової машини, здатної працювати від одного теплового резервуара і, отже, перетворювати в роботу всю енергію, видобуту з довкілля, що має постійну температуру. Неможливість створення вічного двигуна 2-го роду витікає безпосередньо з наведеного вище принципу Томсона і еквівалентна йому [20].

Герман фон Гельмгольц(1884) був першим, хто звернув увагу на ту обставину, що для визначення ентропії і абсолютної термодинамічної температури немає необхідності розглядати кругові процеси і залучати гіпотезу про існування ідеального газу, бо в дійсності абсолютна температура будь-якого тіла є не що інше, як той інтегруючий дільник для елементарного кількості теплоти, який залежить від однієї тільки температури тіла, відрахуваної за довільно обраною шкалою.[21][22].М. М. Шиллер, учень Гельмгольца, в своїх роботах 1887—1910 рр. [23] розвинув цю тезу[24], а Костянтин Каратеодорі (1909) обґрунтував ідею Гельмгольца за допомогою принципу адіабатної недосяжності[25]. У формулюванні другого закону термодинаміки Каратеодорі постулював існування поблизу кожного рівноважного стану системи таких її станів, які не можуть бути досягнуті з початкового стану за допомогою рівноважного адіабатного процесу. Недостатня наочність цього положення в роботі Каратеодорі компенсована ретельністю його математичного опрацювання.

У 1925 р. Тетяна Афанасьєва-Еренфест показала [26][27][28][29], що другий закон термодинаміки включає дві незалежні частини: твердження про існування ентропії і абсолютної термодинамічної температури, і закон зростання ентропії. У трактуванні Т. Афанасьєвої-Еренфест перша частина другого закону ґрунтована на чотирьох аксіомах і відноситься до станів рівноваги і рівноважних процесів, а друга — на двох аксіомах і відноситься до нерівноважних процесів.

У 1954 р. М. І. Білоконь на основі критичного аналізу різних формулювань другого закону прийшов до висновку, що «побудови принципу існування ентропії в рамках другого закону класичної термодинаміки на основі постулатів незворотності є помилкові і містять ряд неявних і абсолютно нестрогих допущень». Розвиваючи ідеї Т. Афанасьєвой-Еренфест Білоконь розділив другий закон термодинаміки на два закони: другий закон термостатики (принцип існування абсолютної термодинамічної температури і ентропії) і, власне, другий закон термодинаміки (принцип зростання ентропії в нерівноважних системах), а також запропонував незалежне від постулату незворотності обґрунтування принципу існування ентропії на основі очевидного симетричного постулату Білоконя [30].

Відкриття та становлення другого закону термодинаміки

«Історія відкриття другого закону термодинаміки є одною з найбільш чудових, повною драматизму глав загальної історії науки, останні сторінки якої ще далеко не дописані. Потрібні були зусилля не одного, а багатьох національних геніїв, для того щоб відкрити завісу над сокровенною таємницею природи, яку ми називаємо зараз другим законом термодинаміки». [31] Другий закон термодинаміки виник як робоча теорія теплових двигунів, що встановлює умови, при яких перетворення тепла на роботу досягає максимального ефекту. Теоретичні дослідження роботи теплових двигунів, уперше проведені французьким інженером Саді Карно, показали, що мала величина цього ефекту ─ коефіцієнта корисної дії (ККД) ─ обумовлюється не технічною недосконалістю теплових двигунів, а особливістю теплоти як способу передання енергії, яка накладає обмеження на його величину. Карно дійшов висновку, що ККД теплових машин не залежить від термодинамічного циклу і природи робочого тіла, а цілком визначається залежно від температур зовнішніх джерел ─ нагрівача і холодильника.(Теорема Карно). [32].

Робота Карно була написана до відкриття принципу еквівалентності теплоти і роботи і загального визнання закону збереження енергії. Свої висновки він засновував на двох суперечливих підставах: теорії теплецю, яка була незабаром відкинута, і гідравлічній аналогії. Дещо пізніше Р. Клаузиус і В. Томсон (Кельвін) погодили теорему Карно з законом збереження енергії і заклали основу того, що зараз становить зміст другого закону класичної (рівноважної) термодинаміки. [32].

Другий закон термодинаміки, також як і перший, являє собою узагальнення загальнолюдського досвіду. (Далі будуть розглянуті звичайні, тобто найбільш поширені термодинамічні системи, на відміну від тих, що рідко зустрічаються — незвичайних спінових систем, про які буде згадано окремо). Досвід показує, що теплота і робота, які є, за визначенням, формами передачі енергії, нерівноцінні. Якщо робота $A$ може безпосередньо переходити в теплоту, наприклад, за допомогою тертя, і при цьому змінюється стан одного тіла, то кількість теплоти $Q$ такою властивістю не володіє. Підведення тепла призводить лише до збільшення внутрішньої енергії системи, тобто до збільшення її параметрів, таких як температура, тиск, об'єм і т. д. Термодинамічна робота, вироблена за рахунок переданої кількості теплоти, може бути отримана лише опосередковано, шляхом зміни вищевказаних параметрів (наприклад, робота розширення робочого тіла). При цьому, крім охолодження самого джерела тепла, в разі незамкнутого процесу, відбувається зміна термодинамічної стану одного (робочого) тіла, а в разі замкнутого процесу ─ декількох тіл, яким робоче тіло повинне передати частину отриманого тепла. В тепловому двигуні одержувачем теплоти є холодильник. Процес віддачі частини тепла іншим тілам називається компенсацією. Як показує досвід, неможливо перетворити теплоту в роботу без компенсації, що є ціною, яку треба заплатити за це перетворення. Пояснемо на прикладі. Робота в теплових двигунах здійснюється шляхом розширення робочого тіла. Щоб зробити роботу машини безперервною, робоче тіло необхідно повернути в початковий стан. З цією метою його треба стиснути, витративши роботу. Якщо стиск робити при тій же температурі, що і розширення, то необхідно затратити всю роботу, отриману при розширенні, і ефективність цього двигуна буде дорівнювати нулю. Щоб робота стиснення, була менш за роботу розширення, необхідно проводити стиснення при нижчій температурі. Для зниження температури робочого тіла слід передати частину теплоти третьому тілу — холодильнику.

Коефіцієнт корисної дії теплового двигуна, за визначенням, дорівнює відношенню кількості теплоти, перетвореної на позитивну роботу за один цикл, до всієї підведеної до робочого тіла кількості теплоти.

\eta ={\frac {Q_{1}-Q_{2}}{Q_{1}}}=1-{\frac {Q_{2}}{Q_{1}}}={\frac {A}{Q_{1}}},

де $Q_{1}$ ─ кількість теплоти, отримана від нагрівача, $Q_{2}$ ─ кількість теплоти, віддана холодильнику, $A$ ─ термодинамічна робота.

Первісна аксіоматика другого закону термодинаміки

Для обґрунтування теореми Карно в згоді з законом збереження енергії і для подальшої побудови другого закону термодинаміки необхідно було ввести новий постулат. Нижче наведені найбільш поширені формулювання постулату другого закону термодинаміки, запропоновані в середині 19 го і на початку 20 го століть. (Слід зазначити, що в ряді робіт формулювання різних постулатів другого закону ототожнюються з формулюваннями власне другого закону термодинаміки. Це може створити хибне враження про неоднозначність самого другого закону термодинаміки. У інших роботах різні словесні формулювання відносяться до постулатів, а другим законом термодинаміки вважається його однозначний математичний вираз).

• Постулат Клаузіуса (1850 р.):

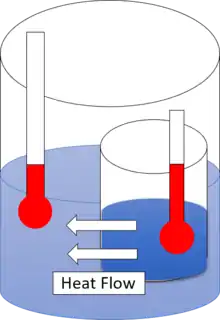
Теплота не може переходити мимовільно від більш холодного тіла до більш теплого.

• Постулат Томсона (Кельвіна) (1852 р .) в формулюванні М. Планка:

Неможливо побудувати періодично діючу машину, вся діяльність якої зводиться до підняття тяжкості і до охолодження теплового резервуара.

Вказівка на періодичність дії машини є істотною, оскільки можливо здійснити некруговой процес, єдиним результатом якого було б отримання роботи за рахунок внутрішньої енергії, отриманої від теплового резервуара. Цей процес не суперечить постулату Томсона, тому що при некруговому процесі машина не є періодично діючею. [33].

По суті постулат Томсона говорить про неможливість створення вічного двигуна другого роду, єдиним результатом роботи якого було перетворення тепла в роботу без компенсації, тобто без вимушеної передачі іншим тілам теплоти, яка буде безповоротно втрачена для отримання роботи. Неважко довести, що постулати Клаузіуса і Томсона еквівалентні. [34].

Цикл і теорема Карно

Теплові машини, до яких в термодинаміці відносять теплові двигуни, холодильні машини і теплові насоси, для забезпечення безперервної роботи повинні робити по замкнутому колу (циклу), при якому робоче тіло теплової машини періодично повертається в початковий стан. Одним з ідеалізованих циклів теплової машини є цикл, запропонований Саді Карно для аналізу роботи теплових машин з метою підвищення ефективності їх роботи.

Рис.1 Цикл Карно в координатах P і V

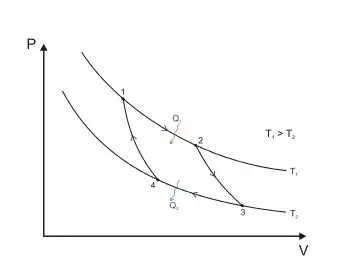
На рисунку 1 представлено оборотний цикл Карно, здійснений між двома джерелами теплоти постійної температури. Він складається з двох оборотних ізотермічних (1—2 і 3—4) і двох оборотних адіабатних (2—3 і 4—1) процесів. Робочим тілом цієї теплової машини є ідеальний газ. ( Основна стаття: Цикл Карно ). Теорема Карно стверджує, що термічний ККД оборотного циклу Карно не залежить від природи робочого тіла і визначається тільки температурами нагрівача $T_{1}$ і холодильника $T_{2}$ :

\eta ={\frac {T_{1}-T_{2}}{T_{1}}}=1-{\frac {T_{2}}{T_{1}}}

Інтеграл Клаузіуса і ентропія

Із зіставлення рівняння ККД оборотного циклу Карно

\eta ={\frac {T_{1}-T_{2}}{T_{1}}}=1-{\frac {T_{2}}{T_{1}}}

і рівняння ККД будь-якого циклу

\eta ={\frac {Q_{1}-Q_{2}}{Q_{1}}},

з урахуванням прийнятої системи знаків: плюс ─ для підведеного тепла і мінус ─ для відведеного, отримаємо

{\frac {Q_{1}}{T_{1}}}+{\frac {Q_{2}}{T_{2}}}=0

або

\sum {\frac {Q}{T}}=0

.

Цей вираз називається інтегралом або рівністю Клаузіуса. Іноді його називають першим інтегралом Клаузіуса. Так як при оборотному процесі інтеграл Клаузіуса, взятий по контуру циклу, дорівнює нулю, то його значення не залежить від шляху процесу, а визначається лише початковим і кінцевим станом тіла. Це означає, що підінтегральний вираз є повний диференціал деякої функції $(S)$ стану тіла (системи), яку Клаузіус назвав ентропією. Для нескінченно малого оборотного процесу

dS_{\text{обор}}={\frac {\delta Q_{\text{обор}}^{*}}{T}},

звідки

\delta Q_{\text{обр}}^{*}=TdS_{\text{обор}}

Оскільки елементарна кількість тепла $\delta Q$ не є повним диференціалом, а $dS$ є повний диференціал, то абсолютна температура $T$ виступає тут як інтегруючий дільник, який перетворює неповний диференціал $\delta Q$ в повний. Вираз $\delta Q_{\text{обор}}^{*}=TdS_{\text{обор}}$ являє собою математичний вираз другого закону термодинаміки для оборотних процесів або принцип існування ентропії. [35].

Розглянемо незворотний процес, представлений на рис. 2

Рис. 2 Незворотний процес

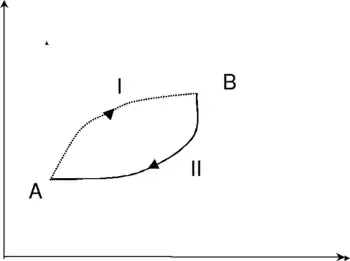
Він складається з двох частин: незворотного процесу AIB і оборотного BIIA, за допомогою якого тіло повертається в початковий стан. Цикл AIBIIA незворотний через незворотність процесу AIB. Перший інтеграл Клаузіуса можна записати у вигляді

\oint {\frac {\delta Q}{T}}=\int _{AIB}{\frac {\delta Q}{T}}-\int _{BIIA}{\frac {\delta Q}{T}}<0

Другий інтеграл, узятий по оборотному шляху AIIB, являє собою різницю $\Delta S$ ентропій між точками A і B. Звідси випливає, що для будь-якого незворотного процесу в будь-якій системі

\int _{A}^{B}{\frac {\delta Q}{T}}<\Delta S

Це вираження отримало назву другий інтеграл або нерівність Клаузіуса.

У диференціальному вигляді:

dS>{\frac {\delta Q}{T}}

Отже, в ізольованій системі, де $\delta Q^{*}=0$ ,

dS>0

Вираз $dS>0$ є принцип зростання ентропії ізольованих систем або математичний вираз другого закону термодинаміки для нерівноважних процесів. [36]

Загальний математичний вираз другого закону термодинаміки

Другий закон класичної термодинаміки формулюється як об'єднаний принцип існування і зростання ентропії ізольованих систем. З рівняння (1) і нерівності (2) :

dS={\frac {\delta Q^{*}}{T}}\geq 0.

Статистичне визначення ентропії

У статистичній фізиці ентропія $(S)$ термодинамічної системи розглядається як функція ймовірності $(W)$ її стану («принцип Больцмана»)

S=k\ln W,

де $k$ ─постійна Больцмана $W$ ─ термодинамічна вірогідність стану, яка визначається кількістю мікростанів, що реалізовують цей макростан.

Фізичний сенс ентропії

Серед величин, що визначають стан системи, ентропія займає особливе положення. Вона виділяється своєю абстрактністю, фізичний зміст ентропії не випливає безпосередньо з її математичного виразу і не піддається простому інтуїтивному уявленню. У зв'язку з цим неодноразово робилися спроби з'ясувати фізичний сенс ентропії. Одна із спроб була ґрунтована на пошуку аналогій ентропії з доступнішими для сприйняття поняттями. Наприклад, якщо елементарна робота є добуток сили на елементарне переміщення, то аналогом роботи може служити кількість теплоти, аналогом сили — абсолютна температура, а аналогом переміщення — ентропія. Очевидно, що аналогії подібного типу носять штучний характер, і користь від них для інтерпретації ентропії дуже сумнівна. Також неспроможною є спроба проведення аналогії ентропії з теплоємністю. Порівняємо вираження для питомої ентропії тіла :

$ds={\frac {\delta q}{T}}$

з вираженням питомої теплоємності :

$c={\frac {\delta q}{dT}}$ .

Подібність цих виразів полягає у використанні однакових величин і в однаковій розмірності теплоємності і ентропії. Обидві величини є кількістю теплоти, віднесеною до одиниці маси тіла і одиниці температури. Проте, якщо у формулі теплоємності температура входить в диференціальній формі і її можна вимірювати у будь-якій температурній шкалі, то у формулі ентропії фігурує абсолютна температура $T$ . Відмінність теплоємності від ентропії полягає в тому, що теплоємність є кількість теплоти, необхідна для нагрівання тіла масою 1 кг на один градус Цельсія (чи Кельвіна). При цьому значення теплоємності не залежить від вибору температурної шкали. Питома теплоємність $c$ має певне значення і є змінною величиною, якщо зазначений спосіб передачі теплоти, (наприклад, при постійному тиску, постійному об'ємі і так далі). Ентропія є кількість теплоти, віднесена до одиниці маси і одиниці абсолютної температури $T$ . В деякому розумінні це питома енергія. Ентропія є також функцією стану, але її значення не залежить від зміни системи поблизу заданого стану і вона є величиною статичною. З фізичної точки зору ентропія характеризує міру незворотності, неідеальності реального термодинамічного процесу. Вона є мірою дисипації (розсіювання) енергії, а також мірою оцінки енергії в плані її придатності (чи ефективності) використання для перетворення теплоти на роботу. [37] (Два останні твердження не відносяться до незвичайних систем з негативною абсолютною температурою, в яких теплота мимовільно може повністю перетворюватися на роботу).

Ревізія постулатної бази і проблема обґрунтування другого закону термодинаміки

На рубежі IX ─ XX століть стало очевидним, що постулати заборони Клаузіуса, Томсона й ін. абсолютно не відповідають змісту і сучасним вимогам, що пред'являються до обґрунтування принципу існування ентропії. Вони також не цілком задовольняють задачі обґрунтування принципу зростання ентропії, оскільки повинні містити вказівку про певну спрямованість незворотних явищ, що спостерігаються в природі, а не заперечення можливості їх протилежної течії. [38]. Щодо побудови другого закону термодинаміки за методом Клаузіуса було висловлено чимало заперечень і зауважень. Ось деякі з них:

Побудову принципу існування ентропії Клаузіус починає з виразу ККД оборотного циклу Карно для ідеальних газів, а потім поширює його на всі оборотні цикли. Таким чином Клаузіус неявно постулює можливість існування ідеальних газів, що підкоряються рівнянням Клапейрона $PV=RT$ і закону Джоуля $U=U(t)$ .
Постулат Клаузіуса не є явним твердженням, що вказує на напрямок протікання мимовільних процесів, що спостерігаються в природі, зокрема, на перехід тепла від більш нагрітого тіла до більш холодного, так як вираз не може переходити не є еквівалентом вислову переходить.
Затвердження статистичної фізики про вірогідний характер принципу незворотності і відкриття в 1951 р. «незвичайних» квантових систем з негативними абсолютними температурами, в яких: по-перше, мимовільний теплообмін має протилежний напрямок, по- друге, теплота може повністю перетворюватися у роботу, а робота не може повністю (без компенсації) перейти в тепло, похитнули базові постулати Клаузіуса, Томсона (Кельвіна) і Планка, повністю відкинувши одні, або наклавши серйозні обмеження на інші.

В XX столітті завдяки працям М. Шиллера, К. Каратеодорі, Т. Афанасьєвої-Еренфест, О. Гухмана, М. І. Білоконя та ін. в обґрунтуванні другого закону термодинаміки з'явився новий аксіоматичний напрямок. З'ясувалося, що принцип існування ентропії може бути обґрунтований незалежно від напрямку мимовільних процесів, що спостерігаються в природі, а також, виявилось, що для визначення абсолютної температури та ентропії не потрібно, як зауважив Гельмгольц, ні розгляду кругових процесів, ні припущення про існування ідеальних газів.

Метод Шиллера–Каратеодорі

У 1909 р. великий німецький математик Костянтин Каратеодорі, а ще раніше М. Шиллер обґрунтували принцип існування ентропії не шляхом дослідження станів реальних термодинамічних систем, а на основі математичного розгляду виразів оборотного теплообміну як диференціальних поліномів (форм Пфаффа). В основу методу було покладено

• Постулат Каратеодорі:

Поблизу кожного рівноважного стану системи можливі такі її стани, які не можуть бути досягнуті за допомогою оборотного адіабатичного процесу.

Теорема Каратеодорі стверджує: якщо диференціальний поліном Пфаффа $\sum X_{i}dx_{i}$ володіє тією властивістю, що у довільній близькості деякої точки існують інші точки, недосяжні за допомогою послідовних переміщень по шляху $\sum X_{i}dx_{i}=0$ , то існують інтегруючі дільники цього полінома і рівняння $\sum X_{i}dx_{i}=0$ .

Критично до постулату Каратеодорі ставився М. Планк. З його точки зору «висловлювання, що міститься в ньому, не є загальнозастасованим до природних процесів… . Ще ніхто і ніколи не ставив дослідів з метою досягнення всіх суміжних станів якогось певного стану адіабатичним шляхом». Системі Каратеодорі Планк протиставляє свою систему, засновану на постулаті:

• Постулат Планка:

Утворення теплоти за допомогою тертя незворотно.

Цим твердженням, на його думку, вичерпується зміст другого закону термодинаміки.

Між тим, метод Каратеодорі, отримав високу оцінку в роботі Т. Афанасьєвої-Еренфест (рос «Необратимость, односторонность и второе начало термодинамики» (1928 р.). У своїй чудовій статті Афанасьєва-Еренфест прийшла до ряду важливих висновків, зокрема:

1. Основний зміст другого закону полягає в тому, що елементарна кількість теплоти $\delta Q$ , якою система обмінюється в квазістатичному процесі, може бути представлена у вигляді $TdS$ , де $T=f(t)$ ─ універсальна функція температури, що називається абсолютною температурою, а $(S)$ ─ функція параметрів стану системи, що дістала назву ентропії. Саме ж вираження $\delta Q=TdS$ являє собою принцип існування ентропії.

2. Принципова відмінність нерівноважних процесів від рівноважних полягає в тому, що в умовах неоднорідності температурного поля усередині термодинамічної системи, а також завдяки втратам роботи у незворотних процесах на тертя і внутрішній опір, можливий перехід системи до стану з іншою ентропією без обміну теплотою з довкіллям. (Цей процес пізніше в працях М. І. Білоконя дістав назву внутрішнього теплообміну або теплообміну робочого тіла). Внутрішній теплообмін в ізольованій системі завжди є незворотним і слідством його є однобічність.

3. Одностороння зміна ентропії в рівній мірі мислима і як неухильне її зростання, і як неухильне убування. Фізичні передумови, такі як адіабатична недосяжність і безповоротність реальних процесів, не виражають ніяких вимог відносно переважного напряму течії мимовільних процесів.

4. Для узгодження отриманих виведень з даними досвіду для реальних процесів необхідно прийняти постулат, сфера дії якого визначається межами застосовності цих даних. Таким постулатом є принцип зростання ентропії ізольованих систем.

О. Гухман, оцінюючи роботу Каратеодорі, вважає, що вона «відрізняється формальною логічною строгістю і бездоганністю в математичному відношенні… Разом з тим, у прагненні до найбільшої загальності Каратеодорі надав своїй системі настільки абстрактну і складну форму, що вона виявилася фактично недоступною для більшості фізиків того часу». Відносно постулату адіабатичної недосяжності Гухман зауважує, що як фізичний принцип він не може бути покладений в основу теорії, що має універсальне значення, оскільки не володіє властивістю самоочевидності. «Все гранично ясно відносно простої системи……Але ця ясність повністю втрачається в загальному випадку гетерогенної системи, ускладненою хімічними перетвореннями і відчуває вплив зовнішніх полів» [39]. Щодо побудови основ термодинаміки Гухман вважає, що «самостійної окремої проблеми існування ентропії немає. Питання зводиться до поширення, на випадок термічної взаємодії, досвіду вивчення всіх інших енергетичних взаємодій, що завершуються встановленням однакового по формі рівняння для елементарного кількості впливу $dQ=Pdx$ . Ця екстраполяція дає підстави прийняти її в якості правдоподібної гіпотези і тим самим постулювати існування ентропії. (Тут слід зауважити, що постулювання принципу існування ентропії на основі загальнолюдського досвіду істотно обмежує сферу його дії як фундаментального закону природи).

М. І. Білоконь у своїй монографії „Термодинаміка“ дав детальний аналіз численних спроб обґрунтування другого закону термодинаміки як об'єднаного принципу існування і зростання ентропії на основі одного лише постулату незворотності. Він показав, що спроби такого обґрунтування не можуть бути виправдані, по-перше, тому, що висновок про існування ентропії і абсолютної температури не має ніякого відношення до незворотності явищ природи, оскільки ці функції існують незалежно від зростання або зменшення ентропії ізольованих систем, по-друге, вказівка про направлення спостережуваних незворотних явищ знижує рівень загальності другого закону термодинаміки і, по-третє, використання постулату Томсона — Планка про неможливість повного перетворення тепла в роботу суперечить результатам досліджень систем з негативною абсолютною температурою, в яких може бути здійснено повне перетворення теплоти в роботу, але неможливо повне перетворення роботи в теплоту.

Слідом за Т. Афанасьєвої-Еренфест М. І. Білоконь стверджує, що відмінність змісту, рівня загальності і сфери застосування принципів існування і зростання ентропії абсолютно очевидно:

1. З принципу існування ентропії випливає ряд найважливіших диференціальних рівнянь термодинаміки. Його наукове і практичне значення важко переоцінити.

2. Принцип зростання ентропії ізольованих систем є твердження про незворотну течію спостережуваних природних явищ. Цей принцип використовується в судженнях про найбільш вірогідний напрямок течії фізичних і хімічних процесів. З нього випливають всі нерівності термодинаміки.

Відносно обґрунтування принципу існування ентропії за методом Шиллера ─ Каратеодорі Білоконь зазначає, що в побудовах за цим методом абсолютно обов'язковим є використання теореми Каратеодорі про умови існування інтегруючих дільників диференціальних поліномів $\delta Q=\sum X_{i}dx_{i}=\tau dZ$ проте, необхідність використання цієї теореми „повинна бути визнана дуже сором'язливою, так як загальна теорія диференціальних поліномів розглянутого типу (форм Пфаффа) представляє відомі труднощі і викладається лише в спеціальних працях з вищої математики.“ У більшості курсів термодинаміки теорема Каратеодорі дається без доведення, або наводиться доказ в нестрогому, спрощеному вигляді. [40]

Аналізуючи побудову принципу існування ентропії рівноважних систем за схемою К. Каратеодорі, М. І. Білоконь звертає увагу на використання необґрунтованого припущення про можливість одночасного включення температури $t$ і $Z$ ─ функції до складу незалежних змінних стану рівноважної системи і приходить до висновку, що постулат Каратеодорі, еквівалентний групі загальних умов існування інтегруючих дільників диференціальних поліномів $\sum X_{i}dx_{i},$ є недостатнім для встановлення існування первинного інтегруючого дільника $\tau (t)=T$ , тобто для обґрунтування принципу існування абсолютної температури і ентропії. Далі він стверджує, що при побудові принципу існування абсолютної температури і ентропії на основі теореми Каратеодорі повинен бути використаний такий постулат, який був би еквівалентним теоремі про несумісність адіабати і ізотерми. У цих коректованих побудовах стає абсолютно зайвим постулат Каратеодорі, тому що він є окремим слідством необхідної теореми про несумісність адіабати і ізотерми» [41].

Метод М. І. Білоконя

По методу Білоконя другий закон термодинаміки розділено на два незалежні принципи (закони) :

1. Принцип існування абсолютної температури і ентропії (другий закон термостатики).

2. Принцип зростання ентропії (другий закон термодинаміки).

Кожен з цих принципів отримав обґрунтування на підставі незалежних постулатів.

Постулат другого закону термостатики (Білоконя) :

Температура є єдина функція стану, що визначає напрям мимовільного теплообміну, тобто між тілами і елементами тіл, що не знаходяться в тепловій рівновазі, неможливий одночасний мимовільний (по балансу) перехід тепла в протилежних напрямках — від тіл більш нагрітих до тіл менш нагрітих і навпаки. [42]

Постулат Білоконя самоочевидний, оскільки є окремим вираженням причинного зв'язку і однозначності законів природи. Наприклад, якщо існує причина, в силу якої в системі тепло переходить від більш нагрітого тіла до менш нагрітого, то ця ж причина перешкоджатиме переходу тепла в протилежному напрямку і навпаки. Цей постулат є повністю симетричний відносно напряму незворотних явищ, оскільки не містить ніяких вказівок про напрям незворотних явищ, що спостерігаються у нашому світі ─ світі позитивних абсолютних температур.

Слідства другого закону термостатики: Слідство I. Неможливо одночасне (в рамках однієї і тієї ж просторово — часової системи позитивних або негативних абсолютних температур) здійснення повних перетворень тепла в роботу і роботи в тепло.

Слідство II. (Теорема несумісності адіабати і ізотерми). На ізотермі рівноважної термодинамічної системи, яка перетинає дві різні адіабати тієї ж системи, теплообмін не може дорівнювати нулю.

Слідство III. (Теорема теплової рівноваги тіл). В рівноважних кругових процесах двох термічно спряжених тіл $(t_{I}=t_{I}I)$ , що утворюють адіабатично ізольовану систему, обидва тіла повертаються на вихідні адіабати і в початковий стан одночасно.

На підставі слідств постулату другого закону термостатики М. І. Білоконь запропонував три схеми побудови принципу існування абсолютної температури і ентропії для оборотних і незворотних процесів $\delta Q=\delta Q^{*}+Q^{**}TdS.$ [43].

Постулат другого закону термодинаміки :

Робота може бути безпосередньо і повністю перетворена і тепло шляхом тертя або електронагріву.

Слідство I. Тепло не може бути повністю перетворене на роботу (принцип виключеного Perpetuum mobile II роду) :

\eta <1

.

Слідство II. ККД або холодопродуктивність будь-якої незворотної теплової машини при заданих температурах зовнішніх джерел завжди менше ККД або холодопродуктивності оборотних машин, працюючих між тими ж джерелами.

Зниження ККД і холодопродуктивності реальних теплових машин пов'язане з нерівноважним теплообміном через різницю температур джерел теплоти і робочого тіла, а також за рахунок незворотних втрат роботи на тертя і внутрішні опори. З цього слідства і слідства I другого закону термостатики безпосередньо витікає неможливість здійснення Perpetuum mobile I і II роду.

У системі ідей Клаузіуса і його послідовників обидва принципи існування і зростання ентропії ґрунтуються на постулаті незворотності(постулати Клаузіуса, Томсона-Кельвіна, Планка та ін.), причому на перше місце поставлений принцип зростання ентропії, який зводиться в ранг універсального закону природи, що стоїть поряд із законом збереження енергії. Абсолютизація Клаузіусом принципу зростання ентропії набула сенсу найважливішого космологічного закону природи, наслідком якого стала антинаукова концепція теплової смерті Всесвіту. [44]. Таким чином, будь-яке порушення цього фундаментального закону привело б до обвалення усіх слідств з нього, що істотно обмежило б сферу впливу термодинаміки. Характерним в цьому сенсі є висловлювання М. Планка, який стверджував, що з незворотністю «стоїть і падає термодинаміка». У цьому сенсі висновки статистичної фізики про вірогідний характер принципу незворотності, а також відкриття систем з негативними абсолютними температурами повинні привести до краху другого закону, а разом з ним і самої термодинаміки. Проте цього не сталося. Помилковий висновок М.Планка про «падіння термодинаміки» з падінням постулату безповоротності безпосередньо пов'язаний з об'єднанням в одному законі принципів існування і зростання ентропії, що склалось історично, і наданням принципу зростання ентропії сенсу другого закону термодинаміки. На нерівноцінність вказаних принципів і несумісність їх в одному законі звернула увагу Т. Афанасьєва-Еренфест. За її словами, один і той же закон представляється в двох абсолютно різних видах: 1) як твердження існування інтегруючого множника для відомого виразу $\delta Q$ і 2) як твердження про неухильне зростання ентропії у реальних адіабатичних процесах. Представляється важким вмістити в одне чітке осяжне поле зору ці обидва положення і схопити логічну тотожність другого закону і принципу зростання ентропії. [45].

Завдяки ревізії другого закону термодинаміки на перший план в якості фундаментального закону термодинаміки виходить принцип існування ентропії, а принцип зростання ентропії ізольованих систем є принципом локальним, статистичним, який, за словами Афанасьевой-Эренфест, виконується «тільки в деякі епохи».[46]

Гіпотеза «теплової смерті Всесвіту»

Некритичне узагальнення закономірностей земного досвіду, зокрема, поширення висновків другого закону термодинаміки про зростання ентропії ізольованих систем на системи галактичного розміру, де значну роль у формуванні нових зоряних систем грають гравітаційні сили, і на Всесвіт в цілому призводило в минулому до антинаукового висновку про теплову смерть Всесвіту. Згідно з сучасними даними Метагалактика являє собою систему, що розширюється і є нестаціонарною, і тому питання про теплову смерть Всесвіту не можна навіть ставити. [47]

Примітки

Термін(дав.-гр. ἐντροπία) утворений Р. Клаузіусом із слова τροπη — перетворення, і приставки ἐν — в, всередину (Другий закон термодинаміки, 1934, с. 156). Самого слова ἐντροπία, того, що відповідає українським словосполученням «зміст зміни», «кількість перетворення», в старогрецькій мові немає.
БСЭ, 3-е изд., т. 5, 1971, с. 495.
Физика. Большой энциклопедический словарь, 1998, с. 95.
Химическая энциклопедия, т. 1, 1988, с. 432.
Базаров И. П., Термодинамика, 2010, с. 49.
Ця дефініція не накладає обмежень на вигляд термодинамічної системи, тому цілком коректно міркувати про ентропію нерівноважних систем, у тому числі відкритих і релятивістських.
Сивухин Д. В., Общий курс физики т. II, 2005, с. 85.
БСЭ, & nbsp;3-е изд., & nbsp; т. & nbsp;5, 1971, с. 495.
Химическая энциклопедия, т. 1/1988, с. 432.
Второе начало термодинамики, 1934, с. 16—69.
Второе начало термодинамики, 1934, с. 165.
«Якби ми не визнали цю аксіому дійсної при всіх температурах, нам довелося б допустити, що можна ввести в дію автоматичну машину і отримувати шляхом охолодження моря або землі механічну роботу в будь-якій кількості, аж до вичерпання всієї теплоти суші і моря або, врешті-решт, всього матеріального світу» (Второе начало термодинамики, 1934, с. 165).
БСЭ, т. 6, 2006, с. 80—81.
Второе начало термодинамики, 1934, с. 133.
Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 61—350.
Герасимов Я. И. и др., Курс физической химии, т. 1, 1970, с. 117.
Больцман Л., Избранные труды, 1984, с. 190—235.
Термодинамічна вірогідність — число способів, якими може бути реалізований стан фізичної системи. У термодинаміці макростан фізичної системи характеризується певними значеннями щільності, тиску, температури і інших вимірних макроскопічних величин. Одному і тому ж макростану часток, що хаотично переміщаються, можуть відповідати різні квантові мікростани з однаковою енергією Термодинамічна вірогідність W дорівнює числу мікростанів, що реалізовують цей макростан, з чого виходить, що W є безрозмірне ціле число, більше або рівне 1, і не є вірогідністю в математичному сенсі; менш впорядкованим станам відповідає більше значення W або, що те ж саме, ці стани мають більшу статистичну вагу. Найменше значення W = 1 має найбільш впорядкована система — ідеальний кристал при температурі абсолютного нуля. Термодинамічна вірогідність пов'язана з однією з основних макроскопічних характеристик системи — ентропією — рівнянням Больцмана. Для обчислення W істотно, чи вважають частки системи помітними або невиразними.
Бродянский В. М., Вечный двигатель, 1989, с. 114.
БРЭ, т. 6, 2006, с. 80—81.
Helmholtz H. v., Studien zur Statik monocyklischer Systeme, 1884.
Гухман А. А., Об основаниях термодинамики, 2010, с. 352.
Гельфер Я. М., История и методология термодинамики и статистической физики, 1981, с. 209—212.
«Формулювання другого закону вимагає, щоб при будь-якому адіабатному процесі, при будь-якому адіабатному процесі, при якому параметри стану повертаються до своїх первинних значень, температура також наводилася до своєї первинної величини. Ця вимога виконується перш за все тоді, коли приріст температури не буде залежати від проміжних значень параметрів стану, тобто перш за все, коли будь-яка з температур адиабатного процесу визначиться тільки в функції відповідних параметрів … А ця обставина, очевидно, відповідає тій умові, щоб рівняння dQ= 0 мало інтеграл» (Звіти та протоколи фізико-математичного товариства при університеті св. Володимира. Київ, 1899, с. 8. Цитується за книгою «Гельфер Я. М., История и методология термодинамики и статистической физики», 1981, с. 210).
Каратеодори К., Об основах термодинамики.
Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (1), 1925.
Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (2), 1925.
(рос.) Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928.
Ehrenfest-Afanassjewa T. Die Grundlagen der Thermodynamik, 1956.
Белоконь Н. И.,Термодинамика, 1954, с. 5—6.
Вукалович М. П., Техническая термодинамика, 1968, с. 94—95.
Белоконь Н. И.,Термодинамика, 1954, с. 131.
Сивухин Д. В., Общий курс физики т. II, 2005, с. 88.
Сивухин Д. В., Общий курс физики т. II, 2005, с. 90.
Базаров И. П., Термодинамика, 2010, с. 58.
Базаров И. П., Термодинамика, 2010, с. 75.
Шамбадаль П., Развитие и приложение энтропии, 1967, с. 61—64.
Белоконь Н. И.,Термодинамика, 1954, с. 197—198.
Гухман А. А., Об основаниях термодинамики, 2010, с. 370.
Белоконь Н. И.,Термодинамика, 1954, с. 244.
Белоконь Н. И.,Термодинамика, 1954, с. 245—246.
Белоконь Н. И., Основные принципы термодинамики, 1968, с. 55—56.
Белоконь Н. И.,Термодинамика, 1954, с. 166—184.
Гухман А. А., Об основаниях термодинамики, 2010, с. 351.
Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928, с. 3.
Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928, с. 26—27.
Базаров И. П., Термодинамика, 2010, с. 82─84..

Джерела

Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik // Zeitschrift für Physik. — 1925. — Bd. 33, Nr. 1. — S. 933–945.
Ehrenfest-Afanassjewa T.]] Berichtigung zu der Arbeit: Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik // Zeitschrift für Physik. — 1925. — Bd. 34, Nr. 1. — S. 638.
Ehrenfest-Afanassjewa T. Die Grundlagen der Thermodynamik. — E. J. Brill, 1956. — XII + 131 p.
Helmholtz Hermann von. Studien zur Statik monocyklischer Systeme // Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. — 1884. — Nr. 1. Halbband. — S. 159—177.
Афанасьева-Эренфест, Т. А. Необратимость, односторонность и второе начало термодинамики // Журнал прикладной физики. — 1928. — Т. 5, № 3—4. — С. 3—30.
Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар : Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература) — ISBN 978-5-8114-1003-3.
Белоконь, Н. И. Термодинамика. — М. : Госэнергоиздат, 1954. — 417 с.
Белоконь Н. И. Основные принципы термодинамики. — М. : Недра, 1968. — 112 с.
Больцман Л. Избранные труды / Отв. ред. Л. С. Полак. — М. : Наука, 1984. — 590 с. — (Классики науки)
Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская Энциклопедия, 1971. — Т. 5: Вешин — Газли. — 640 с.
Большая российская энциклопедия / Гл. ред. Ю. С. Осипов. — М. : Большая Российская энциклопедия, 2006. — Т. 6: Восьмеричный путь — Германцы. — 768 с. — ISBN 5-85270-335-4.
Бродянский В. М. Вечный двигатель — прежде и теперь. От утопии — к науке, от науки — к утопии. — М. : Энергоатомиздат, 1989. — 256 с. — (Научно-популярная библиотека школьника) — ISBN 5-283-00058-3.
Вукалович М. П. Техническая термодинамика. — М. : Энергия, 1968. — 496 с.
Второе начало термодинамики: Сади Карно — В. Томсон-Кельвин — Р. Клаузиус — Л. Больцман — М. Смолуховский / Под. ред. и с пред. А. К. Тимирязева. — М.—Л. : Гостехиздат, 1934. — 311 с.
Гельфер Я. М. История и методология термодинамики и статистической физики. — 2-е изд., перераб. и доп. — М. : Высшая школа. — 536 с.
Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М. : Химия, 1970. — Т. I. — 592 с.
Гиббс Дж. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М. : Наука, 1982. — 584 с. — (Классики науки).
Гухман, А. А. Об основаниях термодинамики. — 2-е изд. — ЛКИ, 2010. — 384 с. — ISBN 978-5-382-01105-9.
Каратеодори, К. Об основах термодинамики // Развитие современной физики / Отв. ред. Б. Г. Кузнецов. — М. : Наука, 1964. — С. 3—22.
Сивухин Д. В. Общий курс физики. — 5-е изд. — М. : Физматлит, 2005. — Т. II. — 544 с. — ISBN 5-9221-0601-5.
Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М. : Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
Химическая энциклопедия / Гл. ред. И. Л. Кнунянц. — М. : Большая Российская энциклопедия, 1988. — Т. 1: Абл — Дар. — 624 с.
Шамбадаль П.,. Развитие и приложение понятия энтропии. — М. : Наука, 1967. — 280 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Термін(дав.-гр. ἐντροπία) утворений Р. Клаузіусом із слова τροπη — перетворення, і приставки ἐν — в, всередину (Другий закон термодинаміки, 1934, с. 156). Самого слова ἐντροπία, того, що відповідає українським словосполученням «зміст зміни», «кількість перетворення», в старогрецькій мові немає.

[FOOTNOTEБСЭ,&nbsp;3-е_изд.,&nbsp;т.&nbsp;51971495-2] БСЭ, 3-е изд., т. 5, 1971, с. 495.

[FOOTNOTEФизика.&nbsp;Большой&nbsp;энциклопедический&nbsp;словарь199895-3] Физика. Большой энциклопедический словарь, 1998, с. 95.

[FOOTNOTEХимическая&nbsp;энциклопедия,&nbsp;т.&nbsp;11988432-4] Химическая энциклопедия, т. 1, 1988, с. 432.

[FOOTNOTEБазаров_И._П.,_Термодинамика201049-5] Базаров И. П., Термодинамика, 2010, с. 49.

[6] Ця дефініція не накладає обмежень на вигляд термодинамічної системи, тому цілком коректно міркувати про ентропію нерівноважних систем, у тому числі відкритих і релятивістських.

[FOOTNOTEСивухин&nbsp;Д.&nbsp;В.,_Общий&nbsp;курс&nbsp;физики&nbsp;т.&nbsp;II200585-7] Сивухин Д. В., Общий курс физики т. II, 2005, с. 85.

[FOOTNOTEБСЭ,_&_nbsp;3-е_изд.,_&_nbsp;_т._&_nbsp;51971495-8] БСЭ, & nbsp;3-е изд., & nbsp; т. & nbsp;5, 1971, с. 495.

[FOOTNOTEХимическая&nbsp;энциклопедия,&nbsp;т.&nbsp;1/1988432-9] Химическая энциклопедия, т. 1/1988, с. 432.

[FOOTNOTEВторое&nbsp;начало&nbsp;термодинамики193416—69-10] Второе начало термодинамики, 1934, с. 16—69.

[FOOTNOTEВторое&nbsp;начало&nbsp;термодинамики1934165-11] Второе начало термодинамики, 1934, с. 165.

[12] «Якби ми не визнали цю аксіому дійсної при всіх температурах, нам довелося б допустити, що можна ввести в дію автоматичну машину і отримувати шляхом охолодження моря або землі механічну роботу в будь-якій кількості, аж до вичерпання всієї теплоти суші і моря або, врешті-решт, всього матеріального світу» (Второе начало термодинамики, 1934, с. 165).

[FOOTNOTEБСЭ,&nbsp;т.&nbsp;6200680—81-13] БСЭ, т. 6, 2006, с. 80—81.

[FOOTNOTEВторое&nbsp;начало&nbsp;термодинамики1934133-14] Второе начало термодинамики, 1934, с. 133.

[FOOTNOTEГиббс&nbsp;Дж.&nbsp;В.,_Термодинамика.&nbsp;Статистическая&nbsp;механика198261—350-15] Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 61—350.

[FOOTNOTEГерасимов_Я._И._и_др.,_Курс_физической_химии,_т.&nbsp;11970117-16] Герасимов Я. И. и др., Курс физической химии, т. 1, 1970, с. 117.

[FOOTNOTEБольцман&nbsp;Л.,_Избранные&nbsp;труды1984190—235-17] Больцман Л., Избранные труды, 1984, с. 190—235.

[18] Термодинамічна вірогідність — число способів, якими може бути реалізований стан фізичної системи. У термодинаміці макростан фізичної системи характеризується певними значеннями щільності, тиску, температури і інших вимірних макроскопічних величин. Одному і тому ж макростану часток, що хаотично переміщаються, можуть відповідати різні квантові мікростани з однаковою енергією Термодинамічна вірогідність W дорівнює числу мікростанів, що реалізовують цей макростан, з чого виходить, що W є безрозмірне ціле число, більше або рівне 1, і не є вірогідністю в математичному сенсі; менш впорядкованим станам відповідає більше значення W або, що те ж саме, ці стани мають більшу статистичну вагу. Найменше значення W = 1 має найбільш впорядкована система — ідеальний кристал при температурі абсолютного нуля. Термодинамічна вірогідність пов'язана з однією з основних макроскопічних характеристик системи — ентропією — рівнянням Больцмана. Для обчислення W істотно, чи вважають частки системи помітними або невиразними.

[FOOTNOTEБродянский&nbsp;В.&nbsp;М.,&nbsp;Вечный&nbsp;двигатель1989114-19] Бродянский В. М., Вечный двигатель, 1989, с. 114.

[FOOTNOTEБРЭ,&nbsp;т.&nbsp;6200680—81-20] БРЭ, т. 6, 2006, с. 80—81.

[FOOTNOTEHelmholtz_H._v.,_Studien_zur_Statik_monocyklischer_Systeme1884-21] Helmholtz H. v., Studien zur Statik monocyklischer Systeme, 1884.

[FOOTNOTEГухман&nbsp;А.&nbsp;А.,_Об&nbsp;основаниях&nbsp;термодинамики2010352-22] Гухман А. А., Об основаниях термодинамики, 2010, с. 352.

[FOOTNOTEГельфер_Я._М.,_История_и_методология_термодинамики_и_статистической_физики1981209—212-23] Гельфер Я. М., История и методология термодинамики и статистической физики, 1981, с. 209—212.

[24] «Формулювання другого закону вимагає, щоб при будь-якому адіабатному процесі, при будь-якому адіабатному процесі, при якому параметри стану повертаються до своїх первинних значень, температура також наводилася до своєї первинної величини. Ця вимога виконується перш за все тоді, коли приріст температури не буде залежати від проміжних значень параметрів стану, тобто перш за все, коли будь-яка з температур адиабатного процесу визначиться тільки в функції відповідних параметрів … А ця обставина, очевидно, відповідає тій умові, щоб рівняння dQ= 0 мало інтеграл» (Звіти та протоколи фізико-математичного товариства при університеті св. Володимира. Київ, 1899, с. 8. Цитується за книгою «Гельфер Я. М., История и методология термодинамики и статистической физики», 1981, с. 210).

[FOOTNOTEКаратеодори&nbsp;К.,&nbsp;Об&nbsp;основах&nbsp;термодинамики-25] Каратеодори К., Об основах термодинамики.

[FOOTNOTEEhrenfest-Afanassjewa&nbsp;T.&nbsp;Zur&nbsp;Axiomatisierung&nbsp;des&nbsp;zweiten&nbsp;Hauptsatzes&nbsp;der&nbsp;Thermodynamik&nbsp;(1)1925-26] Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (1), 1925.

[FOOTNOTEEhrenfest-Afanassjewa&nbsp;T.&nbsp;Zur&nbsp;Axiomatisierung&nbsp;des&nbsp;zweiten&nbsp;Hauptsatzes&nbsp;der&nbsp;Thermodynamik&nbsp;(2)1925-27] Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (2), 1925.

[FOOTNOTE(рос.)_Афанасьева-Эренфест&nbsp;Т.&nbsp;А.,_Необратимость,&nbsp;односторонность&nbsp;и&nbsp;второе&nbsp;начало&nbsp;термодинамики1928-28] (рос.) Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928.

[FOOTNOTEEhrenfest-Afanassjewa_T._Die_Grundlagen_der_Thermodynamik1956-29] Ehrenfest-Afanassjewa T. Die Grundlagen der Thermodynamik, 1956.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,Термодинамика19545—6-30] Белоконь Н. И.,Термодинамика, 1954, с. 5—6.

[FOOTNOTEВукалович&nbsp;М.&nbsp;П.,&nbsp;Техническая&nbsp;термодинамика196894—95-31] Вукалович М. П., Техническая термодинамика, 1968, с. 94—95.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,Термодинамика1954131-32] Белоконь Н. И.,Термодинамика, 1954, с. 131.

[FOOTNOTEСивухин&nbsp;Д.&nbsp;В.,_Общий&nbsp;курс&nbsp;физики&nbsp;т.&nbsp;II200588-33] Сивухин Д. В., Общий курс физики т. II, 2005, с. 88.

[FOOTNOTEСивухин&nbsp;Д.&nbsp;В.,_Общий&nbsp;курс&nbsp;физики&nbsp;т.&nbsp;II200590-34] Сивухин Д. В., Общий курс физики т. II, 2005, с. 90.

[FOOTNOTEБазаров_И._П.,_Термодинамика201058-35] Базаров И. П., Термодинамика, 2010, с. 58.

[FOOTNOTEБазаров_И._П.,_Термодинамика201075-36] Базаров И. П., Термодинамика, 2010, с. 75.

[FOOTNOTEШамбадаль&nbsp;_П.,&nbsp;_Развитие&nbsp;и&nbsp;_приложение&nbsp;энтропии196761—64-37] Шамбадаль П., Развитие и приложение энтропии, 1967, с. 61—64.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,Термодинамика1954197—198-38] Белоконь Н. И.,Термодинамика, 1954, с. 197—198.

[FOOTNOTEГухман&nbsp;А.&nbsp;А.,_Об&nbsp;основаниях&nbsp;термодинамики2010370-39] Гухман А. А., Об основаниях термодинамики, 2010, с. 370.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,Термодинамика1954244-40] Белоконь Н. И.,Термодинамика, 1954, с. 244.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,Термодинамика1954245—246-41] Белоконь Н. И.,Термодинамика, 1954, с. 245—246.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,&nbsp;Основные&nbsp;принципы&nbsp;термодинамики196855—56-42] Белоконь Н. И., Основные принципы термодинамики, 1968, с. 55—56.

[FOOTNOTEБелоконь&nbsp;Н.&nbsp;И.,Термодинамика1954166—184-43] Белоконь Н. И.,Термодинамика, 1954, с. 166—184.

[FOOTNOTEГухман&nbsp;А.&nbsp;А.,_Об&nbsp;основаниях&nbsp;термодинамики2010351-44] Гухман А. А., Об основаниях термодинамики, 2010, с. 351.

[FOOTNOTEАфанасьева-Эренфест&nbsp;Т.&nbsp;А.,_Необратимость,&nbsp;односторонность&nbsp;и&nbsp;второе&nbsp;начало&nbsp;термодинамики19283-45] Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928, с. 3.

[FOOTNOTEАфанасьева-Эренфест&nbsp;Т.&nbsp;А.,_Необратимость,&nbsp;односторонность&nbsp;и&nbsp;второе&nbsp;начало&nbsp;термодинамики192826—27-46] Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928, с. 26—27.

[FOOTNOTEБазаров_И._П.,_Термодинамика201082─84.-47] Базаров И. П., Термодинамика, 2010, с. 82─84..