Функтор Ext
В математиці, функтор Ext є похідним функтором функтора Hom. Разом із функтором Tor, Ext є одним із головних понять гомологічної алгебри. За допомогою цього функтора можна дати означення когомології груп, когомології алгебр Лі і когомології Хохшильда.
У випадку абелевих груп, Ext був введений Рейнхольдом Бером у 1934 році. Термін Ext був запропонований у 1942 році Ейленбергом і МакЛейном, які застосували це поняття у топології. Для модулів над довільним кільцем, означення функтора Ext було дане Картаном і Ейленбергом у 1956 році в книзі Homological Algebra.[1]
Означення
Нехай R — кільце і R-Mod позначає категорію модулів над R. (Для некомутативних кілець це може бути категорія лівих R-модулів чи правих R-модулів.) Для деякого R-модуля A, позначимо T(B) = HomR(A, B) де B належить категорії R-Mod. Цей функтор є точним зліва функтором із категорії R-Mod у категорію абелевих груп Ab, і тому для нього існує правий похідний функтор RiT. Групами Ext є абелеві групи за означенням рівні
для цілих чисел i.
Більш детально, нехай маємо деяку ін'єктивну резольвенту:
Відкинемо в ній елемент B, і утворимо коланцюговий комплекс:
Для кожного цілого числа i, ExtiR(A, B) є когомологією цього комплексу по порядку i. Для від'ємних i когомологія вважається рівною нулю. Наприклад, Ext0R(A, B) є ядром відображення HomR(A, I0) → HomR(A, I1), яке є ізоморфним HomR(A, B).
Еквівалентне означення використовує функтор G(A)=HomR(A, B), для деякого R-модуля B. У даному випадку маємо контраваріантний функтор, який можна розглядати як точний зліва функтор із оберненої категорії (R-Mod)op у категорію Ab. Групи Ext за означеннями є похідними функторами RiG:
В цьому випадку спершу вводиться проєктивна резольвента
Після вилучення A і утворення коланцюгового комплекса:
можна означити ExtiR(A, B) як когомологію цього комплексу в позиції i.
Описані вище побудови не залежать від вибору проєктивної чи ін'єктивної резольвенти і у всіх випадках отримуються однакові групи.[2]
Для комутативного кільця R і R-модулів A і B, ExtiR(A, B) є R-модулем (використовуючи те, що HomR(A, B) є R-модулем у цьому випадку). Для некомутативного кільця R, ExtiR(A, B) є загалом лише абелевою групою. Якщо R є алгеброю над кільцем S (що, зокрема, означає, що S є комутативним кільцем), тоді ExtiR(A, B) є принаймні S-модулем.
Властивості Ext
- Ext0R(A, B) ≅ HomR(A, B).
- ExtiR(A, B) = 0 для всіх i > 0 якщо R-модуль A є проєктивним (наприклад, вільним) або якщо B є ін'єктивним.
- виконуються і обернені твердження:
- Якщо Ext1R(A, B) = 0 для всіх B, тоді A є проєктивним (і тому ExtiR(A, B) = 0 для всіх i > 0).
- Якщо Ext1R(A, B) = 0 для всіх A, тоді B є ін'єктивним (і тому ExtiR(A, B) = 0 для всіх i > 0).
- для всіх i ≥ 2 і всіх абелевих груп A і B.[3]
- Якщо R є комутативним кільцем і елемент u не є дільником нуля, тоді
- для кожного R-модуля B. Тут B[u] позначає підгрупу у B, задану як {x ∈ B: ux = 0}. Якщо R є кільцем цілих чисел за допомогою цих обчислень можна порахувати для будь-якої скінченнопородженої абелевої групи A.
- Згідно загальних властивостей похідних функторів, для Ext існують дві основні довгі точні послідовності.[4] Спершу, коротка точна послідовність 0 → K → L → M → 0 R-модулів породжує довгу точну послідовність виду
- для будь-якого R-модуля A. Також, коротка точна послідовність 0 → K → L → M → 0 породжує довгу точну послідовність
- для будь-якого R-модуля B.
- Ext відображає прямі суми (можливо нескінченні) по першій змінній і прямі добутки по другій змінній у прямі добутки.[5] Тобто,
- Нехай A скінченнопороджений модуль над комутативним нетеровим кільцем R. Тоді Ext комутує із операцією локалізації, тобто для кожної мультиплікативно замкнутої множини S у R, довільного R-модуля B і цілого числа i,[6]
Ext і розширення
Еквівалентність розширень
Назва Ext походить від зв'язку із розширеннями модулів. Для R-модулів A і B, розширенням A за допомогою B називається коротка точна послідовність R-модулів
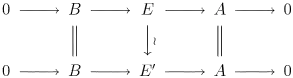
Два розширення
називаються еквівалентними (як розширення A за допомогою B) якщо існує комутативна діаграма
Середня стрілка при цьому є ізоморфізмом. Розширення A за допомогою B розщеплюється якщо воно є еквівалентним тривіальному розширенню
Існує бієкція між класами еквівалентності розширень A за допомогою B і елементами Ext0R(A, B).[7] При цій бієкції тривіальні розширення відповідають нульовим елементам груп Ext1R(A, B).
Суми Бера розширень
Сума Бера є описом абелевої структури Ext1R(A, B), якщо її розглядати як клас еквівалентності розширення A за допомогою B.[8] А саме, для двох розширень
і
спершу розглядається розшарований добуток над ,
Тоді можна взяти фактор-модуль
Сумою Бера E і E′ є розширення
де першим відображенням є а другим .
Сума Бера є визначеною з точністю до еквівалентності, комутативною і нейтральним елементом є тривіальне розширення. Оберненим розширенням до розширення 0 → B → E → A → 0 є розширення із тим самим модулем E але із заміною гомоморфізму E → A на від'ємний.
Побудова Ext для абелевих категорій
Нобуо Йонеда ввів абелеві групи ExtnC(A, B) для об'єктів A і B в довільній абелевій категорії C; його означення узгоджується із означення в термінах резольвент якщо C має достатньо проєктивних чи ін'єктивних об'єктів. Спершу, Ext0R(A,B) = HomC(A, B). Далі, Ext1C(A, B) є множиною класів еквівалентності розширення A за допомогою B, що є абелевою групою відносно суми Бера. Нарешті, групи Ext вищих порядків ExtnC(A, B) за означенням є класами еквівалентності n-розширень, тобто точними послідовностями
згідно відношення еквівалентності породженого рівностями між розширеннями виду
якщо існують відображення Xm → X′m для всіх m із {1, 2, ..., n} такі, що всі відповідні квадрати комутують, тобто якщо існує ланцюгове відображення ξ → ξ', що є рівним одиничному на A і B.
Сума Бера таких двох n-розширень утворюються введенням як розшарованого добутку і над A, і як розшарованого кодобутку і під B.[9] Тоді сума Бера розширень є рівною
Важливі окремі випадки
- Когомологія груп є рівною , де G є групою, M є представлення G над цілими числами, і є груповим кільцем G.
- Для алгебри A над кільцем k і A-бімодуля M, когомологія Хохшильда є рівною
- Когомологія алгебр Лі є рівною , де є алгеброю Лі над комутативним кільцем k, M є -модуль, і є універсальною обгортуючою алгеброю.
- Для топологічного простору X, когомологія пучків є рівною Тут Ext розглядається у абелевій категорії пучків абелевих груп на X, і є пучком локально сталих функцій із значенням у (із дискретною топологією).
- Для локального кільця Нетер R із полем лишків k, має структуру кокомутативної градуйованої алгебри Хопфа над k. Коли характеристика k є рівною 0, то ця алгебра є універсальною обгортуючою алгеброю когомології Андре — Квіллена D*(k/R,k) (що є градуйованою алгеброю Лі).[10]
Див. також
Примітки
- Weibel (1999); Cartan & Eilenberg (1956), section VI.1.
- Weibel (1994), sections 2.4 і 2.5 і Theorem 2.7.6.
- Weibeil (1994), Lemma 3.3.1.
- Weibel (1994), означення 2.1.1.
- Weibel (1994), Proposition 3.3.4.
- Weibel (1994), Lemma 3.3.8.
- Weibel (1994), Theorem 3.4.3.
- Weibel (1994), Corollary 3.4.5.
- Weibel (1994), Vists 3.4.6. Some minor corrections is in errata.
- Quillen (1970), section 7.
Література
- Baer, Reinhold (1934). Erweiterung von Gruppen und ihren Isomorphismen. Mathematische Zeitschrift. 38(1): 375–416. Zbl 0009.01101. doi:10.1007/BF01170643.
- Cartan, Henri; Eilenberg, Samuel (1999) [1956]. Homological algebra. Princeton: Princeton University Press. ISBN 0-691-04991-2. MR 0077480.
- Eilenberg, Samuel; MacLane, Saunders (1942). Group extensions and homology. Annals of Mathematics 43: 757—931. MR 0007108.
- Quillen, Daniel (1970). On the (co-)homology of commutative rings. Applications of categorical algebra. Proc. Symp. Pure Mat. 17. American Mathematical Society. с. 65–87. MR 0257068.
- Weibel, Charles A (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324.
- Weibel, Charles A. (1999). History of homological algebra. History of topology. Amsterdam: North-Holland. с. 797—836. MR 1721123.