Невласний інтеграл
Невла́сний інтегра́л, невласти́вий інтегра́л — розширення поняття інтеграла Рімана. В інтегралі Рімана розглядають
- скінченний проміжок інтегрування [a, b];
- підінтегральна функція f(x) — обмежена (необхідна умова інтегровності функції за Ріманом).
| Розділи в | ||||||
| Математичному аналізі | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
||||||
|
||||||
|
||||||
|
Спеціалізовані |
||||||
Невласний інтеграл I (першого) роду розглядається на нескінченному проміжку інтегрування (і обчислюється як границя послідовності інтегралів Рімана по скінченних проміжках, які «розширюються»), а невласний інтеграл II (другого) роду — це інтеграл з необмеженою підінтегровною функцією (обчислюється як границя послідовності інтегралів Рімана по інтервалах, які наближаються до особливої точки підінтегральної функції, де ця функція прямує до нескінченності).
Подальшим узагальненням інтеграла Рімана є поняття головного значення інтеграла за Коші.
Невласний інтеграл першого роду («нескінченний інтервал»)
Означення
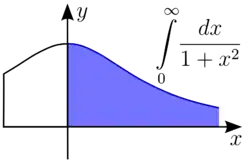
Нехай a ∈ R. Невласний інтеграл першого роду визначається на одному з таких нескінченних інтервалів:
- (a, +∞);
- (−∞, a);
- (-∞, +∞).
Означення для інтервалу (a, +∞)
Означення. Нехай функція f : (a, +∞) → R така, що ∀ A > a : f ∈ R([a, A]), тобто є скінченним інтеграл Рімана
Якщо існує скінченна границя послідовності інтегралів F(A), коли A → +∞, то
- значення цієї границі називають невласним інтегралом першого роду для функції f по інтервалу (a, +∞) і позначають символом
- невласний інтеграл називають збіжним.
Якщо ж виконуються умови означення, але границя F(A) не існує або рівна ±∞, то кажуть, що невласний інтеграл першого роду для функції f розбігається (або є розбіжним).
Аналогічно можна дати означення невласного інтеграла першого роду для інтервалу (−∞, a).
Приклад. Розглянемо інтеграл
Для довільного A > 0 функція f(x) = 1/x ∉ R([-1, A]) (бо є необмеженою в околі точки 0). Отже, даний інтеграл не є невласним інтегралом першого роду.
Приклад. Розглянемо інтеграл
Для всіх A > 0 функція f(x) = 1/(1+x²) ∈ R([0, A]) як обмежена функція. Отже, даний інтеграл є невласним інтегралом першого роду. Дослідимо його збіжність:
Отже, даний невласний інтеграл є збіжним, і його значення дорівнює π/2.
Приклад. Розглянемо інтеграл
Для всіх A > 1 функція f(x) = 1/x ∈ R([1, A]) як обмежена функція. Отже, даний інтеграл є невласним інтегралом першого роду. Дослідимо його збіжність:
Отже, даний невласний інтеграл є розбіжним.
Приклад. Розглянемо інтеграл
Для всіх A > 0 функція f(x) = cos x ∈ R([0, A]) як обмежена функція. Отже, даний інтеграл є невласним інтегралом першого роду. Дослідимо його збіжність:
Оскільки не існує границі sin A при A → +∞,[1] то даний невласний інтеграл є розбіжним.
Означення для інтервалу (−∞, +∞)
Означення. Нехай функція f : (−∞, +∞) → R така, що ∀ A, B ∈ R, A < B : f ∈ R([A, B]), тобто є скінченним інтеграл Рімана
Якщо існує скінченна подвійна границя послідовності інтегралів F(A, B), коли A → −∞ та B → +∞ незалежно одне від одного, то
- значення цієї границі називають невласним інтегралом першого роду для функції f по інтервалу (−∞, +∞) і позначають одним із символів
- невласний інтеграл називають збіжним.
Якщо ж виконується умова означення, але границя F(A, B) не існує або рівна ±∞, то кажуть, що невласний інтеграл першого роду для функції f розбігається (або є розбіжним).
Властивості
- збігається ⇔ ∀a ∈ R інтеграли є збіжними;
- розбігається ⇔ ∃a ∈ R таке, що хоча б один із інтегралів
є розбіжним.
Критерій Коші збіжності невласного інтеграла першого роду
Нехай функція f(x) задовольняє умові означення для інтервалу (a, +∞).
Невласний інтеграл збігається тоді і лише тоді, коли
Аналогічно можна сформулювати критерій Коші збіжності невласного інтеграла першого роду по інтервалу (−∞, a).
Ознаки порівняння збіжності невласних інтегралів першого роду
Нехай функція f(x) задовольняє умові означення для інтервалу (a, +∞).
- Якщо існує функція g(x) така, що
- |f(x)| ≤ g(x) для всіх x ≥ a та
- ∫a+∞g(x) dx збігається,
то ∫a+∞f(x) dx теж збігається.
- Якщо існує функція g(x) така, що
- 0 ≤ g(x) ≤ |f(x)| для всіх x ≥ a та
- ∫a+∞g(x) dx розбігається,
то ∫a+∞f(x) dx теж розбігається.
У випадку, коли f(x) — невід'ємна, ознаки порівняння можна схематично записати у вигляді:
f(x) ≤ g(x)
зб. ⇐ зб.
розб. ⇒ розб.
Аналогічні твердження мають місце для невласних інтегралів по інтервалам (−∞, a) та (−∞, +∞).
Абсолютна збіжність
Означення. Невласний інтеграл називається абсолютно збіжним, якщо збіжним є невласний інтеграл
Означення. Збіжний невласний інтеграл, який не є абсолютно збіжним, називається умовно збіжним.
Теорема. Якщо невласний інтеграл збігається абсолютно, то він збігається.
Ознака Діріхле
Нехай для функцій {f, g} ⊂ C([a, +∞)) виконуються умови:
- існує стала C ∈ R така, що для всіх A ≥ a:
- функція g монотонна на [a, +∞);
- g(x) → 0 при x → +∞.
Тоді збіжним буде невласний інтеграл
Приклад. Розглянемо інтеграл Діріхле
Цей інтеграл є збіжним за ознакою Діріхле: функції f(x) = sin x та g(x) = 1/x є неперервними на [1, +∞) та задовольняють умовам 1—3 ознаки Діріхле.
Ознака Абеля
Нехай функції f, g визначені на [a, +∞) та задовольняють умовам:
- збіжним є невласний інтеграл
- функція g монотонна на [a, +∞);
- функція g — обмежена на [a, +∞).
Тоді збіжним буде невласний інтеграл
Невласний інтеграл другого роду («від необмеженої функції»)
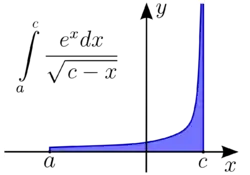
Невласний інтеграл другого роду є узагальненням інтеграла Рімана для випадку необмеженої функції.
Нехай функція f(x) визначена та неперервна на інтервалі [a, b).
Означення. Точка b називається особливою точкою функції f(x), якщо
- для всіх α ∈ (0, b − a) функція f є обмеженою на інтервалі [a, b − α);
- функція f — необмежена на інтервалі [a, b).
Розглянемо функцію
Означення. Нехай виконуються умови:
- функція f(x) визначена та неперервна на інтервалі [a, b);
- точка b — особлива точка функції f(x);
- існує скінченна границя F(α) при α → 0.
Тоді
- значення цієї границі називають невласним інтегралом другого роду і позначають символом
- кажуть, що цей невласний інтеграл збігається (або є збіжним).
Якщо виконуються умови 1—2 означення, але границя F(α) не існує або дорівнює ±∞, то такий невласний інтеграл розбігається (називається розбіжним).
Зауваження. У випадку, коли функція f(x) має скінченну кількість особливих точок на проміжку інтегрування, то інтеграл розбивають на суму інтегралів по інтервалам, в кожному з яких присутня лише одна особлива точка на одному з кінців інтегрування.
Зв'язок між невласними інтегралами І та ІІ родів
Нижче наведено відображення, які пов'язують інтервали скінченної на нескінченної довжин:
x заміна змінної t I [a, +∞) → x = a/(1−t) → [0, 1) II [a, b) → x = b − (b−a)/(1−t) → [0, +∞)
У невласному інтегралі першого роду виконаємо заміну змінних згідно рядку I:
в результаті чого отримаємо інтеграл по скінченному проміжку [0, 1] від необмеженої функції, тобто невласний інтеграл другого роду.
І навпаки, виконавши заміну в невласному інтегралі другого роду згідно рядку ІІ
отримаємо невласний інтеграл першого роду по нескінченному проміжку [0, +∞).
Зауваження. Зв'язок між невласними інтегралами І та ІІ родів дозволяє звести питання про збіжність невласного інтеграла ІІ роду до питання про збіжність невласного інтеграла І роду, а саме: невласний інтеграл ІІ роду збігається тоді і лише тоді, коли збігається відповідний невласний інтеграл І роду.
Інтеграл від необмеженої функції по нескінченному проміжку
Розглянемо інтеграл
в якому підінтегральна функція f(x) має скінченну кількість особливих точок p1 < p2 < … < pn всередині проміжку інтегрування. Щоб обчислити даний інтеграл, потрібно скористатися рівністю
В правій частині цієї рівності перший інтеграл — це інтеграл по скінченному проміжку інтегрування зі скінченною кількістю полюсів (див. Зауваження в розділі Невласний інтеграл другого роду («від необмеженої функції»)), а другий інтеграл — це невласний інтеграл першого роду (якщо f(x) задовольняє умові означення для інтервалу (a, +∞)). ).
Гамма-функція та бета-функція
Виділяють особливий клас функцій, які представлені у вигляді власного або невласного інтеграла, який залежить не тільки від формальної змінної, а і від параметра. Такі функції називаються інтегралами, залежними від параметра. До їх числа відносяться гамма-функція та бета-функція Ейлера.
Гамма функція представляється невласним інтегралом першого роду:
Бета функція є невласним інтегралом другого роду:
Див. також
- Невизначений інтеграл функції комплексної змінної
- Первісна
- Інтегральне числення
- Визначений інтеграл
- Інтеграл Рімана
- Інтеграл Стілтьєса (або інтеграл Рімана—Стілтьєса)
- Інтеграл Лебега
- Інтеграл Даніелла
- Інтеграл Бохнера
- Головне значення інтеграла за Коші
- Визначений інтеграл
- Метод Самокиша — чисельний метод для обчислення інтегралів з особливостями.
Примітки
- Розглянемо дві послідовності Ak = 2πk та A´k = π/2 + 2πk, k ≥ 1,. Маємо sin Ak → 0, a sin A´k → 1 при k → +∞.
Джерела
- Дороговцев А. Я. Математический анализ. — Київ, Вища школа, 1985.
Посилання
- Невласні інтеграли // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 453. — 594 с.