Фазовий портрет
Фазовий портрет - зображення траєкторій динамічної системи у фазовому просторі.
| Диференціальні рівняння |
|---|
 |
|
Види рівнянь
|
|
Методи розв'язання
|
|
Відомі рівняння
|
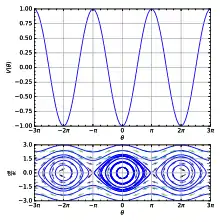
Фазовий портрет математичного маятника. Верхня крива - залежність кута від часу в коливальному режимі
Кожен стан системи відповідає певній точці на фазовому портреті. Фазові портрети служать для наочного відображення особливостей еволюції динамічної системи: стаціонарних точок, циклів, басейнів притягання.
Для двовимірної системи фазовий портрет повністю відображає типи траєкторій, які можуть реалізуватися. Для системи більшої вимірності будуються проєкції фазових траєкторій на вибрану площину фазового простору.
Приклади
На малюнку праворуч показаний фазовий портрет математичного маятника, тобто залежність кутової швидкості від кута повороту. На фазовому портреті можна помітити різні типи траєкторій:
- Непорушна центральна точка в колах відповідає стану спокою (точка рівноваги)
- Точки перехрещення відповідають положенню нестійкої рівноваги (маятник стоїть вертикально).
- Концентричні лінії навколо точок рівноваги (цикли) відповідають коливанням. При коливаннях кутова швидкість змінює знак, а кут змінюється в певних межах.
- Обертання відображене верхніми й нижніми хвилястими лініями. При обертанні кутова швидкість змінюється мало, а кут росте або зменшується необмежено.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.