Перелік об'єктів, названих на честь Леонарда Ейлера
Леона́рд Е́йлер (нім. Leonhard Euler) вважається найвидатнішим математиком 18-го століття, а, можливо, навіть усіх часів. Він також є одним із найплідніших — збірка всіх його творів зайняла б 60-80 томів[1].
Ейлер є автором 866 наукових публікацій, зокрема у галузях математичного аналізу, диференціальної геометрії, теорії чисел, теорії графів, наближених обчислень, небесної механіки, математичної фізики, оптики, балістики, кораблебудуванні, теорії музики, що мали значний вплив на розвиток науки. Саме він ввів більшість математичних понять та символів у сучасну математику, наприклад: f(x), e, π (пі), уявна одиниця i, символ суми ∑ і багато інших.
Існує безліч математичних та фізичних об'єктів, названих на честь Леонарда Ейлера:
Теореми
- Теорема Ейлера (теорія чисел) — узагальнення малої теореми Ферма.
- Теорема обертання Ейлера — твердження, що будь-яке тривимірне обертання має вісь.
- Теорема Ейлера (планиметрия) — залежність між радіусами вписаного та описаного кіл трикутника.
- Дві теореми Ейлера,пентагональні теорема Ейлера (комбінаторика).
- Гіпотеза Ейлера (теорія чисел) — твердження, що для будь-якого натурального числа ніяку n-ю ступінь натурального числа не можна представити у вигляді суми з натуральних чисел, зведених в -ю ступінь. Спростовано.
- Теорема Ейлера для багатогранників — зв'язок між числом вершин, ребер та граней багатогранника. Також має сенс для планарного графу.
Лема
- Лема Ейлера — властивість однорідних функцій.
Рівняння
- Рівняння Ейлера — Лагранжа — основні формули варіаційного числення, c допомогою яких шукаються екстремуми функціоналів, що залежать від невідомої функції та її похідної.
- Рівняння Ейлера — Пуассона — узагальнення рівняння Ейлера — Лагранжа на випадок, коли функціонал залежить від невідомої функції та її похідних вище першого порядку.
- Рівняння Ейлера (механіка) (механіка твердого тіла) — описують обертання твердого тіла.
- Рівняння Коші-Ейлера — лінійне однорідне звичайне диференціальне рівняння зі змінними коефіцієнтами.
- Рівняння Ейлера (гідродинаміка) — описує рух ідеальної (нев'язкої) стисливої рідини чи газу.
- Ейлерові точки лібрації (колінеарні точки).
- Рівняння Ейлера — Бернуллі — описує рівновагу балки.
Функції
- Функція Ейлера — кількість натуральних чисел, що не перевершують та взаємно простих з ним.
- Функція Ейлера (комплексний аналіз) — модулярна функція Є класичним прикладом, що показує зв'язок між комбінаторикою та комплексним аналізом.
Тотожності
- Тотожність Ейлера в теорії чисел
- Тотожність Ейлера (комплексний аналіз) — окремий випадок формули Ейлера, що зв'язує п'ять фундаментальних чисел математики.
- Тотожність Ейлера (кватерніони), «тотожність Ейлера про чотири квадратах» (алгебра) — теорема про те, що добуток сум чотирьох квадратів є сумою чотирьох квадратів.
- Тотожність Ейлера (алгебра многочленів) — співвідношення яке справедливо для будь алгебраїчної форми (однорідного многочлена) ступеня
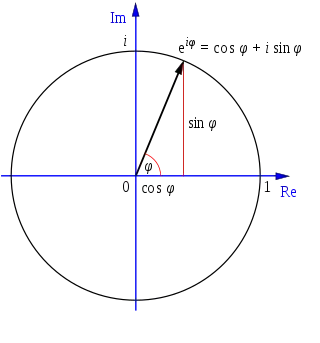
Геометрична інтерпретація Формули Ейлера
Формули
- Формула Ейлера (комплексний аналіз) : , пов'язує комплексну експоненту з тригонометричними функціями.
- Формула Ейлера (кінематика твердого тіла) — , пов'язує швидкості двох точок твердого тіла.
- Формула Ейлера в геометрії трикутника — вираз для відстані між інцентром та центром описаного кола трикутника, див. інцентр.
- Формула Ейлера в геометрії чотирикутника — вираз для відстані між серединами діагоналей — його квадрат, помножений на 4, дорівнює сумі квадратів сторін чотирикутника мінус суму квадратів його діагоналей. Як окремий випадок, з неї можна отримати: тотожність паралелограма, довжину медіани трикутника.
- Формула Ейлера для суми перших n членів гармонійного ряду.
- Формула Ейлера в теорії графів: зв'язує кількість вершин, ребер та граней планарного графу.
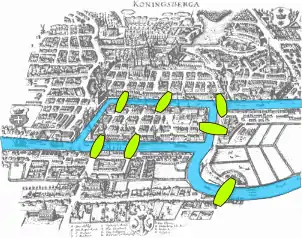
Карта Кенігсберга в часи Ейлера показує фактичне розташування сімох мостів, виділяючи на річку Преголя та мости.
Інтеграли
- Бета-функція — ейлерів інтеграл (інтеграл Ейлера) першого роду.
- Гамма-функція — ейлерів інтеграл (інтеграл Ейлера) другого роду.
- Інтеграл Ейлера — Пуассона (т. зв. гаусів інтеграл).
Числа
- Постійна Ейлера — Маськероні — межа різниці між частковою сумою гармонійного ряду та натуральним логарифмом числа.
- E (число) — підставу натурального логарифма, ірраціональне та трансцендентне число e.
- Число Ейлера (фізика) — безрозмірний коефіцієнт, що має місце в рівняннях Нав'є — Стокса, що описує відношення між силами тиску на одиничний об'єм рідини (або газу) та інерційними силами.
- Числа Ейлера I роду
- Зручне число
- Щасливе число Ейлера
- Ціле число Ейлера (Ціле число Ейзенштейна)
Інше

1,2-метровий рефлектор Леонард Ейлер обсерваторії Ла-Силья
- Кути Ейлера — узагальнені координати при обертанні навколо нерухомої точки.
- Багаточлени Ейлера.
- Перетворення Ейлера — інтегральне перетворення.
- Пряма Ейлера (геометрія трикутника) — пряма, що проходить через центр описаного кола та ортоцентр трикутника.
- Коло Ейлера, «коло дев'яти точок» — в геометрії трикутника коло, що проходить через середини всіх трьох сторін трикутника.
- Кола Ейлера — геометрична схема для відображення відносини між підмножинами.
- Ейлерів цикл, ейлерів ланцюг (теорія графів) — шлях у графі, проходить по всіх ребрах графу та притому лише по одному разу.
- Ейлерів сплайн — періодичний ідеальний сплайн мінімальної норми.
- Ейлерова сила — в механіці, така сила, яка при стисканні стрижня викличе втрату його стійкості (поздовжній вигин).
- Ейлер — кратер ударного походження на видимій частині Місяця, діаметр 28 км.
- Медаль (англ. Euler Medal), з 1993 щорічно присуджується канадським Інститутом комбінаторики та її додатків (англ. Institute of Combinatorics and its Applications) за досягнення в цій галузі математики.
- Золота медаль імені Леонарда Ейлера Академії наук СРСР та Російської академії наук.
- Підстановки Ейлера — підстановка, за допомогою якої вирішуються деякі види інтегралів.
- Проєкт Ейлер — проект в Інтернеті, що об'єднує сотні тисяч любителів математики та програмування.
Див. також
- Перелік об'єктів, названих на честь Ісаака Ньютона
- Перелік об'єктів, названих на честь Лагранжа
- Перелік об'єктів, названих на честь Лейбніца
Примітки
- Finkel, B.F. (1897). Biography- Leonard Euler. The American Mathematical Monthly 4 (12): 300. doi:10.2307/2968971.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.